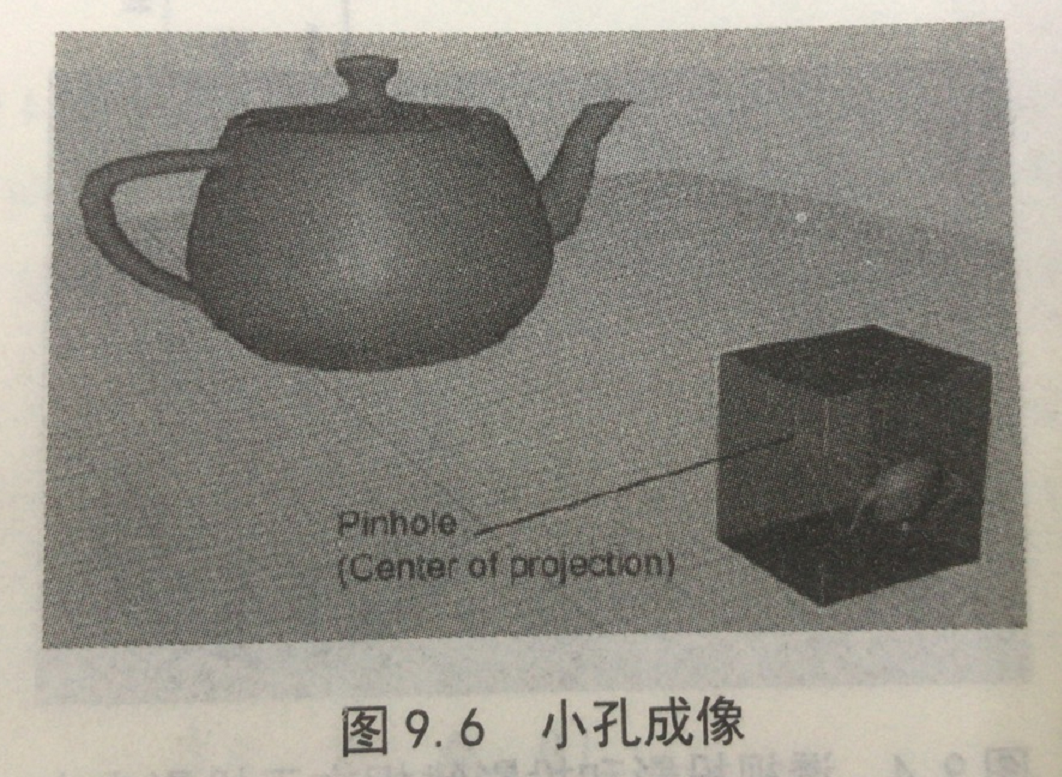
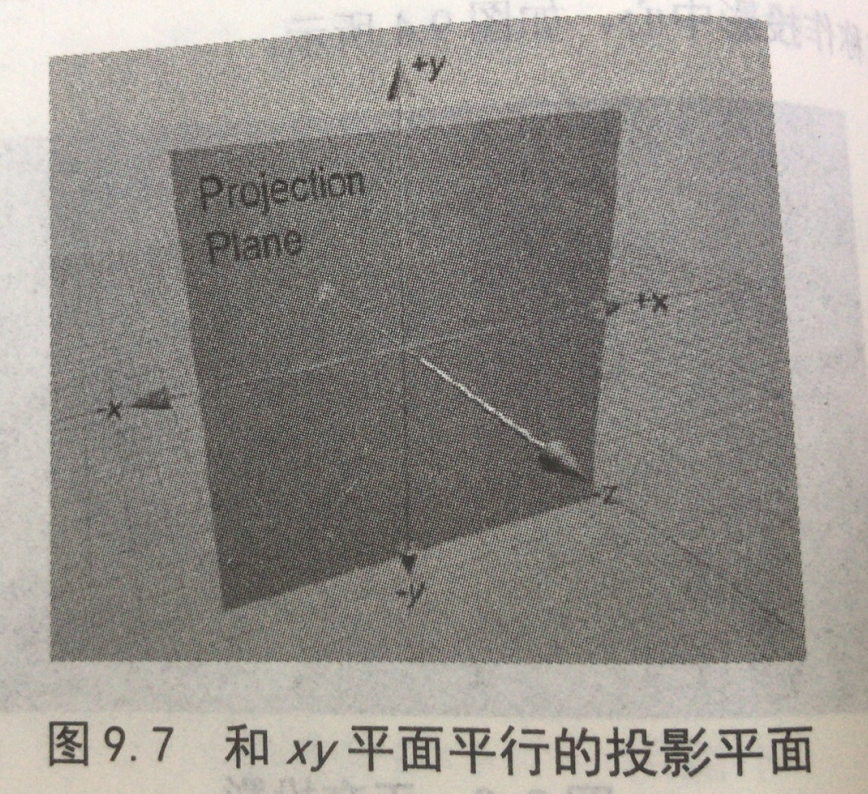
一、齐次坐标（Homogeneous coordinates）

单词Homogeneous的中文意思是同质的，同种类的。就是说有一些坐标虽然数值上不同，但描述的是同一个坐标！这有啥用？在投影中，我们知道，两个不同位置的物体的投影是完全有可能重叠在一块的，这就是齐次坐标的使用场景。
在数学里，齐次坐标也叫投影坐标（projective coordinates），它是指一个用于投影几何里的坐标系统。
下图描述的是定义于齐次坐标内的多项式曲线（蓝色），以及于平面上的投影（有理曲线，红色）。

简单理解齐次坐标就是，用n+1维向量来表示n维向量，目的是可以用n+1维的线性变换来表达n维的仿射变换。线性变换就是，仿射变换就是。所有这样做可以将所有的变换都集中到一个矩阵中，简化计算过程。
3D中的正交投影和透视投影变换效果，就可以通过一个矩阵来表达。

这样，我们就可以通过计算4阶矩阵来实现3D的各种仿射变换。得到的齐次坐标结果只需要将各分量除以即可“降维”回3D坐标。
同理。

二、透视投影（Perspective Projection）

• 正交投影（Ortho Projection）
  • 也叫平行投影，投影线是平行的。
  • 物体靠近/远离投影平面，物体大小不会变化。

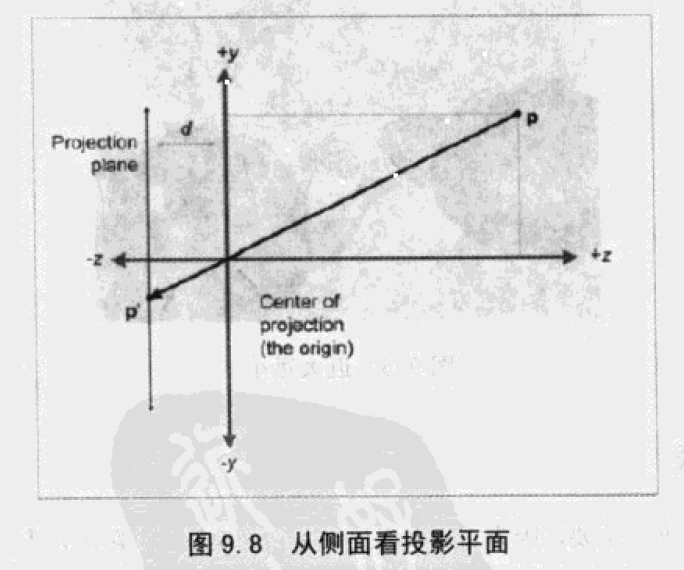
• 透视投影
  

  • 投影线不再平行，而是会相交于一点，该点称为投影中心。
    • 类比小孔成像投影中心就是“小孔位置”。
    • 投影中心如果在投影平面的前面（投影中心在投影平面、物体之间），则投影将是倒立的。

  • 近大远小

    • 离投影平面近的物体，投影更大，反之更小。
    • 称为透视缩略，是非常重要的视觉现象，符合人类视觉系统模型。
    • 这是在2D投影平面上实现3D视觉效果的根本所在。

      1、小孔成像**

      

  • 盒子靠近茶壶的一侧，有一个小孔（投影中心）

  • 光线透过小孔照射到另一侧背面，形成投影平面
  • 盒子的左右透明

    2、几何原型

    
    
    
    。

由相似三角形得到：

在实际应用中，负号会带来不必要的计算复杂性，将投影平面移到投影中心的前面（），虽然小孔成像中不存在，但上面的数学公式依然成立。

3、总结

• 乘以投影矩阵并不是进行实际的投影变换，看上面结果可知，还需要结果向量再除以分量。
• 公式不能应对所有情况，比如。
• 都已经有直接的坐标计算公式了，为什么还要麻烦的转成4x4矩阵？
  • 1、4x4矩阵完美的将投影表达为了变换，这样可以和其他变换完美“兼容”和配合。
  • 2、使得投影到不平行于坐标轴的投影平面变得可行。
• 实际应用中的投影矩阵并没有那么简单，还有很多需要考虑。

  三、投影矩阵计算

  语雀内容