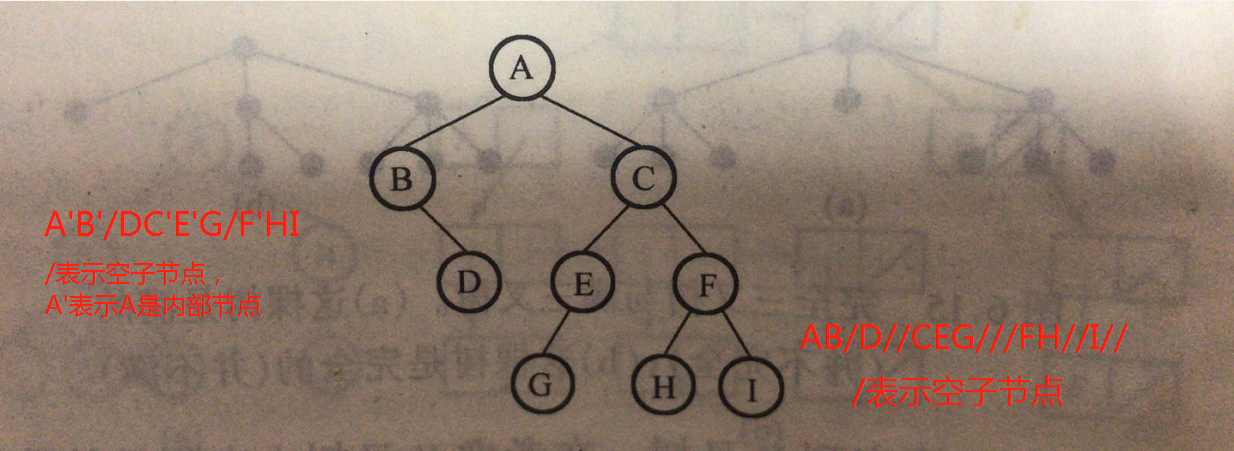
一、二叉树

涉及到树，一定要想到树的深度，一般越小越好。
点击查看【processon】
满二叉树：每个节点都有0或2个子节点。
完全二叉树：
1、从根节点起每层必须左到右填充。
2、高度为d，除了d-1层以外，每次都是满的。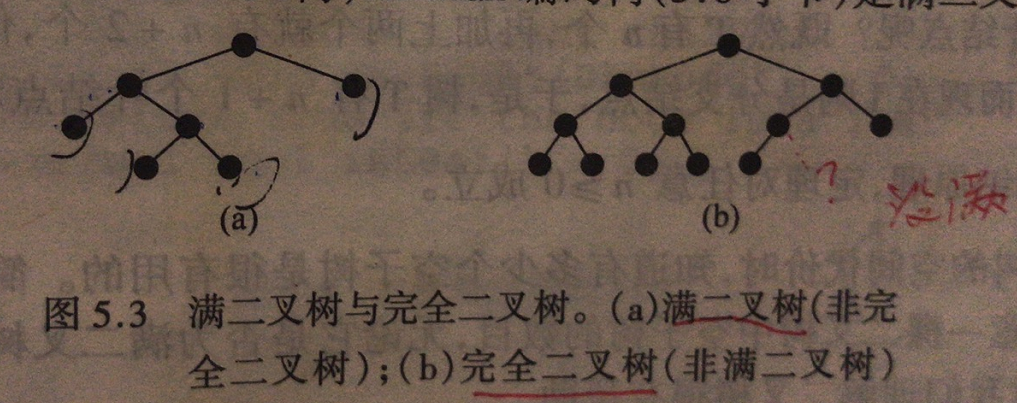

满二叉树定理：非空满二叉树，叶节点 = 内部节点 + 1。
二叉树定理：非空二叉树，空子树 = 节点数 + 1。

二叉树节点ADT

template<class Elem> class BinNode{
public:
    virtual Elem& val() = 0;
    virtual void setVal(const Elem&) = 0;
    virtual BinNode* left() const = 0;
    virtual BinNode* right() const = 0;
    virtual void setLeft(BinNode *) = 0;
    virtual void setRight(BinNode *) = 0;
    virtual bool isLeaf() = 0;
}

1、周游（遍历）二叉树

前序遍历：根 -> 左 -> 右。
后序遍历：左 -> 右 -> 根。
中序遍历：左 -> 根 -> 右。
C++代码实现：

//前序遍历
template<class Elem>
void preorder(BinNode<Elem>* root){
    if(root == NULL) return;
    visit(root);
    preorder(root->left());
    preorder(root->right());
}

//计算节点数
template<class Elem>
void count(BinNode<Elem>* root){
    if(root == NULL) return 0;
    return 1 + count(root->left()) + count(root->right());
}

2、二叉树实现

二叉树实现（指针）

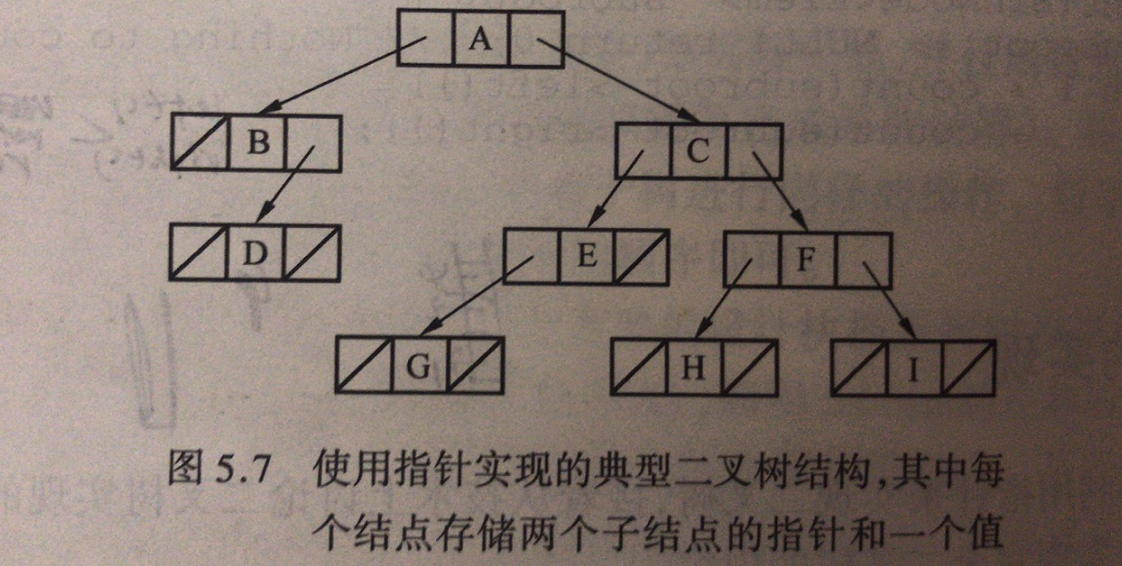
template<class Elem>
class BinNodePtr : public BinNode<Elem>{
private:
    Elem val;
    BinNodePtr* left;
    BinNodePtr* right;
public:
    BinNodePtr(){
        left = right = NULL;
    }
    BinNodePtr(const Elem* elem, BinNodePtr* l = NULL, BinNodePtr* r = NULL){
        it = elem;
        left = l;
        right = r;
    }
    ~BinNodePtr(){};
    Elem& val(){
        return val;
    }
    void setVal(const Elem& elem){
        val = elem;
    }
    BinNode* left() const{
        return left;
    }
    BinNode* right() const{
        return right;
    }
    void setLeft(BinNode * l){
        left = (BinNodePtr*) l;
    }
    void setRight(BinNode * r){
        right = (BinNodePtr*) r;
    }
    bool isLeaf(){
        return (left == NULL) && (right == NULL);
    }
}

弊端（分支、叶节点不分）

分支节点和叶节点是两种节点。根据二叉树的实际应用经验，叶节点和分支节点的作用有很大不同，比如可能只有叶节点存储数据，可能两种节点存储的数据不同。所以分支节点和叶节点需要分开定义。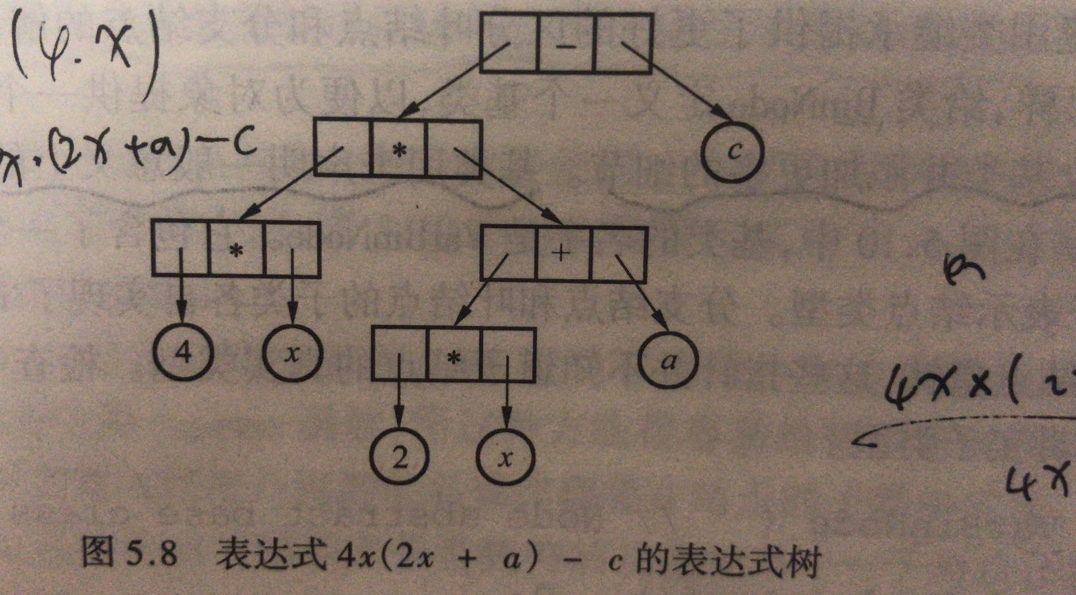

class VarBinNode{
public:
    virtual bool isLeaf() = 0;
}
//叶节点
class LeafNode : public VarBinNode{
private:
    Operand var;
public:
    LeafNode(const Operand& val){ var = val; }
    bool isLeaf(){ return true; }
    Operand value(){ return var; }
}
//内部节点（分支节点）
class IntlNode : public VarBinNode{
private:
    VarBinNode* left;
    VarBinNode* right;
    Operator opx;
public:
    IntlNode(const Operator& op, VarBinNode* l, VarBinNode* r){
        opx = op;
        left = l;
        right = r;
    }
    bool isLeaf(){ return false; }
    VarBinNode* leftchild(){ return left; }
    VarBinNode* rightchild() { return right; }
    Operator value(){ return opx; }
}
//前序遍历
void traverse(VarBinNode* subroot){
    if(subroot == NULL) return;
    if(subroot->isLeaf())
        cout << "Leaf:"
             << ((LeafNode*)subroot)->value() << endl;
    else{
        cout << "Internal："
             << ((IntlNode*)subroot)->value() << endl;
        traverse(((IntlNode*)subroot)->leftchild());
        traverse(((IntlNode*)subroot)->rightchild());
    }
}

结构性开销

存储左右节点的指针占据空间（结构性开销）。
内部节点可能不存储数据，空间使用率低。

降低结构性开销：数组实现完全二叉树

完全二叉树的特性，节点的填充是有顺序的，从左到右。如果按顺序塞入数组元素，则根据数据下标即可知道父节点、左/右子节点。
设节点总数n，范围（0 ~ n - 1），节点 r 的亲属计算公式如下：

Parent(r) = (r - 1) / 2;    //当 r != 0 时。
Leftchild(r)= 2r + 1;         //当 2r + 1 < n 时。
Rightchild(r) = 2r + 2;        //当 2r + 2 < n 时。
Leftsibling(r) = r - 1;        //左兄弟，r为偶数且0 <= r <= n-1时
Rightsibling(r) = r + 1;    //右兄弟，r为奇数且r + 1 < n时

3、二叉查找树

Binary Search Tree，BST，二叉检索树，二叉排序树。
无序表实现的字典，插入很快（末端），查找O(n)。
数组有序表实现的字典，二分查询O(n)，插入很慢。

二叉查找树，满足条件：左子树值 <= 根值 <= 右子树值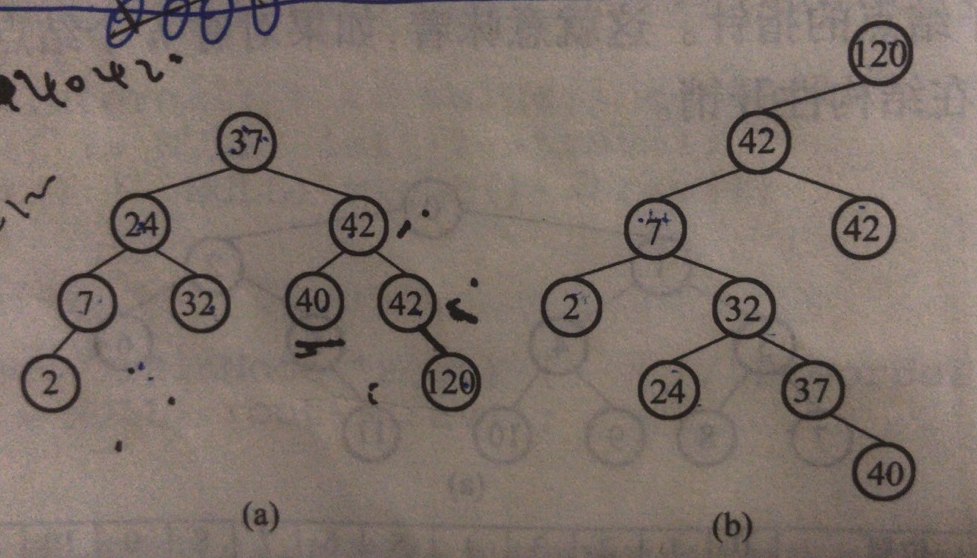

template<class Key,class Elem, class KEComp, class EEComp>
class BST : public Dictionary<Key, Elem, KEComp, EEComp>{
private:
    BinNode<Elem>* root;
    int nodecount;
private:
    void clearhelp(BinNode<Elem>*);        //删除全部节点
    //在节点r下插入一个值 = t的节点。返回被插入节点的父节点。
    //在二叉树中插入节点
    //r：    被插树的root节点
    //t：    插入节点的节点值
    //ret：    被插入节点的父节点
    BinNode<Elem>* inserthelp(BinNode<Elem>* r, const Elem& t);
    //删除r节点下的最小节点，保存在t，返回被删除节点的右子树。
    //删除二叉树的最小节点
    //r：    二叉树根节点
    //t：    被删除节点
    //ret：    被删除节点的右子树
    //注意“删除”，只是将值抹除。例如：
    //删除一个有left/right节点的节点target，其实就是：
    //target->setValue(right子树中的最小值)
    BinNode<Elem>* deletemin(BinNode<Elem>* r, BinNode<Elem> *& t);    
    //删除r节点下满足K的子节点，并保存在t。返回
    //删除二叉树中指定Key的节点
    //r：    二叉树根节点
    //K：    指定Key值
    //t：    被删除节点
    //ret：    二叉树不存在Key的节点，返回r，注意递归调用每个r不同
    //   ：    存在Key的节点，返回值有三种情况：
    //   ：    如果被删节点只有一个子节点，则返回子节点
    //   ：    如果被删节点有两个子节点，就返回被删节点指针，从有节点中选择最小节点的值赋值给被删节点。
    BinNode<Elem>* removehelp(BinNode<Elem>* r, const Key& Key, BinNode<Elem> *& t);
    //查找r节点下满足K的子节点，并保存在t
    bool findhelp(BinNode<Elem>* r, const Key& K, Elem& t) const;
    //中序遍历
    void printhelp(BinNode<Elem>*, int) const;
public:
    BST(){
        root = NULL;
        nodecount = 0;
    }
    ~BST(){
        clearhelp(root);
    }
    void clearhelp(BinNode<Elem>* subroot){
        if(subroot == NULL) return;
        clearhelp(subroot->left());
        clearhelp(subroot->right());
        delete subroot;
    }
    BinNode<Elem>* inserthelp(BinNode<Elem>* subroot,const Elem& e){
        if(subroot == NULL) return NULL;
    }
    //一直沿着左子树找，直到没有左子树。
    BinNode<Elem>* deletemin(BinNode<Elem>* subroot, BinNode<Elem>* &min){
        if(subroot->left() == NULL){    //没有左子树，说明subroot就是最小节点
            min = subroot;    //最小节点
            return subroot->right();    //返回最小节点的右子树，方便递归的时候，
                                        //把这个右子树设置成被删节点父节点的左子树。
                                           //也就是代替被删节点。
        }
        else{    
            //这个setleft有两种情况：
            //
            //第一种情况：递归到了最左节点，也就是
            //deletemin返回被删节点右子树
            //此时的subroot是被删节点的父节点
            //所以setleft是把subroot的左子树设置为被删节点的右子树。
            //
            //第二种情况：递归途中，返回的就是递归节点
            //此时的subroot就是递归节点，deletemin返回的就是subrrot的左子节点
            //所以setleft其实没干什么，但是这样代码更简化，唯一作用就是上面的第一种情况。
            subroot->setLeft(deletemin(subroot->left(), min));
            //递归过程中，还没递归到最左节点，则返回递归节点
            return subroot;
        }
    }
    BinNode<Elem>* removehelp(BinNode<Elem>* subroot, const Key& K, BinNode<Elem>*& t){
        if(subroot == NULL) return NULL;
        else if(KEComp::lt(K, subroot->val()))
            subroot->setLeft(removehelp(subroot->left(), K, t));
        else if(KEComp::gt(K, subroot->val()))
            subroot->setRight(removehelp(subroot->right(), K, t));
        else{
            BinNode<Elem>* temp;
            t = subroot;
            if(subroot->left() == NULL)
                subroot = subroot->right();
            else if(subroot->right() == NULL)
                subroot = subroot->left();
            else{
                subroot->setRight(deletemin(subroot->right(), temp));
                Elem te = subroot->val();
                subroot->setVal(temp->val());
                temp->setVal(te);
                t = temp;
            }
        }
        return subroot;
    }
    bool findhelp(BinNode<Elem>* subroot, const Key& K, Elem& e){
        if(subroot == NULL) return false;
        else if(KEComp::lt(K, e)) return findhelp(subroot->leftchild(), K, e);
        else if(KEComp::gt(K, e)) return findhelp(subroot->rightchild(), K, e);
        else{
            e = subroot->val()；
            return true;
        };
    }
    //中序遍历
    void printhelp(BinNode<Elem>* subroot, int level){
        if(subroot == NULL) return;
        printhelp(subroot->left(), level + 1);
        for(int i = 0; i < level; i++){
            cout << " ";
        }
        cout << subroot->val() << "\n";
        printhelp(subroot->right(), level + 1);
    }
//以下是字典的虚函数
public:  
    void clear(){    //重新初始化
        clearhelp(root);
        root = NULL;
        nodecount = 0;
    }
    bool insert(const Elem& e){            //插入一个元素
        root = inserthelp(root, e);
        nodecount++;
        return true;
    }
    bool remove(const Key& K, Elem& e){        //根据key删除元素
        BinNode<Elem>* t = NULL;
        root = removehelp(root, K, t);
        if(t == NULL) return false;
        e = t->val();
        nodecount++;
        delete t;
        return true;
    }
    //按照自定义规则删除一个元素，循环执行则最终会清空字典。
    bool removeAny(Elem& e){
        if(root = NULL) return false;
        BinNode<Elem>* t;
        root = deletemin(root, t);
        e = t->val();
        delete t;
        nodecount++;
        return true;
    }        
    bool find(const Key&, Elem&){        //根据key查找元素
        return findhelp(root, K, e);
    }    
    int size(){
        return nodecount;
    }
    void print(){
        if(root == NULL) cout << "the BST is empty.\n";
        else printhelp(root, 0);
    }
}

查插删改性能

1、findhelp、inserthelp取决于深度depth。
2、removehelp取决于被删节点的depth。
3、遍历复杂度 = O(n)。
4、log n <= 树深度depth <= n，depth越小，树越平衡。
5、算法最差O(n)，最好O(log n)。
6、二叉查找树平衡度不稳定，所以性能也不稳定。

4、堆与优先队列

堆是完全二叉树，根、左、右存在相同的关系R。
完全二叉树使得平衡度最大化。

根节点：parent，左右节点：left、child。
最大值堆：parent >= max(left，right)的完全二叉树，max-heap。root最大。
最小值堆：parent <= min(left，right)的完全二叉树，min-heap。root最小。
注意和二叉查找树区分：

template<class Elem, class Comp>
class maxheap{
private:
    Elem* Heap;        //堆的物理结构，数组，节点位置pos就是相应的数组下标。
                    //所以0是堆顶，完全二叉树特性，n/2以后是叶节点。
                    //建堆的情况有两种：
                    //一：构造函数的时候，传入了一个数组的数据，然后这些数据进行建堆。
                    //二、构造的时候是空的，然后一个一个insert进来。
    int size;        //堆的空间大小
    int n;            //当前元素个数
    void siftdown(int pos);        //pos的左右子树已经是堆。
                                //把pos节点“下沉”到正确的位置，即父节点比左右子节点大。
public:
    maxheap(Elem* h, int num, int max);    //数组h有num个元素，数组总长度是max。
    int heapsize() const ;            //堆空间大小
    bool isLeaf(int pos) const;        //pos是否是叶节点位置
    int leftchild(int pos) const;    //pos是左节点？
    int rightchild(int pos) const;    //pos是右节点？
    int parent(int pos) const;        //pos的父节点位置
    bool insert(const Elem&);        //插入元素，注意插入过程可不像BST
                                    //为了保持完全二叉树结构，首先插入堆最后面
                                    //然后“上浮”到正确位置（不断与父节点比较）
    bool removemax(Elem&);            //删除根节点，注意实际上没有真的delete。
                                    //根节点和最后一个节点交换，然后新的根节点“下沉”
                                    //到正确位置，此时的最后一个节点就是删除的根节点。
                                    //在堆排序，用的上，removemax的过程其实就是排序的过程
    bool remove(int pos, Elem&);    //删除pos位置节点
                                    //pos位置节点和最后一个节点n对换
                                    //接下来同removemax工作。
    void buildheap();                //Heapify contents of Heap，一个一个插入元素
private:
    void siftdown(int pos){
        while(!isLeaf(pos)){
            int maxChildPos = leftchild(pos);
            int rc = rightchild(pos);
            if((rc < n) && Comp::lt(Heap[maxChildPos], Heap[rc]))
                maxChildPos = rc;
            if(!Comp::lt(Heap[pos], Heap[maxChildPos])) return;
            swap(Heap, pos, maxChildPos);
            pos = maxChildPos;
        }
    }
public:
    maxheap(Elem* h, int num, int max){
        Heap = h;
        n = num;
        size = max;
        buildHeap();
    }
    int heapsize() const{ return n; }
    bool isLeaf(int pos) const { return (pos >= n / 2) && (pos < n); }
    int leftchild(int pos) const{ return pos*2 + 1; }
    int rightchild(int pos) const{ return pos*2 + 2; }
    int parent(int pos) const{ return (pos-1) / 2; }
    bool insert(const Elem& val){
        if(n >= size) return false;
        int curr = n++;
        Heap[curr] = val;    //为了保持完全二叉树结构，插入堆尾，也就是数据最后一位。
        while((cur != 0) && (Comp::gt(Heap[curr], Heap[parent(curr)]))){
            //将堆尾节点“上浮”到正确位置。
            swap(Heap, curr, parent(curr));
            curr = parent(curr);
        }
        return true;
    }
    bool removemax(Elem& it){
        if(n == 0) return false;
        swap(Heap, 0, --n);        // 把最后一个节点和根节点对调
        if(n != 0) siftdown(0);    // 把新的root节点重新“下沉”
        it = Heap[n];    // swap之后，n位置的节点就是要删除的root节点
        return true;
    }
    bool remove(int pos, Elem& t){
        if((pos< 0) || (pos >= n)) return false;
        swap(Heap, pos, --n);
        //这是教材中的一段代码，不为什么考虑pos节点和父节点的比值，
        //按理说父节点肯定是大于pos节点值的。此时pos值为堆尾节点
        //按理说肯定是更大的，无需考虑交换的，没有明白？？？？
        while((pos != 0) && (Comp::gt(Heap[pos], Heap[parent(pos)])))
            swap(Heap, pos, parent(pos));
        siftdown(pos);    //将新插入的堆尾节点“下沉”到正确位置。
        it = Heap[n];
        return true;
    }
    void buildheap(){
        //n / 2之后是叶节点，无需移动
        for(int i = n / 2 - 1; i >= 0; i--)
            siftdown(i);
    }
}

5、Huffman编码树

5.1、构建Huffman树

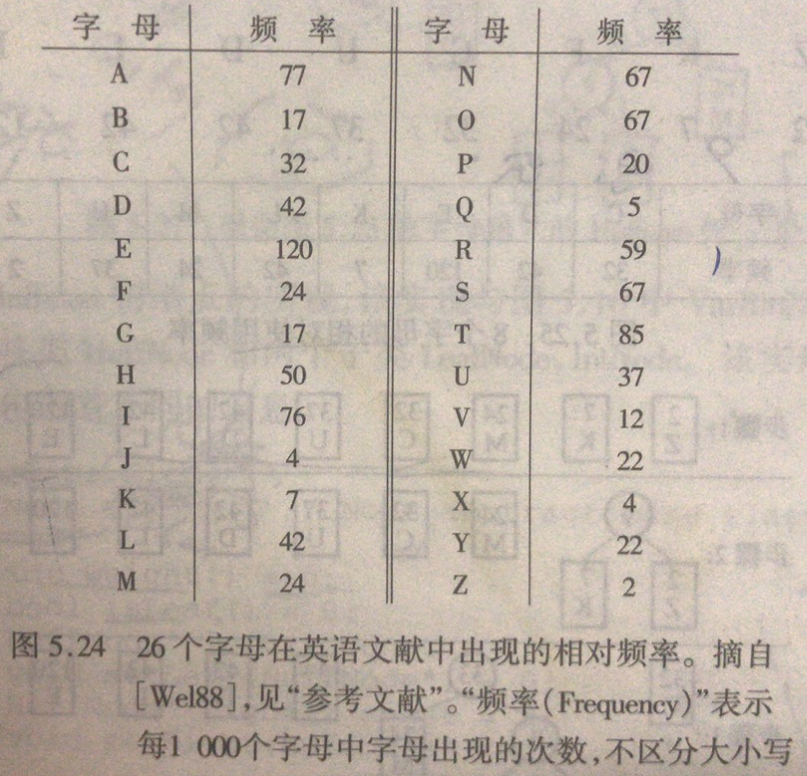
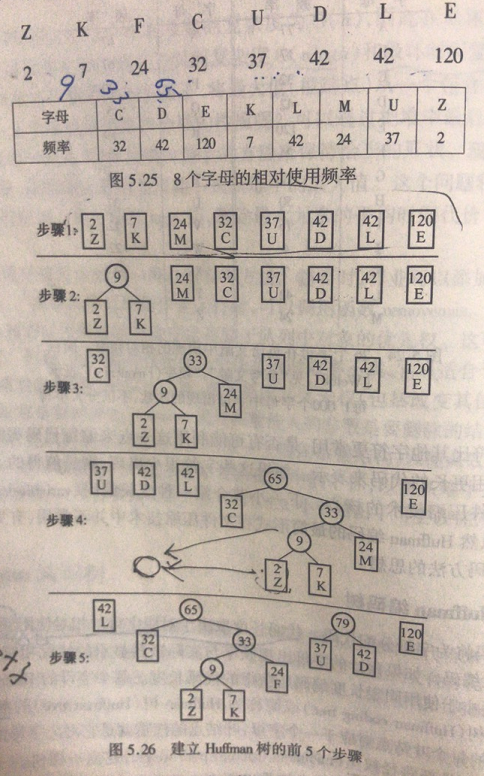
类设计：
HuffNode：哈弗曼树的节点基类（内部节点、叶节点）。
LeafNode：叶节点，存储权重和字母值。
IntlNode：内部节点，存储子节点权重和。
FreqPair：字母-频率数的数据对，叶节点保存值用。
HHComp：哈弗曼树的compare函数（比较根权重）
HuffTree：哈弗曼树的类

buildHuff：通过一个有序链表来对不断构建的HuffTree进行保存和排序。顺序是从HHComp的方法排列。

template<class Elem>
class HuffNode{
public:
    virtual int weight() = 0;
    virtual bool isLeaf() = 0;
    virtual HuffNode* left() const = 0;
    virtual HuffNode* right() const = 0;
    virtual void setLeft(HuffNode*) = 0;
    virtual void setRight(HuffNode*) = 0;
}
//Huffman树的叶节点，保存字幕
template<class Elem>
class LeafNode : public HuffNode<Elem>{
private:
    FreqPair<Elem>* it;        //存储字母Elem、和他出现次数（权重）对。
public:
    LeafNode(const Elem& val, int freq){
        it = new FreqPair<Elem>(val, freq);
    }
    int weight(){ return it->weight() }
    FreqPair<Elem>* val(){ return it; }
    bool isLeaf(){ return true; }
    virtual void setLeft(HuffNode*){}
    virtual void setRight(HuffNode*){}
    virtual HuffNode* left() const{ return NULL; }
    virtual HuffNode* right() const{ return NULL; }
}
//Huffman树的内部节点。
template<class Elem>
class IntlNode : public HuffNode<Elem>{
private:
    HuffNode<Elem>* lc;
    HuffNode<Elem>* rc;
    int wgt;
public:
    IntlNode(HuffNode<Elem>* l, HuffNode<Elem>* r){
        wgt = l->weight() + r->weight();
        lc = l; rc = r;
    }
    int weight() { return wgt; }
    bool isLeaf(){ return false; }
    HuffNode<Elem>* left() const { return lc; }
    HuffNode<Elem>* right() const { return rc; }
    void setLeft(HuffNode<Elem>* b) { lc = (HuffNode*)b; }
    void setRight(HuffNode<Elem>* b) { rc = (HuffNode*)b; }
}
template<class Elem>
class FreqPair{
private:
    Elem it;
    int freq;
public:
    FreqPair(const Elem& e, int f){ it = e; freq = f; }
    ~FreqPair(){}
    int weight(){ return freq; }
    Elem& val() { return it; }
}
template<class Elem>
class HuffTree{
private:
    HuffNode<Elem>* theRoot;
public:
    HuffTree(Elem& val, int freq){
        theRoot = new LeafNode<Elem>(val, freq);
    }
    HuffTree(HuffTree<Elem>* l, HuffTree<Elem>* r){
        theRoot = new IntlNode<Elem>(l->root(), r->root());
    }
    ~HuffTree(){};
    HuffNode<Elem>* root(){ return theRoot; }
    int weight(){ return theRoot->weight(); }
}
template<class Elem>
class HHComp{
public:
    static bool lt(HuffTree<Elem>* x, HuffTree<Elem>* y){
        return x->weight() < y->weight();
    }
    static bool eq(HuffTree<Elem>* x, HuffTree<Elem>* y){
        return x->weight() == y->weight();
    }
    static bool gt(HuffTree<Elem>* x, HuffTree<Elem>* y){
        return x->weight() > y->weight();
    }
}
template<class Elem>
HuffTree<Elem>* buildHuff(SLList<HuffTree<Elem>*, HHCompare<Elem> >* fl){
    HuffTree<Elem> *temp1, *temp2, *temp3;
    for(fl->setStart(); fl->leftLength() + fl->rightLength() > 1; fl->setStart()){St
        //第二个setStart是因为循环中remove链表节点
        //需要setStart重新定位栅栏到头部。
        fl->remove(temp1);
        fl->remove(temp2);
        temp3 = new HuffTree<Elem>(temp1, temp2);
        fl->insert(temp3);
        delete temp1;
        delete temp2;
    }
    return temp3;
}

5.2、Huffman编码

点击查看【processon】

二、一般树（general tree）

前序、后序遍历和二叉树差不对，中序遍历一般用不到，因为子节点数量不确定。

1、ADT（右兄弟表示法）

一个（最左节点），以及下一个（右邻近）兄弟节点。即可遍历全部节点。

template<class Elem>
class GTNode{
public:
    GTNode(const Elem&);
    ~GTNode();
    Elem value();
    bool isLeaf();
    GTNode* parent();
    GTNode* leftmost_child();    //最左子节点
    GTNode* right_sibling();    //右邻近 兄弟节点
    void setValue(Elem&);
    void insert_first(GTNode<Elem>*);        //插入到最左边子节点左边
    void insert_next(GTNode<Elem>*);        //插入到最右边节点右边
    void remove_first();    //同上
    void remove_next();        //同上
}
template<class Elem>
class GenTree{
private:
    void printHelp(GTNode*);    //打印树
public:
    GenTree();
    ~GenTree();
    void clear();
    GTNode* root();
    void newroot(Elem&, GTNode<Elem>*, GTNode<Elem>*);
    void print();
private:
    // 前序遍历
    void printHelp(GTNode* subroot){
        if(subroot->isLeaf()) cout << "Leaf: ";
        else cout << "Internal: ";
        cout << subroot->value() << "\n";
        for(GTNode<Elem>* temp = subroot->leftmost_child(); temp != NULL;
            temp = temp->right_sibling())
            printhelp(temp);
    }
}

2、ADT（父指针表示法）

每个节点只保存父节点指针，虽然没有右兄弟法存储的信息多，但是足够解决一些有用问题。比如：
1、节点是否在同一树中（FIND，找（最）父节点）
2、归并两个集合（UNION）
称为UNION/FIND算法。

//array[k] = v，v是k的父节点
class GENtree{
private:
    int* array;
    int size;
    int FIND(int curr) const;
public:
    Gentree(int sz);
    ~Gentree();
    void UNION(int a, int b);    //并入a、b节点，使用他们有相同的最顶级根节点。
    bool differ(int a, int b);    //a、b是否有相同的最顶级根节点
}
private:
    int FIND(int curr) const{    //找到最顶层的根节点
        while(array[curr] != ROOT) curr = array[curr];
        return curr;
    }
    //路径压缩合并
    int FIND(int curr) const{
        if(array[curr] == ROOT) return curr;
        return array[curr] = FIND(array[curr]);
    }
public:
    Gentree(int sz){
        size = sz;
        array = new int[sz];
        for(int i = 0;i < sz;i++)
            array[i] = ROOT;
    }
    ~Gentree(){ delete[] array };
    //这里直接让b节点存储a节点的位置
    void UNION(int a, int b){    //这里直接让b节点存储a节点的位置
        int root1 = FIND(a);
        int root2 = FIND(b);
        if(root2 != root1) array[root2] = root1;
    }
    bool differ(int a, int b){ return FIND(a) == FIND(b); }
}

这个UNION涉及到如何合并，当然要使树的深度尽可能低，有两种方法：

重量权衡合并

在UNION的时候，“小”树合并到“大”树上，大小说的是树的深度。

路径压缩

每次FIND的时候，递归FIND，让一个节点指向ROOT，其他节点指向这个节点。

3、树的实现

方法一、节点数组，子节点链表

数组保存树的节点，每个节点保存：
一个子节点链表
一个父节点。
这样的话，难找兄弟节点。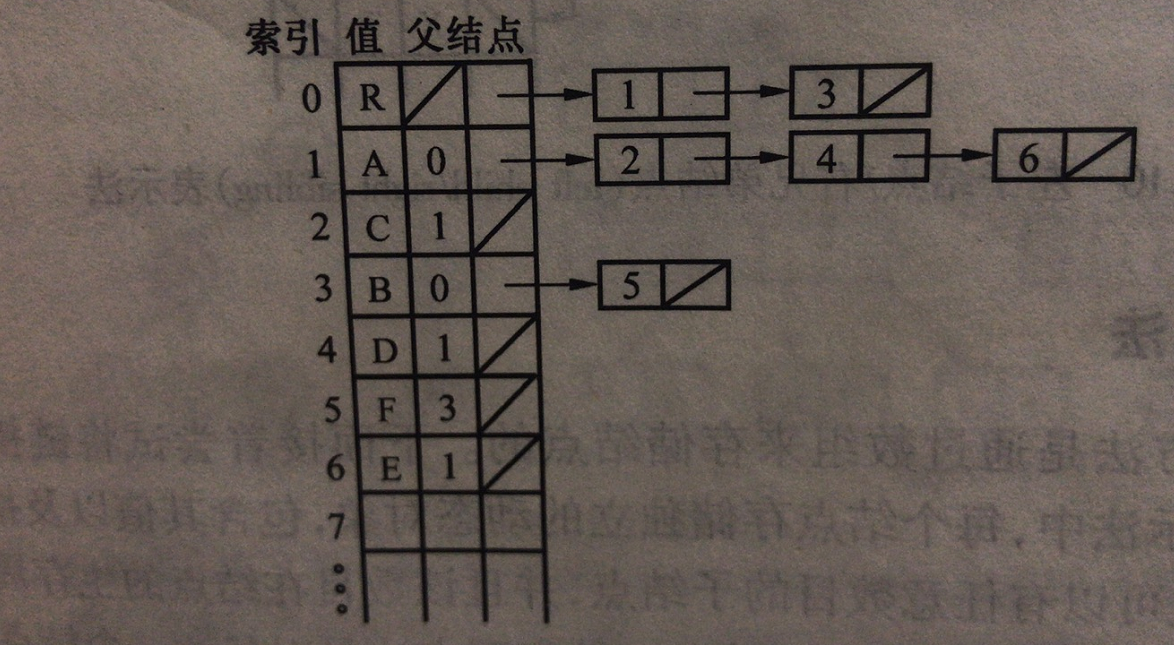

方法二：左子节点、右兄弟节点

数组保存树节点。
每个节点保存：
父节点、
最左子节点
右侧兄弟节点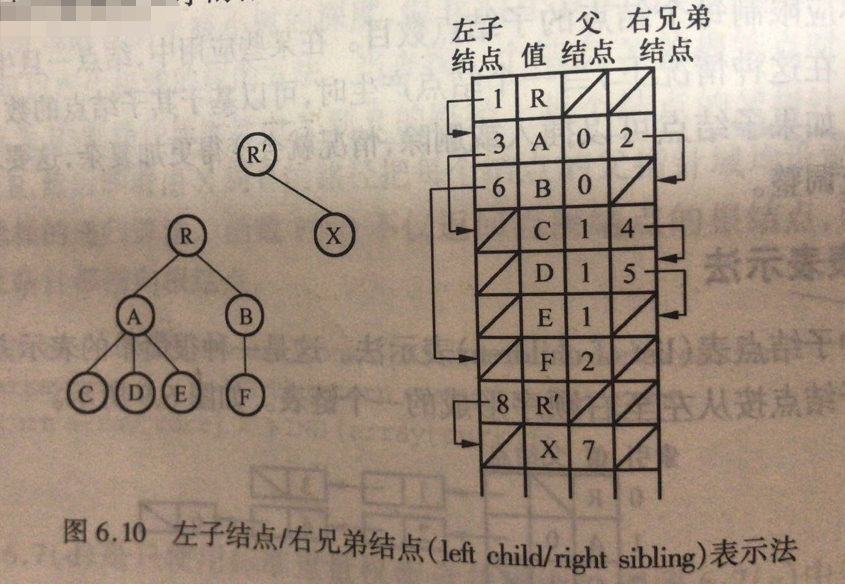

改进2：“动态子节点数组”表示法

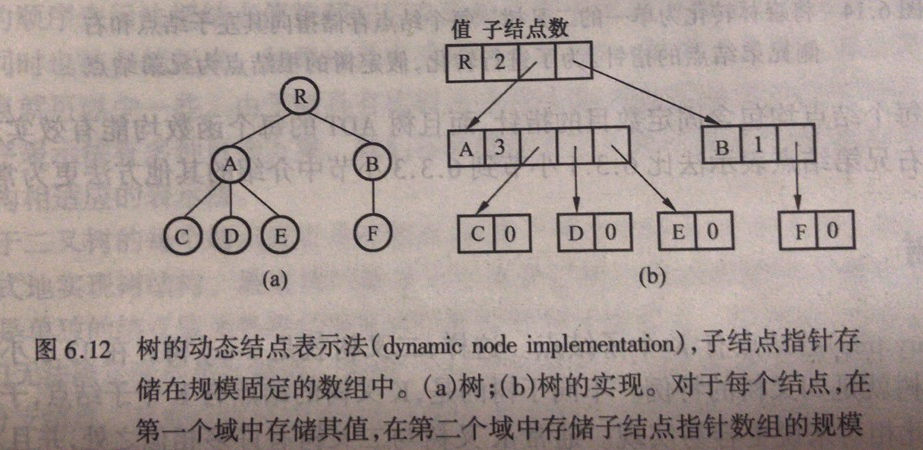
每个节点保存一个数组指针，数组存储的是子节点指针。在子节点创建的时候就知道了所有的子节点，创建的数组由可利用空间管理，当节点插入子节点时，数组又刚好满了，就从可利用空间要一个更大一点的数组，原来的数组回收。

方法3：“动态节点”表示法

树的节点由链表存储，每个节点又保存一个子节点链表。

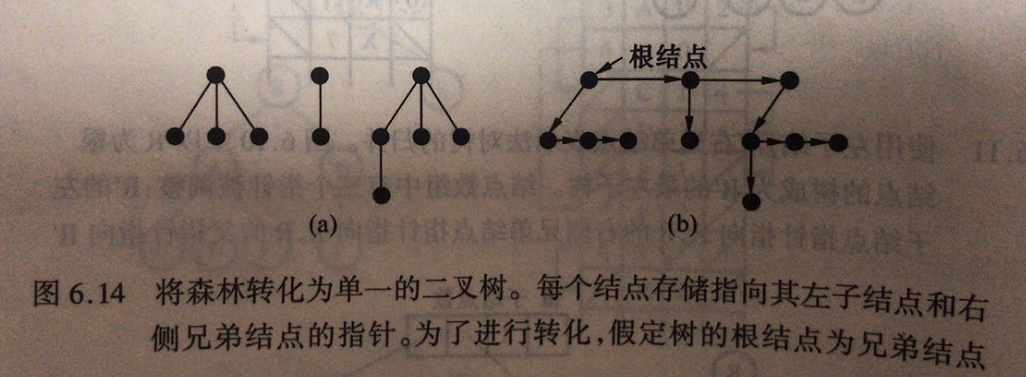
方法4：“化森林为二叉”

4、K叉树

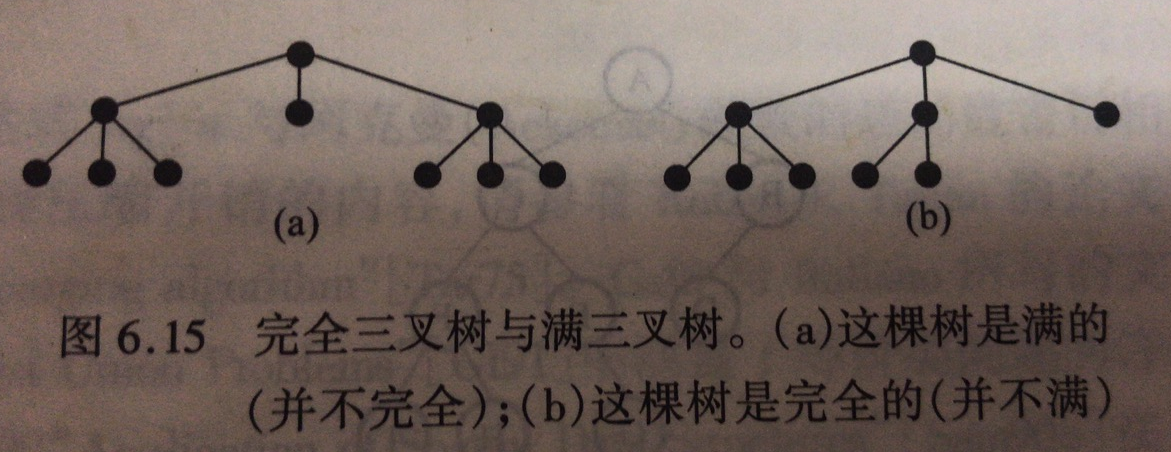
每个节点都固定有K个子节点。K = 2时，就是二叉树。

5、顺序树表示法

按前序遍历把节点顺序存储起来，这样节省空间，但访问耗时。