一、表示法

图元有多种表示方法，在不同情况下应该采用不同的方法。

1、隐式表示

定义一个布尔函数，如果点在图元上，则布尔值为真；否则为假。

2、参数形式

表示一个圆心在原点的单位圆。

只使用了一个参数，这些函数是单变量的。

单变量函数的轨迹是一条曲线，双变量函数的轨迹是一个曲面。

3、直接形式

用两个端点表示一条线段。
用球心、半径表示一个球。

4、自由度

无歧义地描述该实体所需信息量的最小数目。
同一几何图元的不同表示方法的自由度可能不同，这是由于图元参数化的冗余造成的 。这些冗余可以通过一些假设消除，如假设向量为单位长度。

二、直线、射线

• 经典几何中的定义
  • 直线向两个方向无限延伸
  • 线段是直线的有限部分，有两个端点。
  • 射线是直线的“一半”，有一个起点并向一个方向无线延伸
• 计算机科学和计算几何中
  • 射线是有向线段。有起点、终点。定义了位置、长度和方向。射线在计算几何和图形学中非常重要。

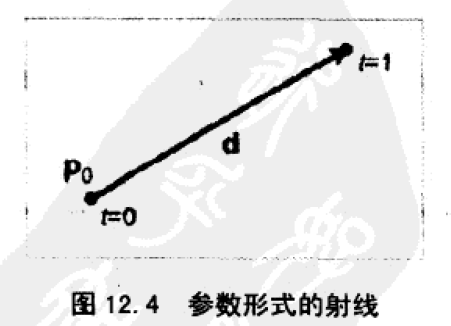
1、射线

射线两点表示方法：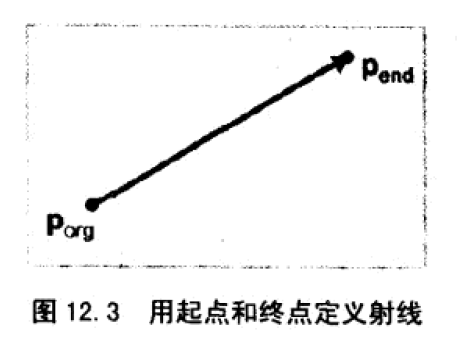

2D射线的参数形式：

3D射线的参数形式：

射线的向量形式表示

2、2D直线

2D直线隐式表示：

2D直线向量表示：，由上面形式改变。

2D直线斜截式表示：

• 斜率
  • m值，若，则表示每向上移动rise个单位，就会向右移动run个单位。
  • m=0，直线垂直于x轴。
• 截距
  • b值，直线和y轴相较于。

2D直线表示
1、垂直于直线的单位向量
2、给出原点到直线的距离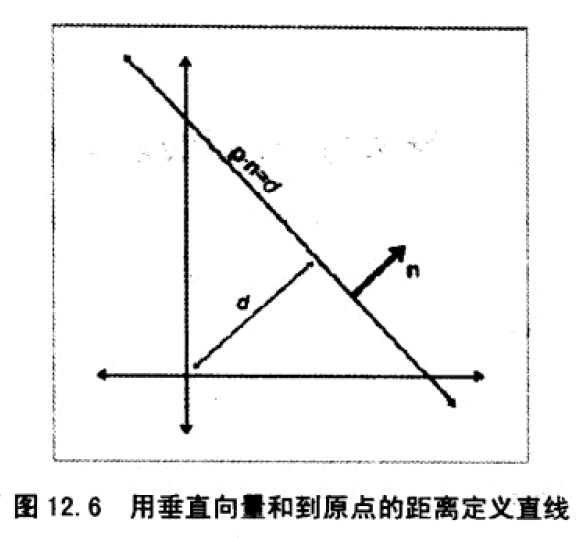

2D直线表示
垂直于直线的单位向量
直线上的一点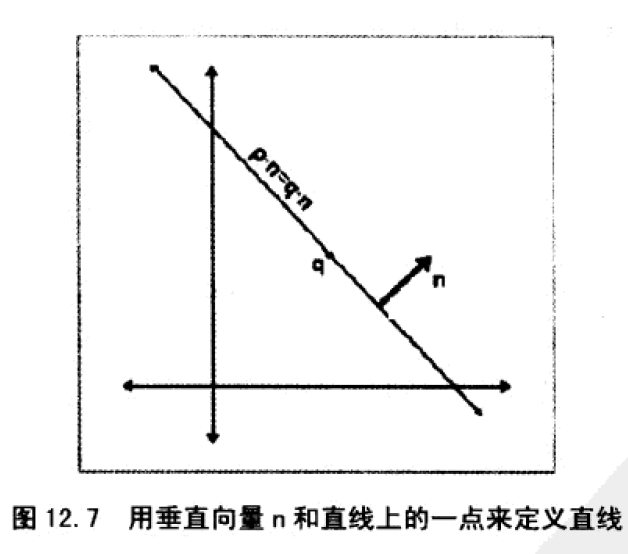

2D直线表示
垂直平分线来表示，直线的最初定义。
直线是到两个给顶点的距离相等的点的集合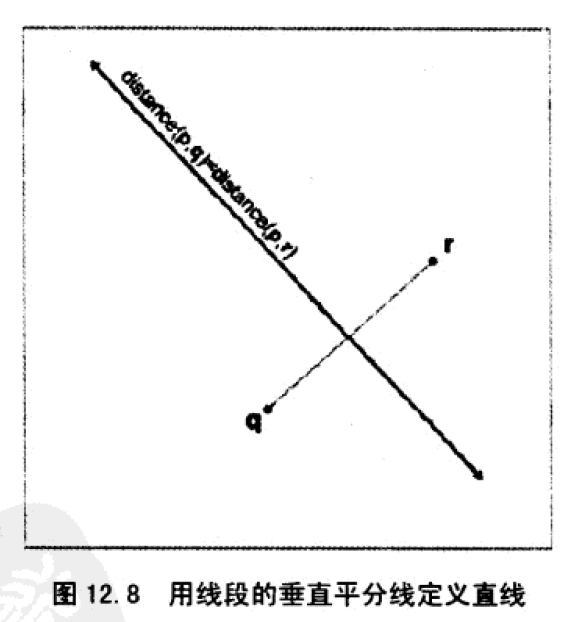

三、球和圆

1、球

常用于做物体界定。

球的定义：是点的集合，这些点到给定点的距离相等。
半径：球面到球心的距离。
球的直接表示形式：球心 + 半径

球的表示形式：

球的表示形式：

球的面积：

球的体积：

2、圆

直径**
经过圆心的直线与圆有两个交点，这两个点之间的距离称为直径。

。

四、矩形边界框

常用来界定物体，边可以是与轴对齐的或是任意方向的。

轴对齐矩形边界框
axially aligned bouding box，AABB**
边必须垂直于坐标轴，不一定是立方体。
3D的AABB是一个六面体。每边都平行于一个坐标面。

方向矩形边界框
oriented bouding box，OBB
**

AABB内的点满足以下不等式：

特别重要的两个顶点：

中心点

“尺寸向量”

“半径向量”

class AABB{
public:
    Vector3 min;
    Vector3 max;
}
void AABB3::empty() { 
    const float kBigNumber = 1e37f;            // 最大的数，表示未初始化。
    min.x = min.y = min.z = kBigNumber; 
    max.x = max.y = max.z = -kBigNumber;
}
// 扩展AABB：为了包含新的点，min和max必须改变。
void AABB3::add(const Vector3 &p){
    if (p.x < min.x) min.x = p.x;
    if (p.x > max.x) max.x = p.x;
    if (p.y < min.x) min.y = p.y;
    if (p.y > max.x) max.y = p.y;
    if (p.z < min.x) min.z = p.z;
    if (p.z > max.x) max.z = p.z;
}

1、AABB与边界球

两者都用于界定物体，大多数情况下，AABB要更合适。

• 计算一个点集的AABB要简单的多
• 大多数情况下，AABB的体积要比球小得多。
  • 根本原因：球的自由度只有一个，AABB有三个。

只有星形图，AABB比边界球大，但是没大多少。
AABB对物体的方向敏感，看枪的图。

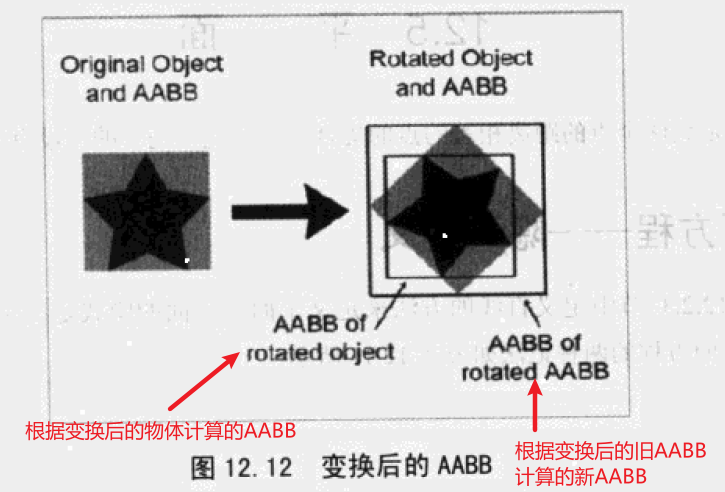
2、AABB的变换

物体发生变换，AABB也要重新计算。

• 方法一：根据变换后的物体坐标计算新的AABB，
  • 计算代价大，顶点太多，
  • AABB的体积不会过大造成浪费。
• 方法二：旧的AABB八个顶点跟着变换后，根据这个8个顶点计算新的AABB，
  • 计算代价小，
  • 可能导致AABB的体积明显增大。

五、平面

在3D中，到两个指定点的距离相等的点的集合。

1、平面定义1

2、平面定义2

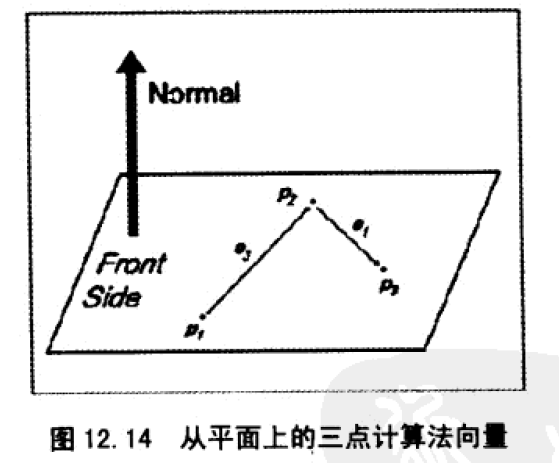
三个不共线的点唯一确定一个平面。
如下图，按左手坐标系规则，以逆时针列出三个不共线顶点，得到两个边：

3、平面定义3

三个顶点确定平面的缺点**

• 三个点可能共线
• 数值精度问题（三个点接近共线）
• 三个顺序问题导致求法向量错误（多边形上的三个点，这个三个顶点刚好在凹陷处）

根据平面上多个顶点，求法向量公式如下：

计算点集中最佳法向量，C++代码如下：

// 计算点集中最佳法向量，这些点都在同一个平面上。
Vector3 computeBestFitNormal (const Vector3 v[], int n) {
    Vector3 result = kZeroVector;
    const Vector3 *p = &v[n-1];                        // 从最后一个顶点开始,避免在循环中做if判断
    for (int i = 0; i < n; ++i) {                    // 迭代所有顶点
        const Vector3 *c =&v[i];                    // 得到“当前”顶点
        result.x += (p->z + c->z) * (p->y - c->y);    // 边向量乘积相加
        result.y += (p->x + c->x) * (p->z - c->z);
        result.z += (p->y + c->y) * (p->x - c->x);
        p = c;                                        //下一个顶点
    }
    result.normalize();        // 正则化结果并返回
    return result:
}

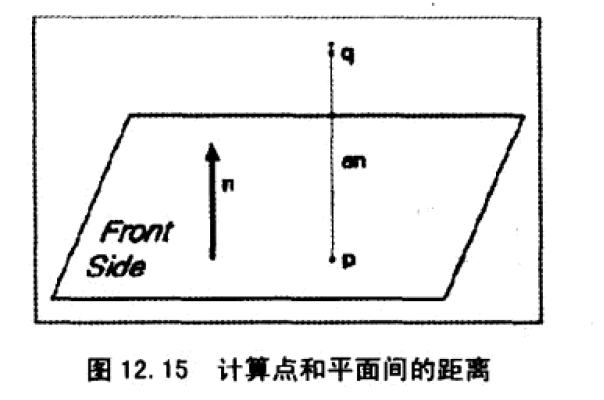
4、任意点到平面的距离

六、三角形

三角形在建模和图形学中极其重要，复杂的3D物体表面都是用三角形模拟的。像这样一组相连的三角形称作三角网格。

1、基本性质

在左手坐标系中，当从三角形“正面”看时，经常以顺时针方向列出这些点。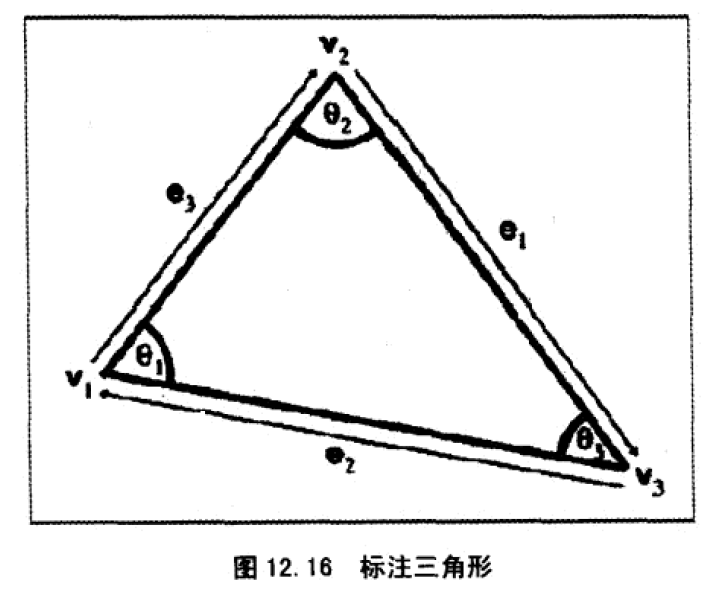

三角形正弦公式

三角形余弦公式

2、求面积

海伦公式

顶点坐标

叉乘

两向量叉乘的大小等于以该向量为边的平行四边形的面积。

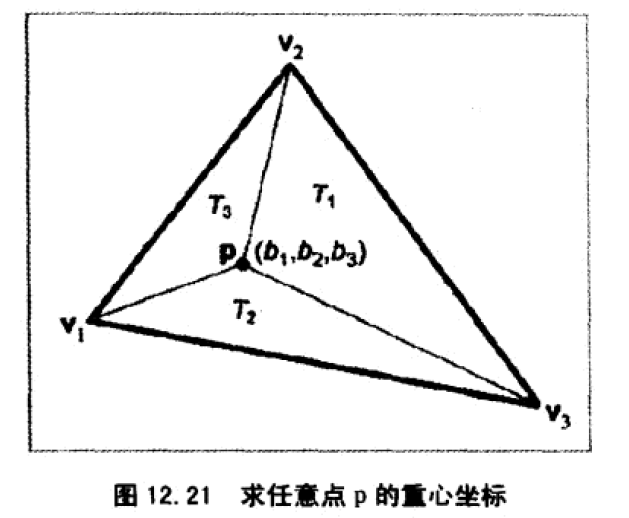
3、重心坐标空间

• 需求
  • 3D物体由于三角形组成，但三角形是一个平面，在3D中任意朝向的三角形表面移动是一件麻烦事。
• 定义
  • 三角形所在平面的任意点都能表示为顶点的加权平均值，这个权称作重心坐标。

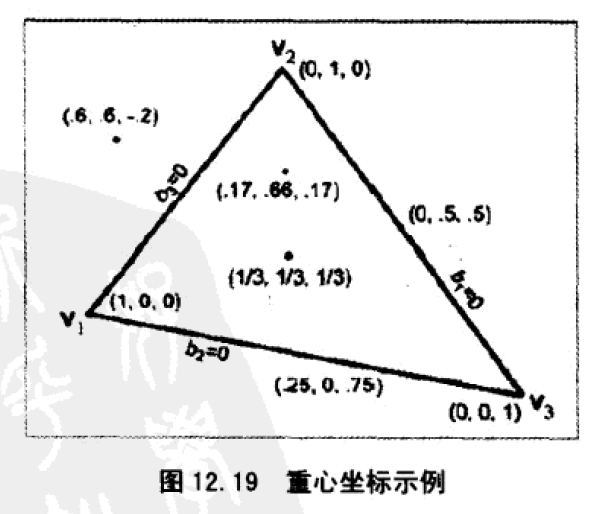
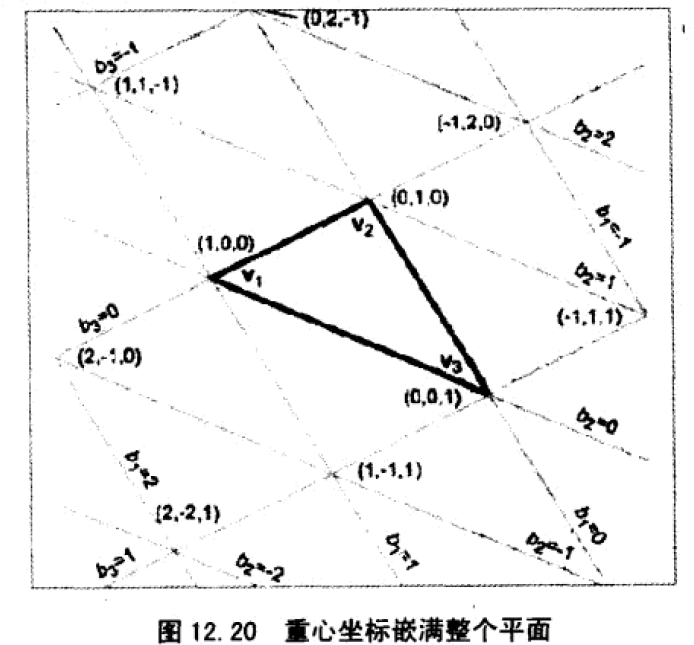
重心坐标本质上是2D的，不同于3D笛卡尔坐标，原因是重心坐标和=1，实际的自由度是2，是一个2D坐标系空间。

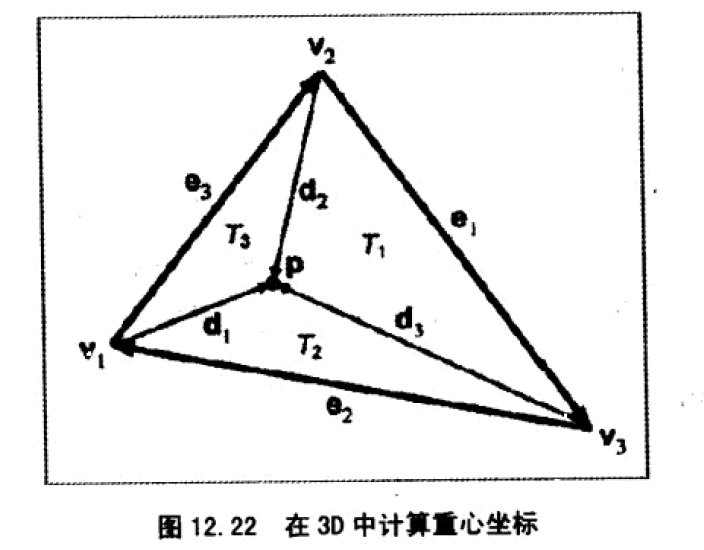
重心坐标计算_2D

重心坐标计算_3D

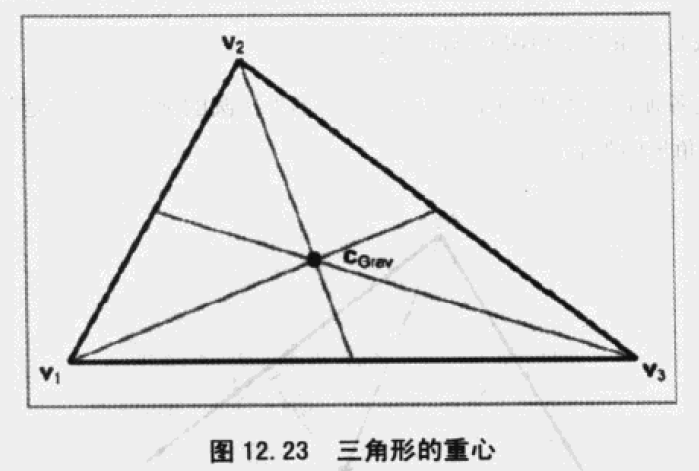
4、特殊点

重心

三角形最佳平衡点，中线的交点（顶点到对边中点的连线）。
重心是三个顶点的几何平均值：

重心坐标为，重心也被称作质心。

内心

内切圆的圆心，到三边距离相等的点。角平分线的交点。
解决了寻找与三条直线相切的圆的问题。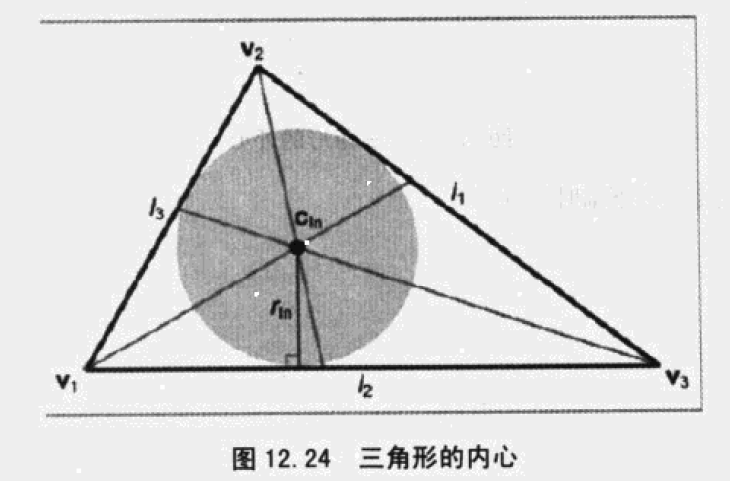

内心的重心坐标为：

内切圆的半径为：

外心

外接圆的圆心，到三顶点距离相等的点。垂直平分线的交点。
解决了寻找过三个点的圆的问题。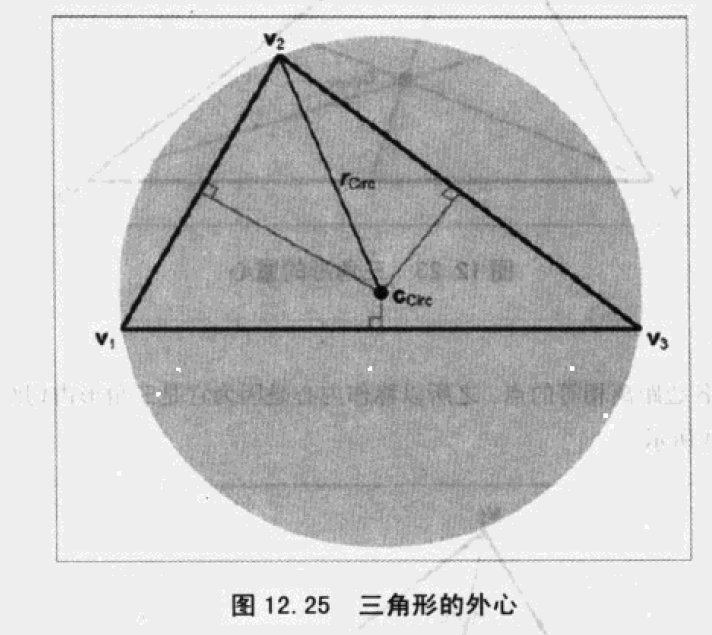


令：

外心坐标：

外心的重心坐标：

外接圆半径：

七、多边形

polygon，很难给多边形下一个简单的定义，不同场合精确定义不同。一般来说，多边形是由顶点和边构成的平面物体。

1、简单/复杂多边形

• 简单多边形
  • 不包含“洞”。
  • 可沿边列出所有顶点。
  • 使用频率很高。
• 复杂多边形
  • 可能包含“洞”

通过添加一对“接缝”边，将任意复杂多边形转化成简单多边形，接缝边的方向相反。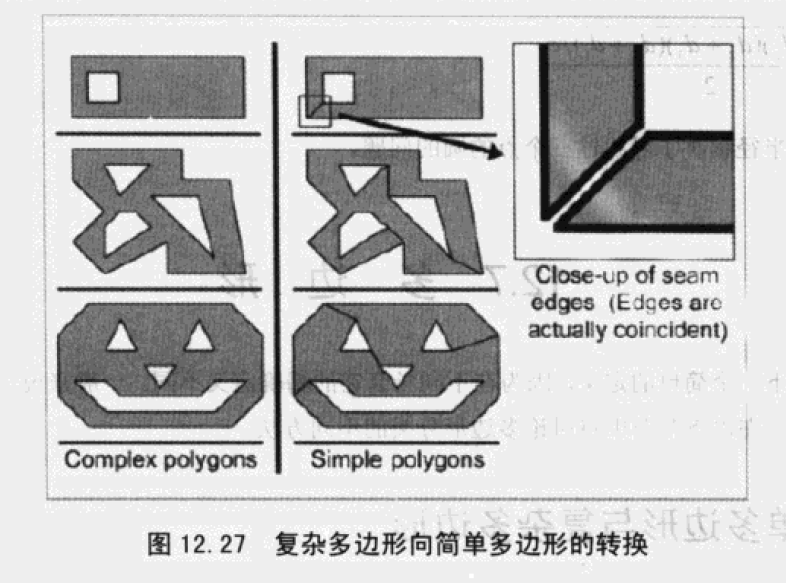

2、（非）自相交多边形

大多数简单多边形的边不相交，有的边相交了称为自相交多边形，一般与非自相交多边形打交道。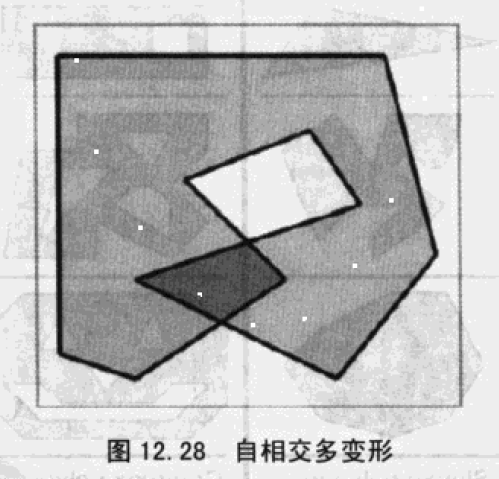

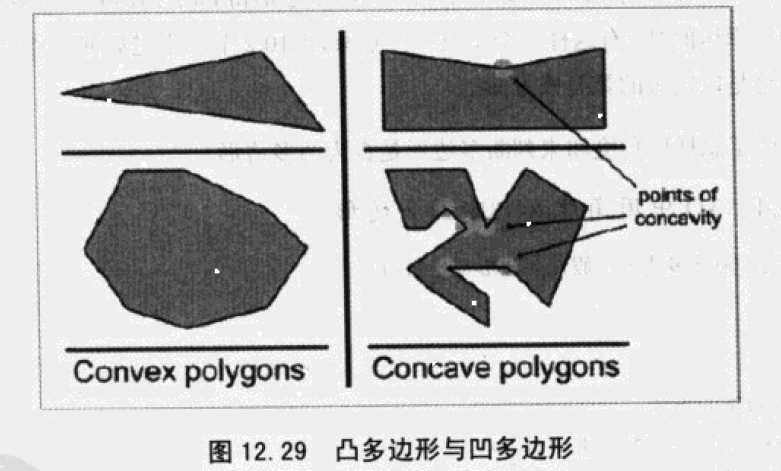
3、凸/凹多边形

• 直观上，有没有凹陷处
  • 凸多边形没有“凹陷处”，凹多边形至少有一个顶点在凹陷处（凹点）
• 顶点连线是否在内部
  • 凸多边形：任意两顶点的连线都包含在多边形中。
  • 凹多边形：总能找到一对顶点，连线有一部分在多边形外。
• 沿边，顶点方向是否一致
  • 凸多边形，沿边移动，每个顶点的转向都是相同。
  • 凹多边形：一些向左，一些向右，在凹点的转向是相反的（仅考虑非自交多边形）

分解凹多边形

如何把任意凹多边形分解为凸多边形片，基本思路是定位凹点（“反射顶点”）并通过添加对角线来有系统地移除它们。

凹/凸多边形检测

方法一：内角和
第一步，n个顶点的多边形，内角和为

• 证明方法一
  • 任意n顶点的凸多边形都能分解成n-2个三角形。
• 证明方法二
• 

第二步，凹多边形的内角和也是，但是凸多边形的内角都不会大于外角，凹多边形至少有一个内角大于对应的外角，因此多边形的每个顶点的内外角中较小者相加等于则该多边形是凸多边形。
通过两向量的点乘计算的夹角，返回的是以较短的弧度来度量的的，也就是更小的那个角。

// 判断多边形是否为凸多边形，假设多边形是平面的
//
// 输入：
// n:    顶点数目
// v1:    指向顶点数组的指针
//
// 输出：
// true:    是凸多边形
// false    是凹多边形
bool isConvex(const int n, const Vector3 v1[]) {
    float angleSum = 0.0f;                    // 内角和
    for (int i < 0; i < n; ++i) {            // 遍历整个多边形，将角度相加
        Vector3 e1 = i == 0 ? (v1[n - 1] - v1[i]) : (v1[i - 1] - v1[i]);
        Vector3 e2 = i == n - 1 ?(v1[0] - v1[i]) : (v1[i + 1] - v1[i]);
        e1.normalize();                     // 标准化并计算点乘
        e2.normalize(); 
        float theta = safeAcos(e1 * e2);    // 计算较小的角，用 “安全”反三角函数,避免发生数值精度问题
        angleSum += theta;
    }
    float convexAngleSum = (float)(n - 2) * kPi;            // 内角和=(n-2)*180°
    if (angleSum < convexAngleSum - (float)n * 0.OOO1f) (    // 判断凸凹性，允许一些经验数值误差
        return false;    // 凹多边形
    }
    return true;        // 凸多边形
}

方法二：检测“凹点”
没有凹点，是凸多边形，否则凹多边形。
基本思想就是每个顶点的转向应该一致，利用边相量叉乘检测，在左手坐标系中，如果向量的转向是顺时针，则它们的叉乘指向你。将相邻边向量的叉乘与法向量点乘，如果为负，则顶点是凹点。

4、三角形分解

任意多边形都能分解为三角形。所有的三角形操作都能应用到多边形上。

扇形分解

简单多边形的分解非常简单：选取一个点，沿着顶点按“扇形”分解多边形，得到个三角形。

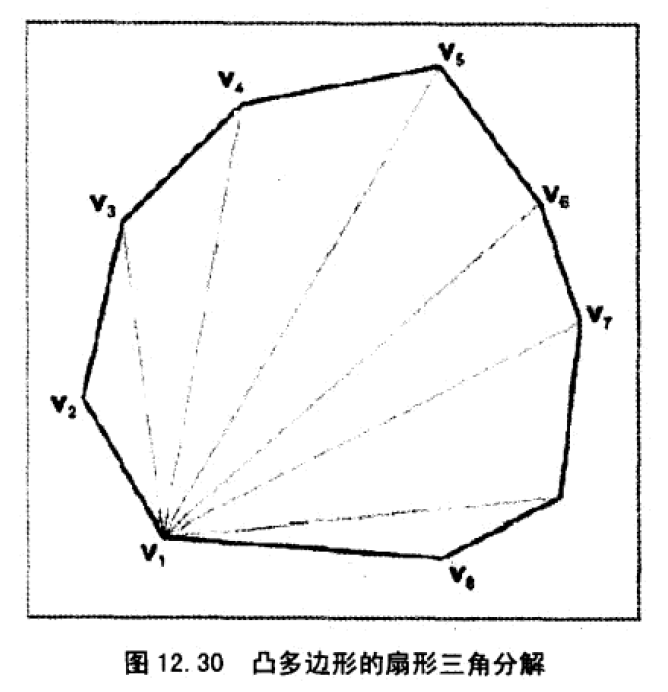
这种分解可能产生细长的三角形，可能会造成精度问题。一种更加聪明的方法是，不是沿着顶点按顺序分解，而是挑出这样一条两顶点对角线，使得顶点端点的两内角（总共4个）的最小者最大化，然后将多边形分成两部分，对该两部分递归执行上述方法。这种方法比较复杂，实践中，简单的扇形分解就足够简单了。