7.8 Adam算法

Adam算法在RMSProp算法基础上对小批量随机梯度也做了指数加权移动平均 [1]。下面我们来介绍这个算法。

所以Adam算法可以看做是RMSProp算法与动量法的结合。

7.8.1 算法

Adam算法使用了动量变量和RMSProp算法中小批量随机梯度按元素平方的指数加权移动平均变量，并在时间步0将它们中每个元素初始化为0。给定超参数（算法作者建议设为0.9），时间步的动量变量即小批量随机梯度的指数加权移动平均：

%20%5Cboldsymbol%7Bg%7Dt.%20%0A#card=math&code=%5Cboldsymbol%7Bv%7D_t%20%5Cleftarrow%20%5Cbeta_1%20%5Cboldsymbol%7Bv%7D%7Bt-1%7D%20%2B%20%281%20-%20%5Cbeta_1%29%20%5Cboldsymbol%7Bg%7D_t.%20%0A)

和RMSProp算法中一样，给定超参数（算法作者建议设为0.999），
将小批量随机梯度按元素平方后的项做指数加权移动平均得到：

%20%5Cboldsymbol%7Bg%7Dt%20%5Codot%20%5Cboldsymbol%7Bg%7D_t.%20%0A#card=math&code=%5Cboldsymbol%7Bs%7D_t%20%5Cleftarrow%20%5Cbeta_2%20%5Cboldsymbol%7Bs%7D%7Bt-1%7D%20%2B%20%281%20-%20%5Cbeta_2%29%20%5Cboldsymbol%7Bg%7D_t%20%5Codot%20%5Cboldsymbol%7Bg%7D_t.%20%0A)

由于我们将和中的元素都初始化为0，
在时间步我们得到%20%5Csum%7Bi%3D1%7D%5Et%20%5Cbeta_1%5E%7Bt-i%7D%20%5Cboldsymbol%7Bg%7D_i#card=math&code=%5Cboldsymbol%7Bv%7D_t%20%3D%20%20%281-%5Cbeta_1%29%20%5Csum%7Bi%3D1%7D%5Et%20%5Cbeta1%5E%7Bt-i%7D%20%5Cboldsymbol%7Bg%7D_i)。将过去各时间步小批量随机梯度的权值相加，得到 %20%5Csum%7Bi%3D1%7D%5Et%20%5Cbeta1%5E%7Bt-i%7D%20%3D%201%20-%20%5Cbeta_1%5Et#card=math&code=%281-%5Cbeta_1%29%20%5Csum%7Bi%3D1%7D%5Et%20%5Cbeta_1%5E%7Bt-i%7D%20%3D%201%20-%20%5Cbeta_1%5Et)。需要注意的是，当较小时，过去各时间步小批量随机梯度权值之和会较小。例如，当时，。为了消除这样的影响，对于任意时间步，我们可以将再除以，从而使过去各时间步小批量随机梯度权值之和为1。这也叫作偏差修正。在Adam算法中，我们对变量和均作偏差修正：

接下来，Adam算法使用以上偏差修正后的变量和，将模型参数中每个元素的学习率通过按元素运算重新调整：

其中是学习率，是为了维持数值稳定性而添加的常数，如。和AdaGrad算法、RMSProp算法以及AdaDelta算法一样，目标函数自变量中每个元素都分别拥有自己的学习率。最后，使用迭代自变量：

7.8.2 从零开始实现

我们按照Adam算法中的公式实现该算法。其中时间步通过hyperparams参数传入adam函数。

%matplotlib inline
import torch
import sys
sys.path.append("..") 
import d2lzh_pytorch as d2l
features, labels = d2l.get_data_ch7()
def init_adam_states():
    v_w, v_b = torch.zeros((features.shape[1], 1), dtype=torch.float32), torch.zeros(1, dtype=torch.float32)
    s_w, s_b = torch.zeros((features.shape[1], 1), dtype=torch.float32), torch.zeros(1, dtype=torch.float32)
    return ((v_w, s_w), (v_b, s_b))
def adam(params, states, hyperparams):
    beta1, beta2, eps = 0.9, 0.999, 1e-6
    for p, (v, s) in zip(params, states):
        v[:] = beta1 * v + (1 - beta1) * p.grad.data
        s[:] = beta2 * s + (1 - beta2) * p.grad.data**2
        v_bias_corr = v / (1 - beta1 ** hyperparams['t'])
        s_bias_corr = s / (1 - beta2 ** hyperparams['t'])
        p.data -= hyperparams['lr'] * v_bias_corr / (torch.sqrt(s_bias_corr) + eps)
    hyperparams['t'] += 1

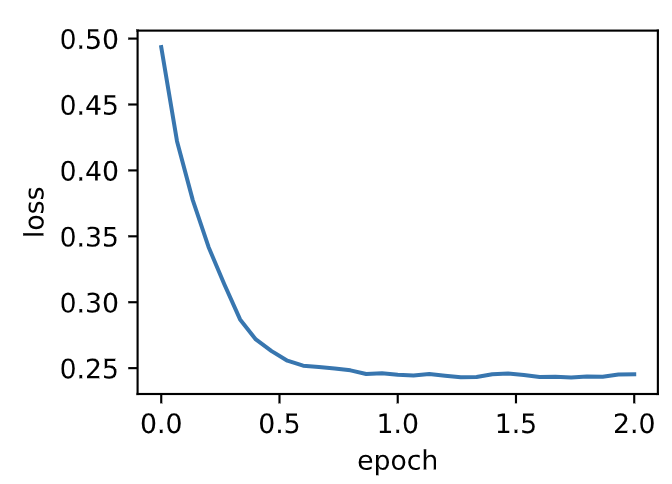
使用学习率为0.01的Adam算法来训练模型。

d2l.train_ch7(adam, init_adam_states(), {'lr': 0.01, 't': 1}, features, labels)

输出：

loss: 0.245370, 0.065155 sec per epoch

7.8.3 简洁实现

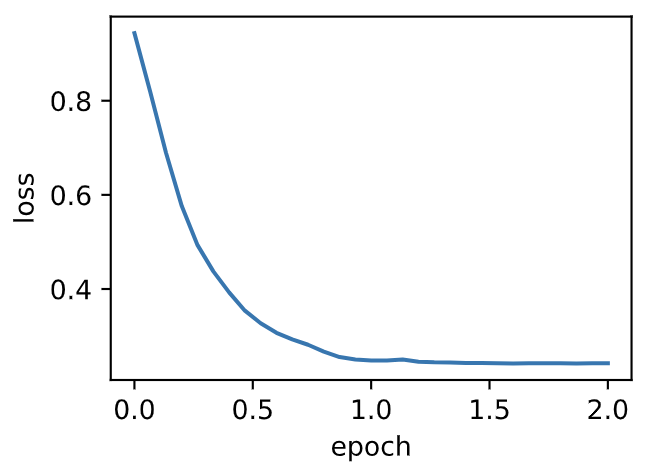
通过名称为“Adam”的优化器实例，我们便可使用PyTorch提供的Adam算法。

d2l.train_pytorch_ch7(torch.optim.Adam, {'lr': 0.01}, features, labels)

输出：

loss: 0.242066, 0.056867 sec per epoch

小结

• Adam算法在RMSProp算法的基础上对小批量随机梯度也做了指数加权移动平均。
• Adam算法使用了偏差修正。

参考文献

[1] Kingma, D. P., & Ba, J. (2014). Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.

注：除代码外本节与原书此节基本相同，原书传送门