1. 简介

举个例子

简略介绍一下 桶排序是怎么玩的

  • 设现在有数组
    1. [29,25,3,49,9,37,21,43]
  1. 通过某种映射关系, 将元素都放入一组有序的桶中 (这个映射关系要保证前面桶中的任何元素都要比后面桶中的任何元素小)

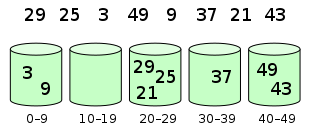
image.png

  1. 如果桶中的元素足够少, 可以直接进行排序

image.png

  1. 最终再将所有桶元素拿出来就是有序的了

简介

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效，我们需要做到这两点：

  1. 在额外空间充足的情况下，尽量增大桶的数量
  2. 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中

同时，对于桶中元素的排序，选择何种比较排序算法对于性能的影响至关重要。

2. 实现

Java实现

这里我就直接抄网上的了

  1. public class BucketSort implements IArraySort {
  3.     private static final InsertSort insertSort = new InsertSort();
  5.     @Override
  6.     public int[] sort(int[] sourceArray) throws Exception {
  7.         // 对 arr 进行拷贝，不改变参数内容
  8.         int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
  10.         return bucketSort(arr, 5);
  11.     }
  13.     private int[] bucketSort(int[] arr, int bucketSize) throws Exception {
  14.         if (arr.length == 0) {
  15.             return arr;
  16.         }
  18.         int minValue = arr[0];
  19.         int maxValue = arr[0];
  20.         for (int value : arr) {
  21.             if (value < minValue) {
  22.                 minValue = value;
  23.             } else if (value > maxValue) {
  24.                 maxValue = value;
  25.             }
  26.         }
  28.         int bucketCount = (int) Math.floor((maxValue - minValue) / bucketSize) + 1;
  29.         int[][] buckets = new int[bucketCount][0];
  31.         // 利用映射函数将数据分配到各个桶中
  32.         for (int i = 0; i < arr.length; i++) {
  33.             int index = (int) Math.floor((arr[i] - minValue) / bucketSize);
  34.             buckets[index] = arrAppend(buckets[index], arr[i]);
  35.         }
  37.         int arrIndex = 0;
  38.         for (int[] bucket : buckets) {
  39.             if (bucket.length <= 0) {
  40.                 continue;
  41.             }
  42.             // 对每个桶进行排序，这里使用了插入排序
  43.             bucket = insertSort.sort(bucket);
  44.             for (int value : bucket) {
  45.                 arr[arrIndex++] = value;
  46.             }
  47.         }
  49.         return arr;
  50.     }
  52.     /**
  53.      * 自动扩容，并保存数据
  54.      *
  55.      * @param arr
  56.      * @param value
  57.      */
  58.     private int[] arrAppend(int[] arr, int value) {
  59.         arr = Arrays.copyOf(arr, arr.length + 1);
  60.         arr[arr.length - 1] = value;
  61.         return arr;
  62.     }
  63. }

3. 分析

时间复杂度

设:

  • 数据有n条, 桶有m个, 平均每个桶有k=n/m个元素;
  • 假设桶内部使用快速排序, 则一个桶的排序时间为O(k*logk)
  • m个桶的时间复杂度就是 O(mklogk)
  • 因为k=n/m; 桶排序的复杂度就是 O(n*log(n/m))
  • 当k=n/m; k比较稳定的时候, 可以近似的把k看做一个常量c, 那么 logc 也是个常量
  • 则最终桶排序的时间复杂度为: O(n)

空间复杂度

  • O(n)

看起来很美妙

虽然从时间复杂度上来看, 这个时间复杂度无敌啊! 但是为什么各种类库不使用它呢?

因为它要想达到理想中的时间复杂度 O(n)必须要满足几个条件

  • 数据要很容易就能划分成m个桶
  • 数据在所有桶中分布比较均匀
  • 桶之间有着天然的大小顺序


使用场景

虽然限制条件比较苛刻, 但桶排序还是有它使用的场景的

  • 外部排序: 桶排序普遍针对数据量很大，无法一次加载进内存的数据, 则排序可以在硬盘上进行, 如果某个区间内数据量仍超出内存，则继续拆分