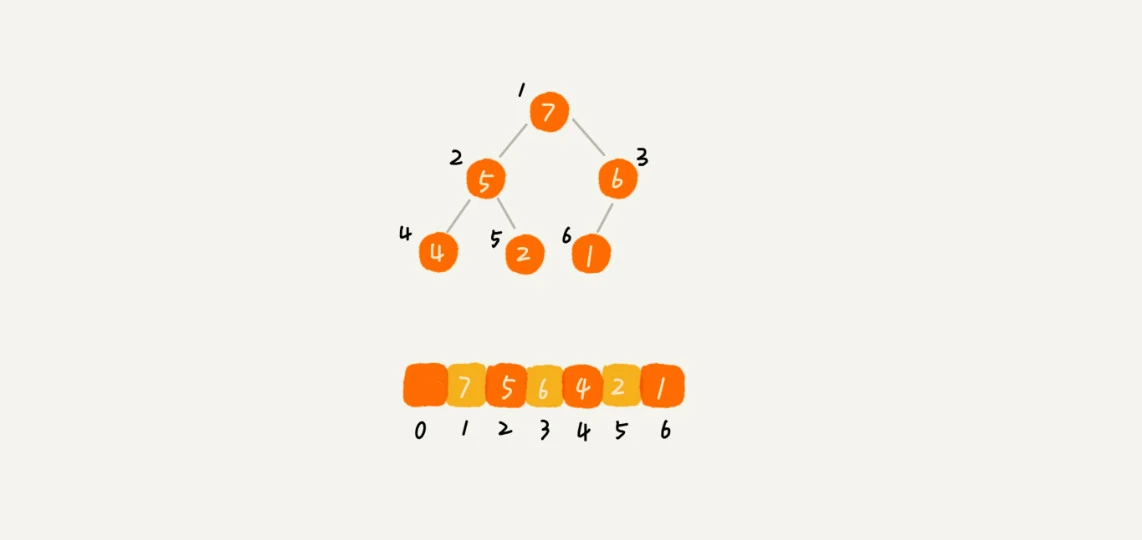1. 简介

堆排序是依赖 堆 这种数据结构设计的一种排序算法。

1.1 堆heap

https://en.wikipedia.org/wiki/Heap_(data_structure))

堆 是一个完全二叉树的结构, 这里用大顶堆举例
它有这几个性质

  1. 即子结点的键值或索引总是小于它的父节点
  2. 对顶在序列第一位
  3. 假设当前元素的索引位置为 i，可以得到规律：
  • parent(i) = i/2（向下取整）
  • left child(i) = 2*i
  • right child(i) = 2*i +1

image.png

2 实现

实现思路

  1. 利用所有元素创建一个大顶堆; 也叫建堆时间复杂度O(n)
  2. 循环执行, 直至堆只剩一个元素:
  • 堆首弹出, 将弹出的元素放到堆的尾部(不在堆内) O(1)
  • 维护最大堆 O(logn)

Java实现

  1. public int[] sort(int[] arr) throws Exception {
  2.     int len = arr.length;
  3.     buildMaxHeap(arr, len);//构建大顶堆
  4.     for (int i = len - 1; i > 0; i--) {
  5.         swap(arr, 0, i);//将堆顶元素移动到堆尾
  6.         len--;
  7.         heapify(arr, 0, len);//重新构建大顶堆
  8.     }
  9.     return arr;
  10. }
  1. //初始化构建大顶堆
  2. private void buildMaxHeap(int[] arr, int len) {
  3.     for (int i = (int) Math.floor(len / 2); i >= 0; i--) {
  4.         heapify(arr, i, len);
  5.     }
  6. }
  1. //堆化
  2. private void heapify(int[] arr, int i, int len) {
  3.     int left = 2 * i + 1;
  4.     int right = 2 * i + 2;
  5.     int largest = i;
  7.     if (left < len && arr[left] > arr[largest]) {
  8.         largest = left;
  9.     }
  11.     if (right < len && arr[right] > arr[largest]) {
  12.         largest = right;
  13.     }
  15.     if (largest != i) {
  16.         swap(arr, i, largest);
  17.         heapify(arr, largest, len);
  18.     }
  19. }

3. 复杂度

时间复杂度:

  • O(nlogn)

空间复杂度:

  • O(1)