1. 简介

实际上学习归并排序最重要的不是为了把这个排序算法学会, 而是学会归并排序用到的思想: 分治法

《算法导论》这本书介绍的第二个算法就是归并排序
书中借由归并排序向大家介绍了一种算法设计的范式分治法

1.1 分治法的思想

将原问题分解为几个规模较小但类似于原问题的子问题, 递归地求解这些子问题, 然后再合并这些子问题的解, 建立原问题的解
分治模式在每层递归时都有三个步骤:

1. 分解: 将原问题分解为若干子问题
2. 解决: 解决这些子问题
3. 合并: 将子问题的解合并, 形成原问题的解

1.2 归并排序的思想

归并排序是个非常典型的分治法排序算法
每一层递归的操作如下:

1. 分解: 将待排序的元素分解成两份
2. 解决: 使用归并排序递归的排序两个子序列
3. 合并: 合并两个已排序的子序列, 使得待排序的元素有序

2. 实现

Java实现

public static int[] sort(int[] sourceArray) {
    int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
    if (arr.length < 2) {
        return arr;
    }
    //分解
    int middle = (int) Math.floor(arr.length / 2);
    int[] left = Arrays.copyOfRange(arr, 0, middle);
    int[] right = Arrays.copyOfRange(arr, middle, arr.length);
    //sort(): 解决
    //merge(): 合并
    return merge(sort(left), sort(right));
}
private static int[] merge(int[] left, int[] right) {
    int[] result = new int[left.length + right.length];
    int i = 0;
    while (left.length > 0 && right.length > 0) {
        if (left[0] <= right[0]) {
            result[i++] = left[0];
            left = Arrays.copyOfRange(left, 1, left.length);
        } else {
            result[i++] = right[0];
            right = Arrays.copyOfRange(right, 1, right.length);
        }
    }
    while (left.length > 0) {
        result[i++] = left[0];
        left = Arrays.copyOfRange(left, 1, left.length);
    }
    while (right.length > 0) {
        result[i++] = right[0];
        right = Arrays.copyOfRange(right, 1, right.length);
    }
    return result;
}

3. 简单分析

时间复杂度

• 归并排序的时间复杂度为O(nlog(n))

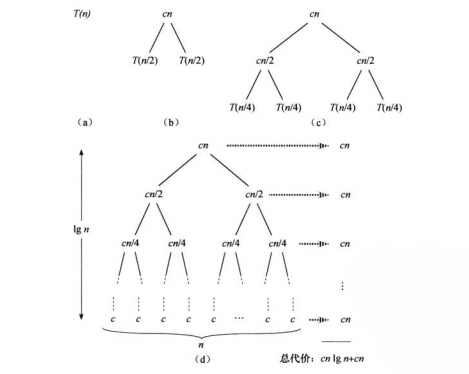
• 树高 logn, 每一层要处理的元素有n个, 所以总的时间复杂度为 nlogn

空间复杂度

• 由于排序的每个子任务都需要使用额外的内存空间, 所以控件复杂度是O(n)

稳定性

• 归并排序不会因为元素的排列顺序而影响排序的速度
• 至今JDK中都还有归并排序存在, 就足以说明归并排序的算法足够稳定

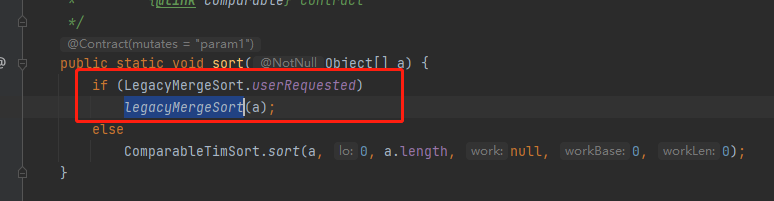
感兴趣的可以看看java.util.Arrays#sort(java.lang.Object[])这个排序算法的注释

 * <p>This sort is guaranteed to be <i>stable</i>:  equal elements will
 * not be reordered as a result of the sort.