【实战】动态规划之完全背包问题相关例题

LeetCode#518： Coin Change 2

Question

You are given coins of different denominations and a total amount of money. Write a function to compute the number of combinations the make up the amount. You may assume that you have infinite number of each kind of coin.

Example 1:

Input: amount = 5, coins = [1, 2, 5]
Output: 4
Explanation: there are four ways to make up the amount:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

Example 2:

Input: amount = 3, coins = [2]
Output: 0
Explanation: the amount of 3 cannot be made up just with coins of 2.

Example 3:

Input: amount = 10, coins = [10] 
Output: 1

Note:

You can assume that

• 0 <= amount <= 5000
• 1 <= coin <= 5000
• the number of coins is less than 500
• the answer is guaranteed to fit into signed 32-bit integer

Solution

复习完全背包问题

“完全背包”问题是 “0-1” 背包问题的扩展，其特点以及其与 0-1 背包问题的区别主要在于：

• “完全背包”问题的特点是：背包里的物品可以无限次选取；
• 本题特殊的地方在于：从背包里选取的物品必须刚好装满需要考虑的容量，而不是小于等于，注意这一点细微的区别。
• “0-1”背包问题：当前考虑的物品拿或者不拿；
• “完全背包问题”：当前考虑的物品拿或者不拿，如果拿，只要背包能装下，就可以一直拿，直到背包装不下为止。

求解思路依然是：一个一个物品考虑，容量一点一点扩大，整个过程是一个 尝试 和 比较 的过程。

思考状态和状态转移方程

• 第 1 步：定义状态
  dp[i][j]：硬币列表的前缀区间 [0, j] 能够凑成总金额为 j 的组合数。
  说明：背包问题有一个特点，顺序无关，在本题解的最开始，我们强调过这道问题的这个性质，因此可以一个一个硬币去考虑。
• 第 2 步：状态转移方程（基础状态转移方程，本题解的后半部分有优化）
  对于遍历到的每一种面值的硬币，逐个考虑添加到“总金额”中。由于硬币的个数可以无限选取，因此对于一种新的面值的硬币 coin[i]，一次考虑选取 0 枚、1枚、2枚，以此类推，只要选取这种面值的硬币的总金额超过需要的总金额 j 为止。
  状态转移方程：``` dp[i][j] = dp[i - 1][j - 0 * coins[i]] +

        dp[i - 1][j - 1 * coins[i]] +
        dp[i - 1][j - 2 * coins[i]] +
        ... +
        dp[i - 1][j - k * coins[i]];

  `` <br />说明：状态转移方程基于“分类计数原理”：完成一件事，有 n 类办法，在第 1 类办法中有 ![](https://g.yuque.com/gr/latex?m_1#card=math&code=m_1) 种不同的方法，在第 2 类办法中有 ![](https://g.yuque.com/gr/latex?m_2#card=math&code=m_2) 种不同的方法，......，在第 n 类办法中有 ![](https://g.yuque.com/gr/latex?m_n#card=math&code=m_n) 种不同的方法，那么完成这件事共有：![](https://g.yuque.com/gr/latex?N%20%3D%20m_1%20%2B%20m_2%20%2B%20......%20%2B%20m_n#card=math&code=N%20%3D%20m_1%20%2B%20m_2%20%2B%20......%20%2B%20m_n) 种不同的办法。<br />上述公式需要满足：j - k * coins[i] >= 0。dp[i][j]相对于dp[i - 1][j]而言，多考虑的一枚硬币，是当前正在考虑的那枚硬币的面值，coins[i]，而这枚硬币选取的个数（从 0 开始）就是dp[i][j]` 这个问题可以分解的各个子问题的分类标准。
• 第 3 步：思考初始化
  dp[0][0] 的值设置为 1，这一点可能比较难以理解，但它作为被参考的值，可以使得后续的状态转移方程正确。原因是：当dp[i - 1][j - k * coins[i]] 的第 2 维j - k * coins[i] == 0成立的时候，k 个硬币 coin[i] 恰好成为了一种组合。因此，dp[0][0] = 1 是合理的（代入状态方程，值正确）。
  填写第 1 行（下标为 0 的那一行），也是初始化的时候需要考虑的内容。第 1 行只考虑第 1 枚硬币 coins[0]，能够组合出的容量只有 coins[0] 的整数倍数。
• 第 4 步：思考输出
  输出就是表格的最后一格的值，即dp[len - 1][amount]。
• 第 5 步：考虑空间优化
  当前状态行的值，只和上一行的状态值相关，可以使用滚动数组技巧。一个更经典的空间优化的方法是采用和 0-1 背包问题相对的赋值的方式，我们留在本题的后半部分再介绍。

参考代码1：

class Solution {
    public int change(int amount, int[] coins) {
        if (coins == null || coins.length == 0) {
            if (amount == 0) {
                return 1;
            }
            return 0;
        }
        int len = coins.length;
        int[][] dp = new int[len][amount + 1];
        // 初始化
        dp[0][0] = 1;
        for (int i = coins[0]; i <= amount; i += coins[0]) {
            dp[0][i] = 1;
        }
        for (int i = 1; i < len; i++) { //i表示可以选择[0, i]区间内硬币
            for (int j = 0; j <= amount; j++) { // j表示金额
                for (int k = 0; j - k * coins[i] >= 0; k++) {
                    dp[i][j] += dp[i - 1][j - k * coins[i]];
                }
            }
        }
        return dp[len-1][amount];
    }
}

复杂度分析：

• 时间复杂度：#card=math&code=O%28NM%5E2%29)，这里金额为 M，硬币数为 。第 1 层循环与硬币总数的规模 相同，第 2 层循环与要求的总金额的规模 相同，第 3 层循环在 最坏情况下，硬币的面值为 1 时，与要求的总金额的规模 相同；
• 空间复杂度：#card=math&code=O%28NM%29)，dp 表格有 行， 列。

补充：使用“滚动数组”技巧

如果使用“滚动数组”，当前行的值应该先恢复到 0，这是因为上一行在 j - k * coins[i] >= 0 的时候才计算结果，上一行后面的部分没有计算就直接到下一行了。

如果直接使用“滚动数组”的话，就有可能引用到错误的结果。想象一下填表的过程，如果不设置为0，就有可能引用到错误的结果。也就是说，在填表的时候，不是每一格都会计算结果去覆盖掉原先的值，这个细节如果不好想明白，可以在纸上模拟一次填表的过程。

参考代码2：

class Solution {
    public int change(int amount, int[] coins) {
        if (coins == null || coins.length == 0) {
            if (amount == 0) {
                return 1;
            }
            return 0;
        }
        int len = coins.length;
        int[][] dp = new int[2][amount + 1];
        dp[0][0] = 1;
        for (int i = coins[0]; i <= amount; i += coins[0]) {
            dp[0][i] = 1;
        }
        for (int i = 1; i < len; i++) {
            // 注意：如果写成滚动数组的情况，这一行完全参考上一行的值
            // 当前行的值应该先设置为 0，这是因为上一行只在 j - k * coins[i] >= 0 的时候才计算结果，
            // 后面的部分程序没有计算直接跳到下一行了
            // 如果不清空为 0，就有可能引用到错误的结果
            Arrays.fill(dp[i & 1], 0);
            for (int j = amount; j >= 0; j--) {
                for (int k = 0; j - k * coins[i] >= 0; k++) {
                    dp[i & 1][j] += dp[(i - 1) & 1][j - k * coins[i]];
                }
            }
        }
        return dp[(len - 1) & 1][amount];
    }
}

事实上，上述状态转移方程做了很多重复的工作，还可以优化。

优化状态转移方程（重点）

根据状态转移方程其实可以得到递推公式。状态转移方程的表示形式看起来就像一个无穷级数，可以通过如下方式得到如下递推方式：

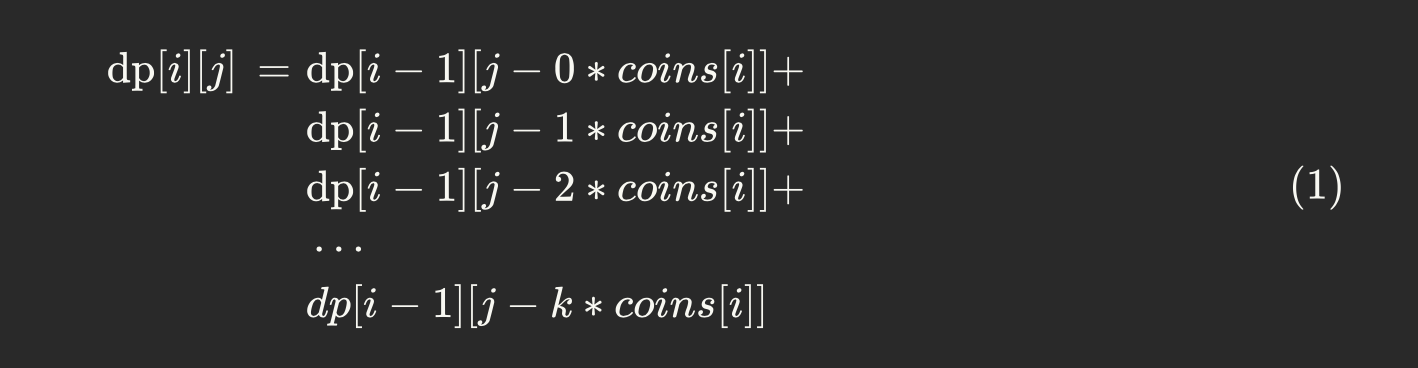
这里 j - k * coins[i] >= 0。将 j 用 coins[i] 替换，得：

这里 j - coins[i] - k * coins[i] >= 0。整理得：

这里 j - k * coins[i] >= 0。

将等式 (1) - 等式 (3)，得：

%0A#card=math&code=dp%5Bi%5D%5Bj%5D%20-%20dp%5Bi%5D%5Bj%20-%20coins%5Bi%5D%5D%20%3D%20dp%5Bi%20-%201%5D%5Bj%5D%20%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%284%29%0A)

整理得：

%0A#card=math&code=dp%5Bi%5D%5Bj%5D%20%3D%20dp%5Bi%20-%201%5D%5Bj%5D%20%2B%20dp%5Bi%5D%5Bj%20-%20coins%5Bi%5D%5D%0A%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%5Cspace%285%29%0A)

所以其实每一行单元的值的填写只要看它的左边的值。如果没有左边，它至少是上一行单元格的值。

参考代码3：

class Solution {
    public int change(int amount, int[] coins) {
        int len = coins.length;
        if (len == 0) {
            if (amount == 0) {
                return 1;
            }
            return 0;
        }
        int[][] dp = new int[len][amount + 1];
        dp[0][0] = 1;
        for (int i = coins[0]; i <= amount; i += coins[0]) {
            dp[0][i] = 1;
        }
        for (int i = 1; i < len; i++) {
            for (int j = 0; j <= amount; j++) {
                dp[i][j] = dp[i - 1][j];
                if (j - coins[i] >= 0) {
                    dp[i][j] += dp[i][j - coins[i]];
                }
            }
        }
        return dp[len - 1][amount];
    }
}

复杂度分析：

• 时间复杂度：#card=math&code=O%28NM%29)，这里金额为 ，硬币数为 。与参考代码 1 相比缩减了最内层的循环，时间复杂度降低了一级；
• 空间复杂度：#card=math&code=O%28NM%29)，表格有 行， 列。

考虑空间优化（重要）：

由状态转移方程（5）知道，当前状态值参考了当前行前面的值，因此将空间优化到一维表格的时候，正序遍历是合理的。

参考代码3：

class Solution {
    public int change(int amount, int[] coins) {
        int len = coins.length;
        if (len == 0) {
            if (amount == 0) {
                return 1;
            }
            return 0;
        }
        int[] dp = new int[amount + 1];
        dp[0] = 1;
        for (int i = coins[0]; i <= amount; i += coins[0]) {
            dp[i] = 1;
        }
        for (int i = 1; i < len; i++) {
            // 从 coins[i] 开始即可
            for (int j = coins[i] ; j <= amount; j++) {
                dp[j] += dp[j - coins[i]];
            }
        }
        return dp[amount];
    }
}

复杂度分析：

• 时间复杂度：#card=math&code=O%28NM%29)，这里金额为 ，硬件数为 ；
• 空间复杂度：#card=math&code=O%28M%29)，表格只有 1 行， 列。