【理论】二叉搜索树基础

一、二叉搜索树

1. 二叉树搜索基本实现

public class BST {
    private Node root;
    private int count;
    public BST() {
        root == null;
        count = 0;
    }
    public int size() {
        return count;
    }
    public boolean isEmpty() {
        return count == 0;
    }
    class Node {
        private int key;
        private int value;
        private Node left;
        private Node right;
        public Node(int key, int value) {
            this.key = key;
            this.value = value;
            this.left = null;
            this.right = null;
        }
    }
}

2. 二叉搜索树结点插入

思路：我们应该充分利用二叉搜索树的特点来完成 insert 操作的编写。

/**
 *
 * @param key
 * @param value
 */
public void insert(K key, V value) {
    root = insert(root, key, value);
}
/**
 * 在以 node 为结点的二分搜索树中插入结点(key, value)
 * 返回插入(key, value) 的二分搜索树的根
 * (1) count++ 别忘了
 * (2) 要把 node 返回回去
 */
private Node insert(Node node, K key, V value) {
    if (node == null) {
        count++;
        return new Node(key, value);
    } else if (node.key.compareTo(key) == 0) {
        node.value = value;
        return node;
    } else if (key.compareTo(node.key) > 0) {
        node.right = insert(node.right, key, value);
        return node;
    } else {
        node.left = insert(node.left, key, value);
        return node;
    }
}

3. 二叉搜索树的查找

查找专注于找到这个元素。我们思考一下，在 search 这个方法中，我们应该将什么返回回去，一个好的数据结构应该将内部的数据对外隐藏。

二分查找树的包含 contain(返回 true 或者 false) 和查找 search （返回相应的 value 值）同质。

考虑查找成功和失败这两种情况。

3.1 contain 函数

/**
 * 在整个二叉树中是否包含 key
 */
public boolean contain(int key) {
    return contain(root, key);
}
public boolean contain(Node node, int key) {
    if (node == null) {
        return false;
    }
    if (key == node.key) {
        return true;
    } else if (key < root.key) {
        return contain(node.left, key);
    } else {
        return contain(node.right, key);
    }
}

3.2 search 函数

// serach 的返回值是什么，这是一个设计问题
// 可以返回 Node，返回 value
public int search(int key) {
    return search(root, key);
}
/**
 * 在以 node 为根的二叉搜索树中查找 key 所对应的 value
 */
private Integer search(Node node, int key) {
    if (node == null) {
        return null;
    }
    if (key == node.key) {
        return node.value;
    } else if (key < node.key) {
        return search(node.left, key);
    } else {
        return search(node.right, key);
    }
}

二、树的遍历

1. 前、中与后序遍历

1.1 递归实现

// 对以 node 为根的二叉树搜索树进行前序遍历
public void preOrder(Node node) {
    if (node != null) {
        System.out.println(node.key);
        preOrder(node.left);
        preOrder(node.right);
    }
}
// 对以 node 为根的二叉搜索树进行中序遍历
public void inOrder(Node node) {
    if (node != null) {
        inOrder(node.left);
        System.out.println(node.key);
        inOrder(node.right);
    }
}
// 对以 node 为根的二叉搜索树进行后序遍历
public void postOrder(Node node) {
    if (node != null) {
        postOrder(node.left);
        postOrder(node.right);
        System.out.println(node.key);
    }
}

2. 层序遍历（广度优先）

基于队列实现

public void levelOrder() {
    Queue<Node> queue = new ArrayDeque<>();
    while (!queue.isEmpty()) {
        Node node = queue.poll();
        System.out.println(node.key);
        if (node.left != null) {
            queue.add(node.left);
        }
        if (node.right != null) {
            queue.add(node.right);
        }
    }
}

三、二叉搜索树的删除

1. 删除最大/小值

1.1 删除最小值

/**
 * 寻找最小的 key
 */
public int minimum() {
    assert count != 0;
    Node minimum = minimum(root);
    return minimum.key;
}
public Node minimum(Node node) {
    if (node.left == null) {
        return node;
    }
    return minimum(node.left);
}
/**
 * 从二分搜索树中删除最小 key 所在的结点
 */
public void removeMin() {
    if (root != null) {
        root = removeMin(root);
    }
}
/**
 * 删除以 node 为根的二分搜索树中的最小的结点
 * 返回删除结点后新的二分搜索树的根
 * 
 * @param node
 * @return
 */
private Node removeMin(Node node) {
    if (node.left == null) {
        // 就是删除这个结点 node
        Node rightNode = node.right;
        node.right = null;
        count--;
        return rightNode;
    }
    node.left = removeMin(node.left);
    return node;
}

1.2 删除最大值

/**
 * 寻找最大的 key
 */
public int maximum() {
    assert count != 0;
    Node maximum = maximum(root);
    return maximum.key;
}
public Node maximum(Node node) {
    assert count != 0;
    // 只要是递归就要处理递归到底的情况
    if (node.right == null) {
        return node;
    }
    return maximum(node.right);
}
public void removeMax() {
   if (root != null) {
       root = removeMax(root);
   } 
}
public Node    removeMax(Node node) {
    if (node.right == null) {
        Node leftNode = node.left;
        node.left = null;
        count--;
        return leftNode;
    } else {
        node.right = removeMax(node.right);
        return node;
    }
}

2. 删除任意结点

四、二叉搜索树的顺序性与局限性

1. 顺序性

二分搜索树当做查找表的一种实现。我们使用二分搜索树的目的是通过查找 key 马上得到 value。

2. 局限性

二分查找树的性能。二分查找树在一些极端情况下性能并不好。
我们首先要认识下面一个事实：同样的数据，可以对应不同的二分搜索树。看下面的例子。

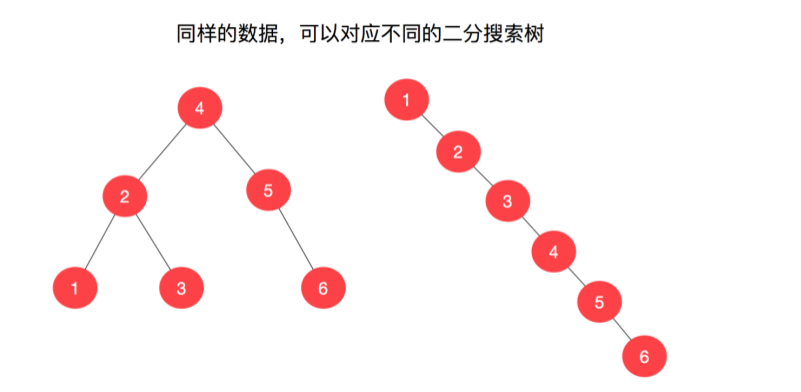
二分搜索树可以退化为链表。此时时间复杂度变成了 O(n)。
极端测试：如果把 key 排序好以后，依次插入到二分搜索树中，此时二分搜索树的高度就会变得非常高。

解决方案：平衡二叉树，使用红黑树（红黑树是一种平衡二叉树的实现，其它平衡二叉树的实现还有 2-3 tree，AVL tree，Splay tree，平衡二叉树和堆的结合：Treap）。左右两棵子树的高度差不会超过1。

解决方案：平衡二叉树，使用红黑树（红黑树是一种平衡二叉树的实现，其他平衡二叉树的实现还有 2-3 tree，AVL tree，Splay tree，平衡二叉树和堆的结合：Treap）。左右两颗子树的高度差不会超过 1。

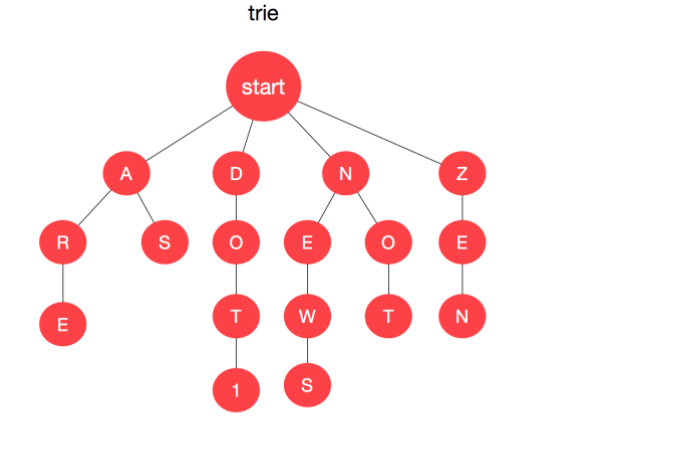
trie。使用 trie 统计词频。

五、树形问题和更多树

解题的时候要利用好树的特性，

首先几个遍历一定要掌握好，基本上成功的遍历可以将二叉树压成链表来看，复杂度进一步降低。除此之外，二叉搜索树的特性也要考虑到。

此外，有些问题虽然没有直接创建树。但是却是和数离不开的。

递归方法天然地具有递归的性质。

归并排序法和快速排序法的思想它们像极了对一棵树进行后序遍历和前序遍历。

• 搜索问题；
• 一条龙游戏；
• 8 数码；
• 8 皇后；
• 数独；
• 搬运工；
• 人工智能：搬运工，树形搜索；
• 机器学习；
• 更多树：KD 树，区间树，哈夫曼树