6deb3d0f336ca51f3b7f3eff5d0f4477.jpg

今天我们先来学习一下贪心算法（greedy algorithm）。贪心算法有很多经典的应用，比如霍夫曼编码（Huffman Coding）、Prim 和 Kruskal 最小生成树算法、还有 Dijkstra 单源最短路劲算法。最小生成树算法和最短路径算法后面会讲到，今天先讲下霍夫曼编码，看看它是如何利用贪心算法来实现对数据压缩编码，有效节省数据存储空间的。

如何理解“贪心算法”？

关于贪心算法，我们先看一个例子。

假设我们有一个可以容纳 100 kg 物品的背包，可以装各种物品。我们有以下5种豆子，每种豆子的总量和总价值都各不相同。为了让背包中所装物品的总价值最大，我们如何选择在背包中装哪些豆子？每种豆子又该装多少呢？

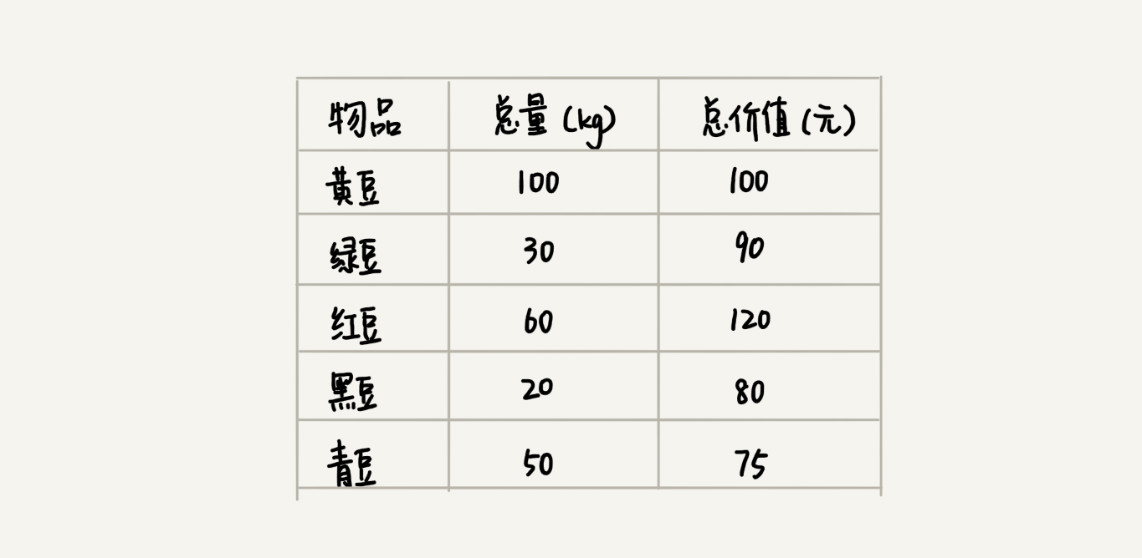
f93f4567168d3bc65688a785b76753c7.jpg

实际上这个问题很简单，估计你一下就能想出来。没错，我们只要先算一算每个物品的单价，按照单价由高到低依次来装就好了。单价从高到低排列，依次是：黑豆、绿豆、红豆、青豆、黄豆，所以，我们可以往背包里装 20 kg 黑豆、30 kg 绿豆、50 kg 红豆。

第一步，当我们看到这类问题的时候，首先要联想到贪心算法：针对一组数据，我们定义了限制值和期望值，希望从中选出几个数据，在满足限制值的情况下，期望值最大。

类比到刚刚的例子，限制值就是重量不能超出 100 kg，期望值就是物品的总价值。这组数据就是5种豆子。我们从中选出一部分，满足重量不超过 100 kg，并且总价值最大。

第二步，我们尝试看下这个问题是否可以用贪心算法解决：每次选择当前价值下，在对限制值同等贡献量的情况下，对期望值贡献最大的数据。

类比到刚刚的例子，我们每次都从剩下的豆子里面，选择单价最高的，也就是重量相同的情况下，对价值贡献最大的豆子。

第三步，我们举几个例子看下贪心算法产生的结果是否是最优的：大部分情况下，举几个例子验证一下就行了。严格地证明贪心算法的正确性，是非常复杂的，需要涉及比较多的数学推理。而且，从实践的角度来说，大部分能用贪心算法解决的问题，贪心算法的正确性都是显而易见的，也不需要严格的数学推导证明。

实际上，用贪心算法解决问题的思路，并不总能给出最优解。

举一个例子。在一个有权图中，我们从顶点 S 开始，找到一条顶点 T 的最短路径（路径中边的权值和最小）。贪心算法的解决思路是。每次都选择一条跟当前顶点相连的权最小的边，直到找到顶点 T。按照这种思路，我们求出的最短路径是 S -> A -> E -> T，路径长度是 1+4+4=9。

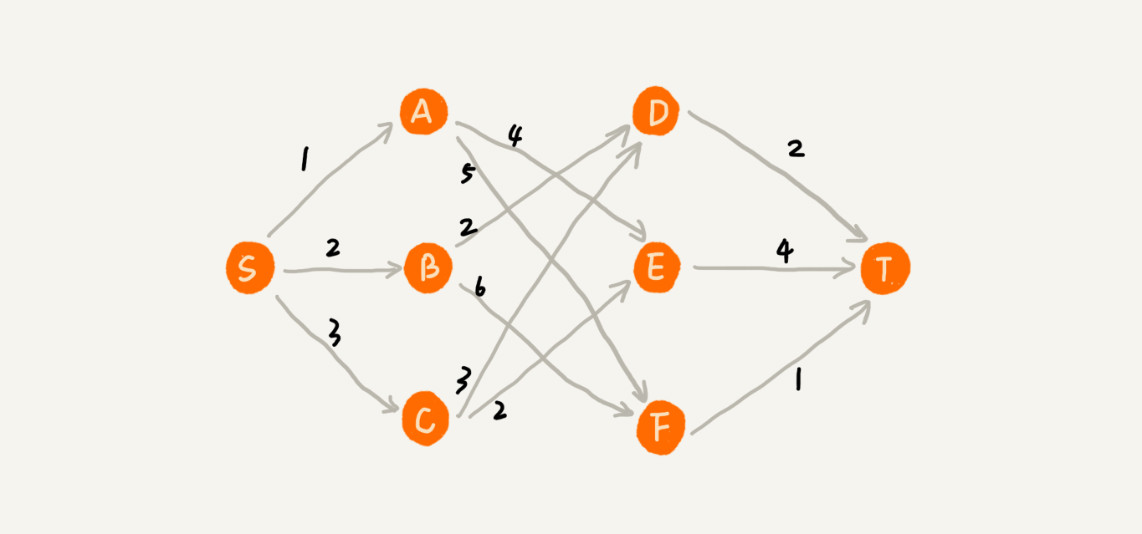
2de91c0afb0912378c5acf32a173f642.jpg

但是，这种贪心的选择方式，最终求的路径并不是最短路径，因为路径 S->B->D->T 才是最短路径，因为这条路径的长度是 2+2+2=6。为什么贪心算法在这个问题上不工作了呢？

在这个问题上，贪心算法不工作的主要原因是，前面的选择，会影响后面的选择。如果我们第一步从顶点 S 走到顶点 A，那接下来面对的顶点和边，跟第一步顶点 S 走到顶点 B，是完全不同的。所以，即便我们第一步选择最优的走法（边最短），但有可能因为这一步选择，导致后面每一步的选择都很糟糕，最终也就无缘全局最优解了。

贪心算法实战分析

对于贪心算法，你是不是还有点懵？如果死抠理论的话，确实很难理解透彻。掌握贪心算法的关键是多练习。只要多练习几道题，自然就有感觉了。所以，接下来就分析几个具体的例子，帮助理解贪心算法。

1. 分糖果

我们有 m 个糖果和 n 个孩子。我们现在要把糖果分给这些孩子吃，但是糖果少，孩子多（m < n），所以糖果只能分配给一部分孩子。

每个糖果的大小不等，这 m 个糖果的大小分别是 s1，s2，s3，……，sm。除此之外，每个孩子对糖果大小的需求也是不一样的，只有糖果的大小大于等于孩子对糖果的需求的时候，孩子才得到满足。假设这 n 个孩子对糖果大小的需求分别是 g1，g2，g3，……，gn。

我的问题是，如何分配糖果，能尽可能满足最多数量的孩子？

我们可以把这个问题抽象成，从 n 个孩子中，抽取一部分分配糖果，让满足的孩子的个数（期望值）是最大的。这个问题的限制值就是糖果个数 m。

我们现在来看看如何用贪心算法来解决。对于一个孩子来说，如果小的糖果可以满足，我们就没必要用更大的糖果，这样更大的就可以留给其他对糖果大小需求更大的孩子。另一方面，对糖果大小需求小的孩子更容易被满足，所以，我们可以从需求小的孩子开始分配糖果。因为满足一个需求大的孩子跟满足一个需求小的孩子，对我们的期望值是一样的。

我们每次从剩下的孩子中，找出对糖果需求最小的，然后发给它剩下的糖果中能满足他的最小的糖果，这样得到的分配方案，也就是满足的孩子个数最多的方案。

2. 钱币找零

这个问题在我们的日常生活中更加普遍。假设我们有 1元、2元、5元、10元、20元、50元、100元这些面额的纸币，它们的张数分别是 c1、c2、c5、c10、c20、c50、c100。我们现在要用这些钱来支付 K 元，最少要用多少张纸币呢？

在生活中，我们肯定是先用面值最大的来支付，如果不够，就继续用更小一点面值的，以此类推，最后剩下的用 1 元来补齐。

在贡献相同期望值（纸币数目）的情况下，我们希望多贡献点金额，这样就可以让纸币数更少，这就是一种贪心算法的解决思路。直觉告诉我们，这种处理方法就是最好的。实际上，要严谨地证明这种贪心算法的正确性，需要比较复杂的、有技巧的数学推导，我不建议你花太多时间在上面，不过如果感兴趣的话，可以自己去研究下。

3. 区间覆盖

假设我们有 n 个区间，区间的起始端点和结束端点分别是[l1, r1]，[l2, r2]，[l3, r3], ……, [ln, rn]。我们从这 n 个区间中选出一部分区间，这部分区间满足两两不相交（端点相交的情况不算相交），最多能选出多少个区间呢？

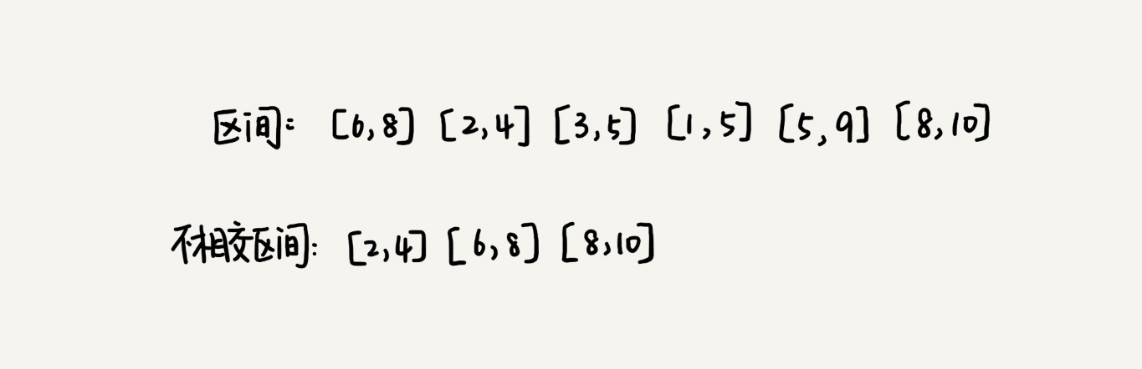
f0a1b7978711651d9f084d19a70805cd.jpg

这个问题的处理思路稍微不是那么好懂，不过，建议你最好能弄懂，因为这个处理思想在很多贪心算法问题中都有用到，比如任务调度、教师排课等等问题。

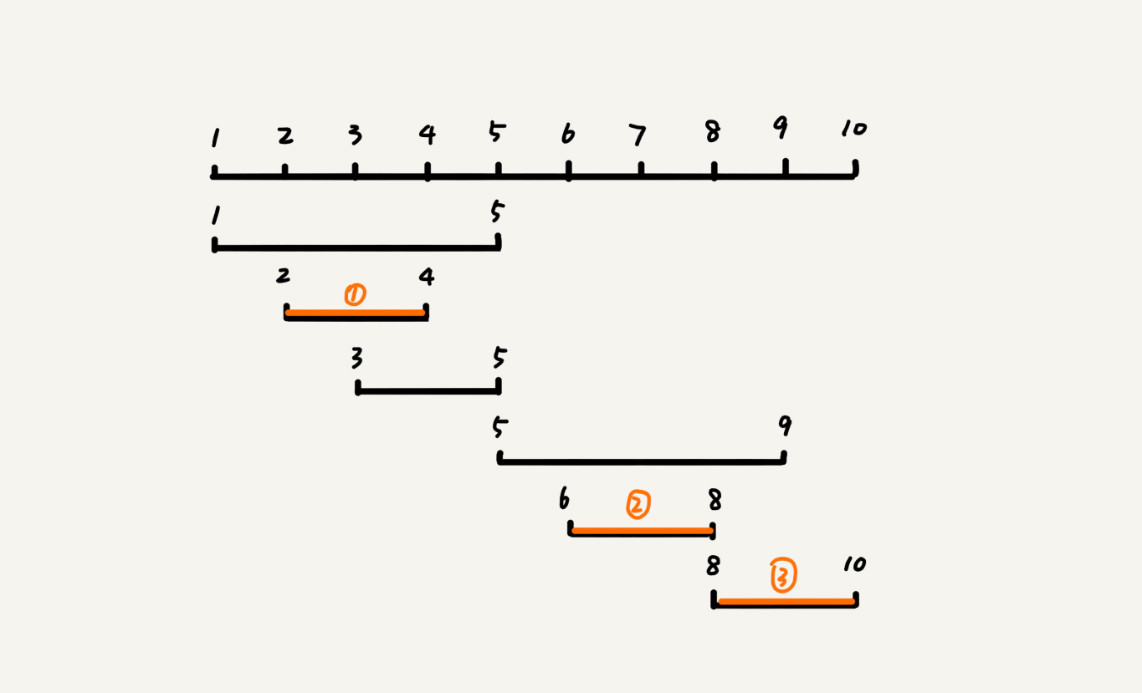
这个问题的解决思路是这样的：我们假设这 n 个区间中最左端是 lmin，最右端点是 rmax。这个问题就相当于，我们选择几个不相交的区间，从左到右将 [lmin, rmax] 覆盖上。我们按照起始端点从小到大的顺序对这 n 个区间排序。

我们每次选择的时候，左端点跟前面的已经覆盖的区间不重合的，右端点又尽量小的，这样可以让剩下的未覆盖区间尽可能的大，就可以放置更多的区间。这实际上就是一种贪心的选择方法。

ef2d0bd8284cb6e69294566a45b0e2b5.jpg

解答开篇

今天的内容就讲完了，我们现在来看开篇的问题，如何用贪心算法实现霍夫曼编码？

假设我有一个包含 1000 个字符的文件，每个字符占 1 个byte（1byte=8bites），存储这1000个字符就一共需要8000 bits，那有没有更加节省空间的存储方式呢？

假设我们通过统计分析发现，这 1000 个字符中只包含 6 种不同字符，假设它们分别是 a、b、c、d、e、f。而 3 个进制位（bit）就可以表示 8 个不同的字符，所以，为了尽量减少存储空间，每个字符我们用 3 个二进制位来表示。那存储这 1000 个字符只需要 3000bits 就可以了，比原来的存储方式节省了很多空间。不过，还有没有更加节省空间的存储方式呢？

  1. a(000)、b(001)、c(010)、d(011)、e(100)、f(101)

霍夫曼编码就要登场了。霍夫曼编码是一种十分有效的编码方式，广泛用于数据压缩中，其压缩率通常在 20% ~ 90%之间。

霍夫曼编码不仅会考察文本中有多少个不同字符，还会考察每个字符出现的频率，根据频率的不同，选择不同长度的编码。霍夫曼编码试图用这种不等长的编码方法，来进一步增加压缩的效率。如何给不同频率的字符选择不同长度的编码呢？根据贪心的思想，我们可以把出现频率比较多的字符，用稍微短一些的编码；出现频率比较少的字符，用稍微长一些的编码。

对于等长的编码来说，我们解压缩起来很简单。比如刚才那个例子中，我们用 3 个 bit 表示一个字符。在解压缩的时候，我们每次从文本中读取 3 位二进制码，然后翻译成对应的字符。但是，霍夫曼编码是不等长的，每次应该读取 1 位还是 2 位、3 位等等来解压缩呢？这个问题就导致霍夫曼编码解压缩起来比较复杂。为了避免解压缩过程中的歧义，霍夫曼编码要求各个字符的编码之间，不会出现某个编码是另一个编码前缀的情况。

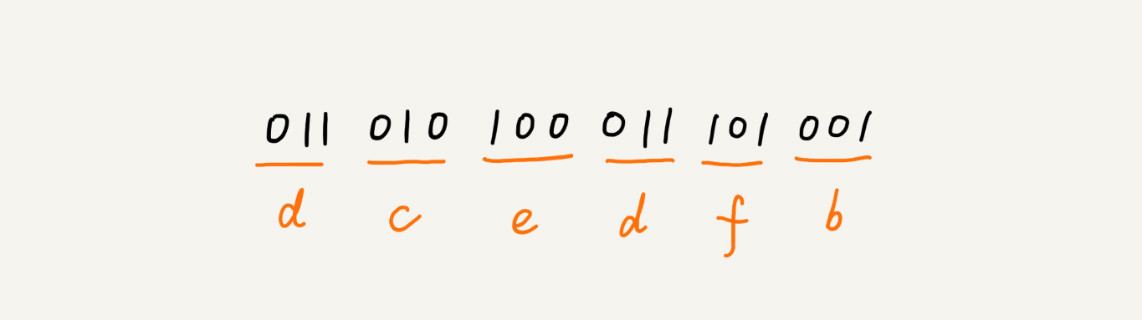
02ad3e02429b294412fb1cff1b3d3829.jpg

假设这 6 个字符出现的频率从高到低依次是 a、b、c、d、e、f。我们把它们编码下面这个样子，任何一个字符的编码都不是另一个的前缀，在解压缩的时候，我们每次会读取尽可能长的可解压的二进制串，所以在解压缩的时候也不会歧义。经过这种编码压缩之后，这 1000 个字符只需要 2100bits 就可以了。

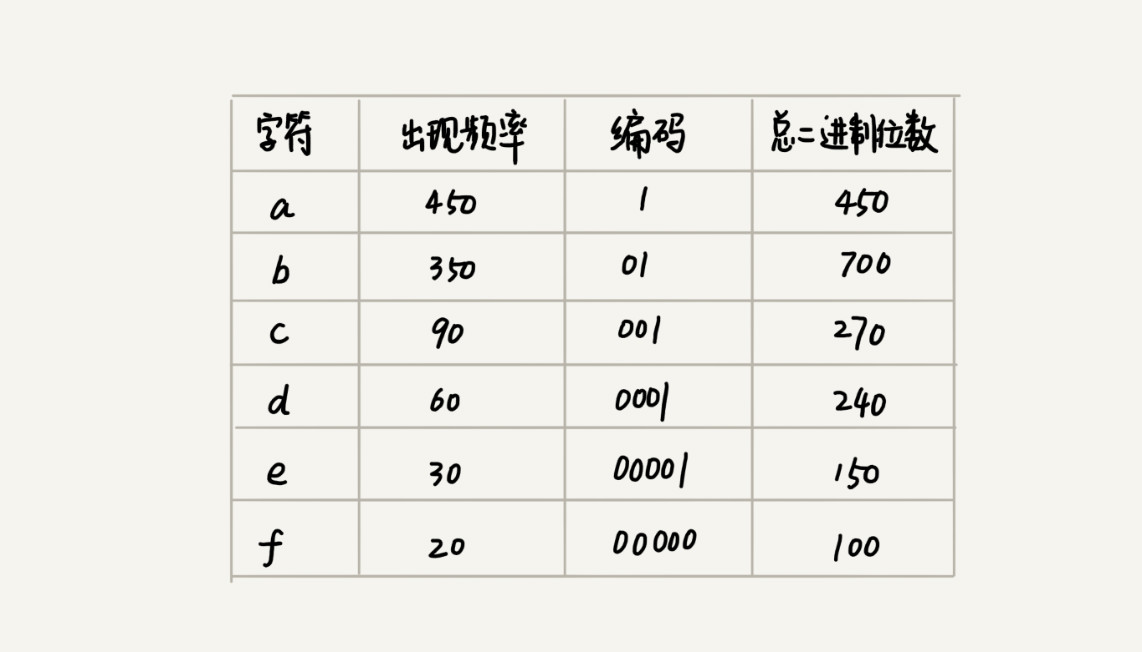
83921e609c8a4dc81ca5b90c8b4cd745.jpg

尽管霍夫曼编码的思想并不难理解，但是如何根据字符出现频率的不同，给不同的字符进行不同长度的编码呢？这里的处理稍微有些技巧。

我们把每个字符看作一个节点，并且附带着把频率放到优先级队列中。我们从队列中取出频率最小的两个节点 A、B，然后新建一个节点 C，把频率设置为两个节点的频率之和，并把这个新节点 C 作为节点 A、B 的父节点。最后再把 C 节点放入到优先级队列中。重复这个过程，直到队列中没有数据。

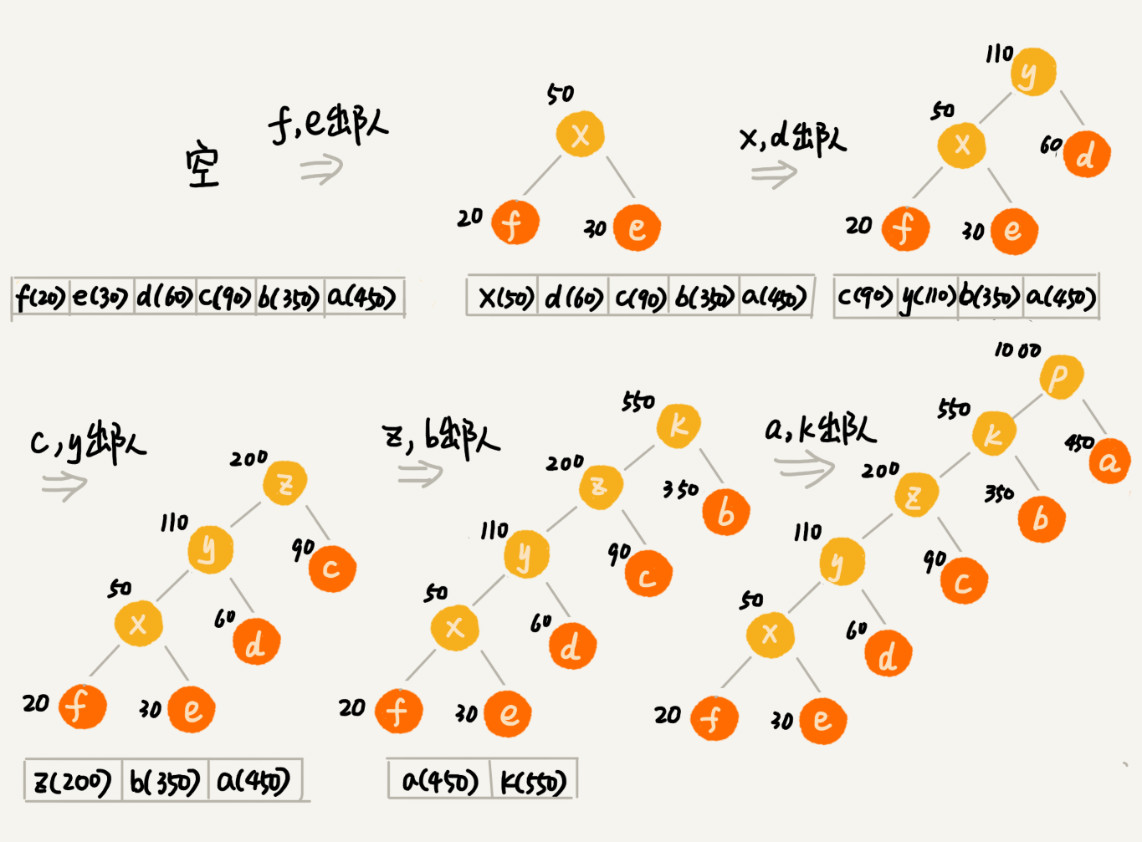
7b6a08e7df45eac66820b959c64f877a.jpg

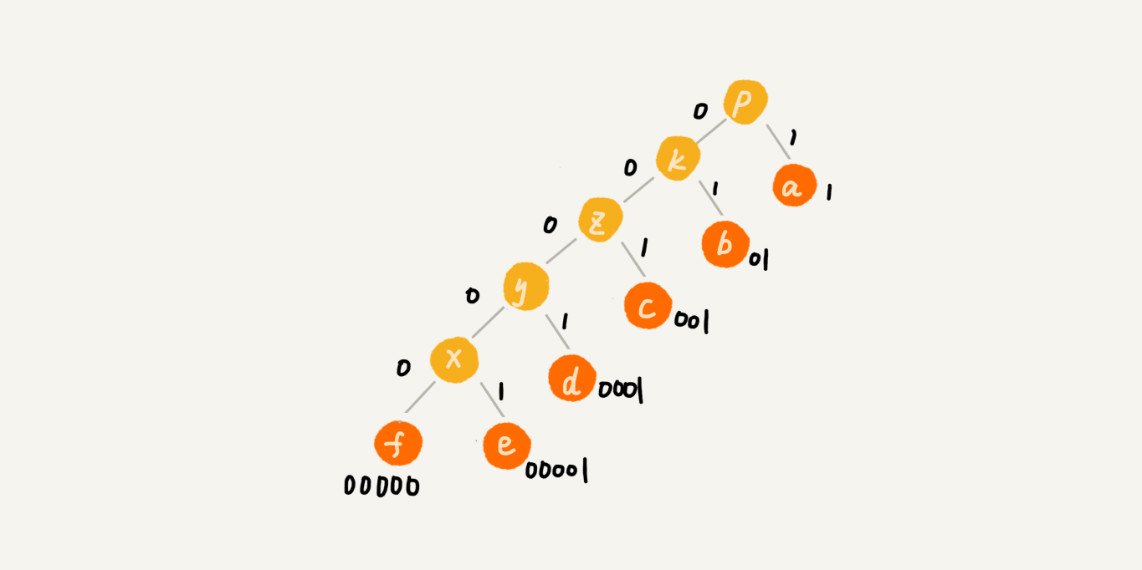
现在，我们给每一条边加上画一个权值，指向左子节点的边我们统统标记为 0，指向右子节点的边，我们统统标记为 1，那从根节点到叶节点的路径就是叶节点对应字符的霍夫曼编码。

ccf15d048be005924a409574dce143ed.jpg

接下来看一下编码实现：

  1. import java.util.ArrayList;
  2. import java.util.PriorityQueue;
  4. public class HuffmanTree {
  6.     public static class TreeNode<T> implements Comparable<TreeNode> {
  7.         E data;
  8.         int weight;
  9.         TreeNode left;
  10.         TreeNode right;
  12.         public TreeNode() {}
  13.         public TreeNode(E data, int weight) {
  14.             this(data, weight, null, null);
  15.         }
  16.         public TreeNode(E data, int weight, TreeNode left, TreeNode right) {
  17.             this.data = data;
  18.             this.weight = weight;
  19.             this.left = left;
  20.             this.right = right;
  21.         }
  22.         @Override
  23.         public String toString() {
  24.             return "TreeNode[data=" + data + ", weight=" + weight + "]";
  25.         }
  26.         @Override
  27.         public int compareTo(TreeNode t) {
  28.             return this.weight - t.weight;
  29.         }
  30.     }
  32.     public static void TreeNode createTree(ArrayList<TreeNode> list) {
  33.         PriorityQueue<TreeNode> pq = new PriorityQueue<>();
  34.         for (TreeNode node : list)
  35.             pq.add(node);
  36.         while(pq.size() > 1) {
  37.             TreeNode left = pq.poll();
  38.             TreeNode right = pq.poll();
  39.             // 构建新节点，节点的权重为左右子树相加的权重
  40.             TreeNode root = new TreeNode(null, left.weight + right.weight, left, right);
  41.             pq.add(root);
  42.         }
  44.         // 返回树的根节点
  45.         return pq.poll;
  46.     }
  48.     // 先序遍历
  49.     public static void preOrder(TreeNode root) {
  50.         if (root == null) return;
  51.         System.out.println(root);
  52.         preOrder(root.left);
  53.         preOrder(root.right);
  54.     }
  56.     // ... 省略后序、中序遍历
  58.     public static void main(String[] args) {
  59.         ArrayList<TreeNode> list = new ArrayList<>();
  60.         list.add(new TreeNode("A", 1));
  61.         list.add(new TreeNode("B", 1));
  62.         list.add(new TreeNode("C", 3));
  63.         list.add(new TreeNode("D", 4));
  64.         list.add(new TreeNode("E", 5));
  65.         list.add(new TreeNode("F", 6));
  66.         TreeNode root = createTree(list);
  67.         preOrder(root, 0);
  68.     }
  70. }

内容小结

今天我们学习了贪心算法。

实际上，贪心算法适用的场景比较有限。这种算法思想更多的是指导设计基础算法。比如最小生成树算法、单源最短路径算法，这些算法都用到了贪心算法。从我个人的学习经验来讲，不要刻意去记忆贪心算法的原理，多练习才是最有效的学习方法。

贪心算法的最难的一块是如何将要解决的问题抽象成贪心算法模型，只要这一步搞定之后，贪心算法的编码一般都很简单。贪心算法解决问题的正确性虽然很多时候都看起来是显而易见的，但是要严谨地证明算法能够得到最优解，并不是件容易的事。所以，很多时候，我们只需要多举几个例子，看一下贪心算法的解决方案是否真的能得到最优解就可以了。

课后思考

  1. 在一个非负整数 a 中，我们希望从中移除 k 个数字，让剩下的数字值最小，如何选择移除哪 k 个数字呢？
  2. 假设有 n 个人等待被服务，但是服务窗口只有一个，每个人需要被服务的时间长度是不同的，如何安排被服务的先后顺序，才能让这 n 个人总的等待时间最短？

答：

  1. 把原整数的所有数字从左到右进行比较，如果发现某一位数字大于它右面的数字，那么在删除该数字后，必然会使该数位的值降低，因为右面比它小的数字顶替了它的位置。具体实现看《漫画算法》。
  2. 每个人需要被服务的时间不一样，但所有人加起来总的被服务时间是固定的。题意是求n个人总的等待时间，每个人在被服务之前，所经过的等待时间是不同的。而当前被服务的人所需的服务时间，会累加到剩下的那些等待被服务人的等待时间上。
    所以要使n个人总的等待时间最短，那么每次安排服务时间最短的那个人被服务：堆排序（小顶堆）。

它山之石

找零问题不能用贪婪算法，即使有面值为一元的币值也不行：考虑币值为100，99 和 1 的币种，每种各一百张，找396元。
动态规划可求出四张99元，但贪心算法解出需三张一百和96张一元。