【实战】单调栈经典问题-柱状图中的最大矩形

这道题是 LeetCode 第84题，liweiwei题解暴力解法、栈（单调栈、哨兵技巧）

题意

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1。求在该柱状图中，能够勾勒出来的矩形的最大面积。

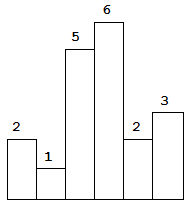
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为[2, 1, 5, 6, 2, 3]。

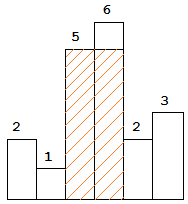
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

思路

首先，要想找到第 i 个位置最大面积是什么？这个其实才是这个问题最关键的点。

是以 i 为中心，向左找第一个小于 heights[i] 的位置 left_i；向右找第一个小于 heights[i] 的位置 right_i，

即最大面积为 heights[i] * (right_i - left_i - 1)，如下图所示：

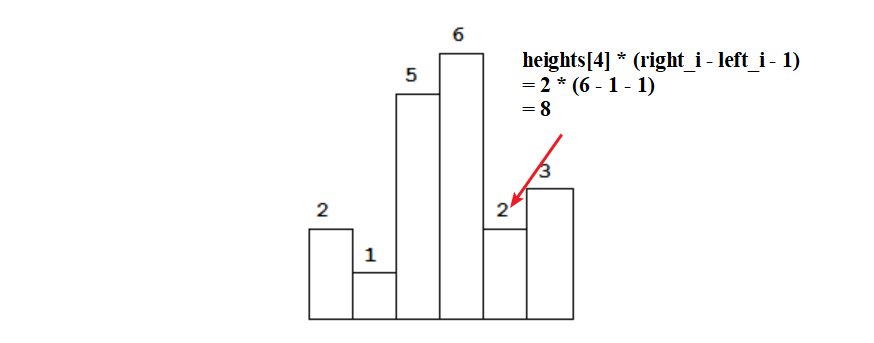
所以，我们的问题就变成如何找到 right_i 和 left_i？

1. 暴力解法

最简单的思路就是暴力解法（Brute Force），直接利用循环，当循环到 i 时，分别在 i 左右两边分别再接一次循环来寻找相应的值。

2. 动态规划

当我们找 i 左边第一个小于 hegihts[i] 如果 heights[i - 1] >= heights[i]，其实就是和求 heights[i - 1]左边第一个小于 heights[i - 1]一样。以此类推，右边同理。

3. 单调栈

其实上面动态规划的解法使用空间换时间，同样的单调栈也是利用栈来记录信息从而达到时间换空间的目的。

那记录什么信息呢？记录高度是不是可以呢？其实是不够的，因为计算矩形还需要计算宽度，很容易知道宽度是由下标确定的，记录了下标其实对应的高度就可以直接从输入数组中的得出，因此，应该记录的是下标。

代码

1. 暴力解法

public class Solution {
    public int largestRectangleArea(int[] heights) {
        int len = heights.length;
        int res = 0;
        for (int i = 0; i < len; i++) {
            int curHeight = heights[i];
            // 找左边最后 1 个大于等于 heights[i] 的下标
            int left = i;
            while (left > 0 && heights[left - 1] >= curHeight) {
                left--;
            }
            // 找右边最后 1 个大于等于 heights[i] 的下标
            int right = i;
            while (right < len - 1 && heights[right + 1] >= curHeight) {
                right++;
            }
            int width = right - left + 1;
            res = Math.max(res, width * curHeight);
        }
        return res;
    }
}

2. 动态规划

class Solution {
    public int largestRectangleArea(int[] heights) {
        if (heights == null || heights.length == 0) {
            return 0;
        }
        int n = heights.length;
        int[] left_i = new int[n];
        int[] right_i = new int[n];
        left_i[0] = -1;
        right_i[n - 1] = n;
        int res = 0;
        for (int i = 1; i < n; i++) {
            int temp = i - 1;
            while (temp >= 0 && heights[temp] >= heights[i]) {
                temp = left_i[temp];
            }
            left_i[i] = temp;
        }
        for (int i = n - 2; i >= 0; i--) {
            int temp = i + 1;
            while (temp < n && heights[temp] >= heighes[i]) {
                temp = right_i[temp];
            }
            right_i[i] = temp;
        }
        for (int i = 0; i < n; i--) {
               res = Math.max(res, (right_i[i] - left_i[i] - 1) * heights[i]);
        }
    }
}

3. 单调栈

class Solution {
    public int largestRectangleArea(int[] heights) {
        int len = heights.length, res = 0;
        Deque<Integer> stack = new ArrayDeque<>(len);
        for (int i = 0; i < len; i++) {
            // 这个 while 很关键，因为可能不止一个柱形的最大宽度可以被计算出来
            while (!stack.isEmpty() && heights[i] < heights[stack.peekLast()]) {
                int curHeight = heights[stack.pollLast()];
                while (!stack.isEmpty() && heights[stack.peekLast()] == curHeight) {
                    stack.pollLast();
                }
                int curWidth;
                if (stack.isEmpty()) {
                    curWidth = i;
                } else {
                    curWidth = i - stack.peekLast() - 1;
                }
                res = Math.max(res, curHeight * curWidth);
            }
            stack.addLast(i);
        }
        while (!stack.isEmpty()) {
            int curHeight = heights[stack.pollLast()];
            while (!stack.isEmpty() && heights[stack.peekLast()] == curHeight) {
                stack.pollLast();
            }
            int curWidth;
            if (stack.isEmpty()) {
                curWidth = len;
            } else {
                curWidth = len - stack.peekLast() - 1;
            }
            res = Math.max(res, curHeight * curWidth);
        }
        return res;
    }
}

以上代码需要考虑两种特殊的情况：

1. 弹栈的时候，栈为空；
2. 遍历完成以后，栈中还有元素；

为此我们可以在输入数组的两端加上两个高度为 0 （或者是 0.5，只要比 1 严格小都行）的柱形，可以回避上面这两种分类讨论。

这两个站在两边的柱形有一个很形象的名词，叫做哨兵（Sentinel）。

有了这两个柱形：

1. 左边的柱形（第一个柱形）由于它一定比输入数组里任何一个元素小，它肯定不会出栈，因此栈一定不为空；
2. 右边的柱形（最后的柱形）也正是因为它一定比输入数组里任何一个元素小，它会让所有输入数组里的元素出栈（第一个哨兵元素除外）。

这里栈对应到高度，呈单调增加不减的形态，因此称为单调栈（Monotone Stack）。它是暴力解法的优化，计算每个柱形的高度对应的最大矩形的顺序由出栈顺序决定。

下面是加入了哨兵的写法：

class Solution {
    public int largestRectangleArea(int[] heights) {
        int len = heights.length, res = 0;
        Deque<Integer> stack = new ArrayDeque<>();
        int[] new_heights = new int[len + 2];
        System.arraycopy(heights, 0, new_heights, 1, len);
        for (int i = 0; i < new_heights.length; i++) {
            while (!stack.isEmpty() && new_heights[stack.peek()] > new_heights[i]) {
                int cur = stack.pop();
                res = Math.max(res, (i - stack.peek() - 1) * new_heights[cur]);
            }
            stack.push(i);
        }
        return res;
    }
}