【实战】数组中的简单算法问题Ⅱ

简单的数组问题第二部分

题解报告LeetCode#56：合并区间

题意：LeetCode#56：合并区间

思路：

• 知识点：扫描线法
• 按照起点排序
• 类似问题：天际线问题

我们只关心最后添加进来的那个区间，因此需要用一个栈

代码：

class Solution {
    public int merge(int[][] intervals) {
        int len = intervals.length;
        if (len == 0) {
            return new int[0][0];
        }
        //按照起点排序
        Arrays.sort(intervals, Comparator.comparingInt(i -> i[0]));
        Stack<int[]> stack = new Stack<>();
        for (int i = 1; i < len; i++) {
            if (stack.peek()[1] < intervals[i][0]) {
                stack.push(intervals[i]);
            } else {
                //更新
                stack.peek()[1] = Math.max(stack.peek()[1], intervals[i][1]);
            }
        }
        return stack.toArray(new int[0][]);
    }
}

题解报告LeetCode#215：数组中的最大元素

题意：LeetCode#215：数组中的最大元素

在未排序的数组中找到第 **k** 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

思路：

• 方法一：暴力解法；
• 方法二：借助 partition 操作定位到最终排定以后索引为 len - k 的那个元素（特别注意：随机化切分元素）> 注意事项：

  快速排序虽然快，但是如果实现得不好，在遇到特殊测试用例的时候，时间复杂度会变得很高。如果你使用partition的方法完成这道题，时间排名不太理想，可以考虑一下是什么问题，这个问题很常见。

以下的描述基于”快速排序“算法知识的学习，可以复习一下 partition 过程、分治思想和“快速排序”算法的优化。
分析：我们在学习“快速排序”的时候，接触的第一个操作就是 partition ，简单介绍如下：

• 对于某个索引 j，nums[j]已经排定，即nums[j]经过 partition （切分）操作以后会放置在它“最终应该放置的地方”；
• nums[left] 到 nums[j - 1] 中的所有元素都不大于 nums[j]；
• nums[j + 1] 到 nums[right] 中的所有元素都不小于 nums[j]。

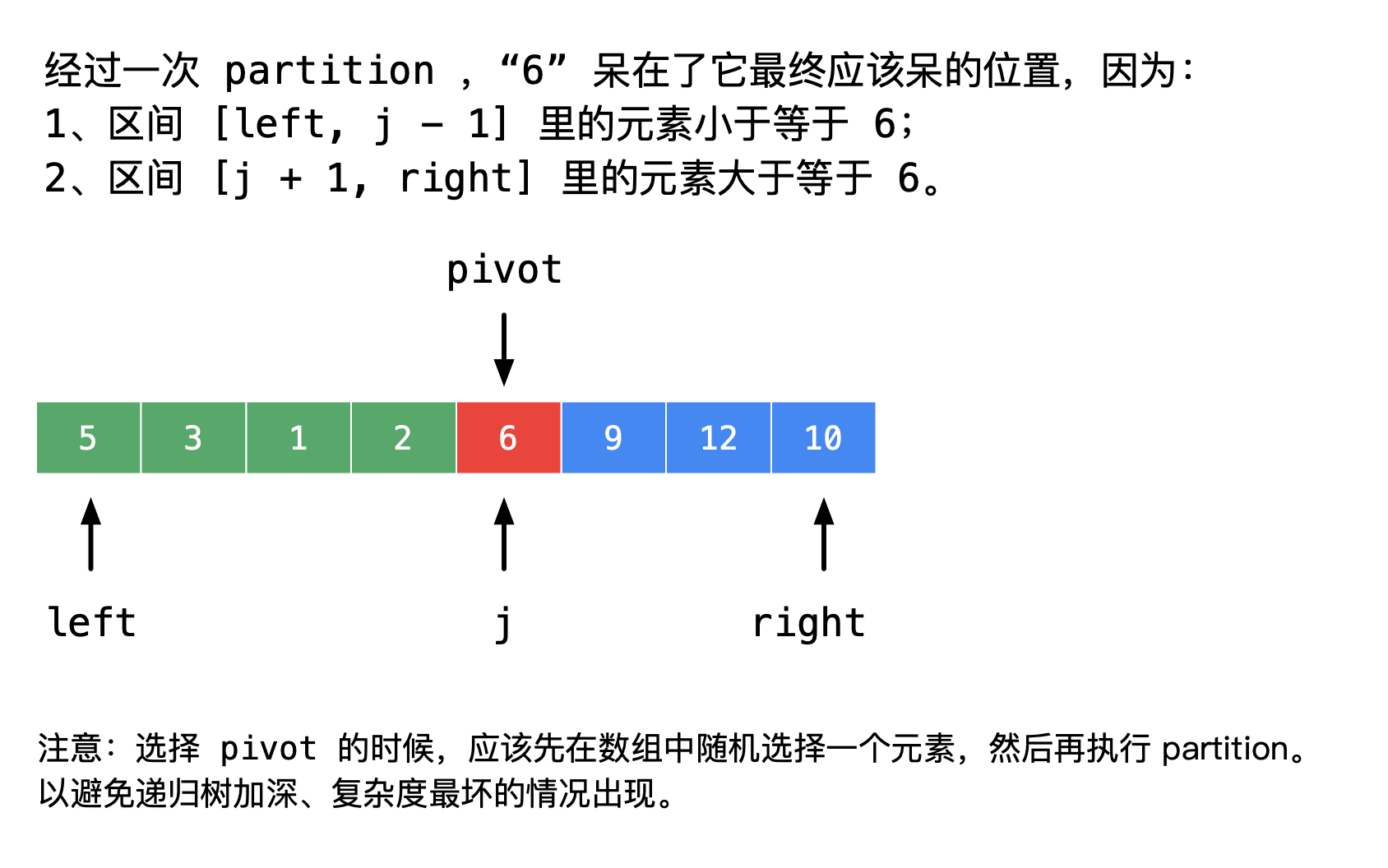
partition（切分）操作总能排定一个元素，还能够知道这个元素它最终所在的位置，这样每经过一次 partition（切分）操作就能缩小搜索的范围，这样的思想叫做 “减而治之”（是 “分而治之” 思想的特例）。
代码：
方法一：

public class Solution {
    public int findKthLargest(int[] nums, int k) {
        int len = nums.length;
        Arrays.sort(nums);
        return nums[len - k];
    }
}

方法二：

public class Solution {

    pubic int findKthLargets(int[] nums, int k) {
        int len = nums.length;
        int left = 0;
        int right = len - 1;

        //转换一下，第k大元素的索引是 len - k
        int target = len - k;

        while (true) {
            int index = partition(nums, left, right);
            if (index == target) {
                return nums[index];
            } else if (index < target) {
                left = index + 1;
            } else {
                right = index - 1;
            }
        }
    }

    public int partition(int[] nums, int left, int right) {
        int pivot = nums[left];
        int j = left;
        for (int i = left + 1; i <= right; i++) {
            if (nums[i] < pivot) {
                // 小于 pivot 的元素都被交换到前面
                j++; // 这里要记住是先 j++ 再去做交换
                swap(nums, j, i);
            }
        }
        // 在之前遍历的过程中，满足 [left + 1, j] < pivot，并且 (j, i] >= pivot
        swap(nums, j, left);
        // 交换以后 [left, j - 1] < pivot, nums[j] = pivot, [j + 1, right] >= pivot
        return j;
    }

    private void swap(int[] nums, int index1, int index2) {
        int temp = nums[index1];
        nums[index] = nums[index2];
        nums[index2] = temp;
    }

}