题解报告LeetCode#4：寻找两个有序数组的中位数

题意：LeetCode#4：寻找两个有序数组的中位数；他山之玉：liweiwei1419

思路：“使用二分查找找到两个数组的边界线”

中位数：在有两个有序数组的时候，仍然可以把两个数组分割成两个部分。

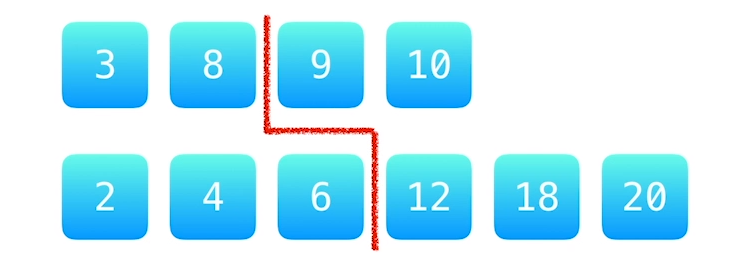
image-20200921231653645.png

我们使用一条分割线把两个数组分别分割成两部分：

  1. 红线左边和右边的元素个数相等，或者左边元素的个数比右边元素的个数多 1 个；
  2. 红线左边的所有元素的数值 <= 红线右边的所有元素的数值；

那么中位数就一定只与红线两侧的元素有关，确定这条红线的位置使用二分查找。

代码：

  1. public class Solution {
  3.     public double findMedianSortedArrays(int[] nums1, int[] nums2) {
  4.         // 为了让搜索的范围更小，我们始终让 nums1 是那个更短的数组
  5.         if (nums1.length > nums2.length) {
  6.             int[] temp = nums1;
  7.             nums1 = nums2;
  8.             nums2 = temp;
  9.         }
  11.         int m = nums1.length;
  12.         int n = nums2.length;
  14.         // 分割线左边的所有元素需要满足的个数 m + (n - m + 1) / 2;
  15.         int totalLeft = (m + n + 1) / 2;
  17.         // 在 nums1 的区间 [0, m] 里查找恰当的分割线
  18.         // 使得 nums1[i - 1] <= nums2[j] && nums2[j - 1] <= nums1[i]
  19.         int left = 0;
  20.         int right = m;
  22.         while (left < right) {
  23.             int i = left + (right - left + 1) / 2;
  24.             int j = totalLeft - i;
  25.             if (nums1[i - 1] > nums2[j]) {
  26.                 // 下一轮的搜索区间 [left, i - 1]
  27.                 right = i - 1;
  28.             } else {
  29.                 // 下一轮的搜索区间 [i, right]
  30.                 left = i;
  31.             }
  32.         }
  34.         int i = left;
  35.         int j = totalLeft - i;
  36.         int nums1LeftMax = i == 0 ? Integer.MIN_VALUE : nums1[i - 1];
  37.         int nums1RightMin = i == m ? Integer.MAX_VALUE : nums1[i];
  38.         int nums2LeftMax = j == 0 ? Integer.MIN_VALUE : nums2[j - 1];
  39.         int nums2RightMin = j == n ? Integer.MAX_VALUE : nums2[j];
  41.         if (((m + n) % 2) == 1) {
  42.             return Math.max(nums1LeftMax, nums2LeftMax);
  43.         } else {
  44.             return (double) ((Math.max(nums1LeftMax, nums2LeftMax)) +
  45.                              (Math.min(nums1RightMin, nums2RightMin))) / 2;
  46.         }
  47.     }
  49. }