《算法导论》第 21 章：用于不相交集合的数据结构

《数据结构与算法分析-Java语言描述》第 8 章：不相交类

  • [并查集] 是一种建立在 [数组] 上的树形结构，并且这棵树的特点是孩子结点指向父亲结点；
  • [并查集] 主要用于解决 [动态连通性] 问题，重点关注的是连接问题，并不关注路径问题；
  • [并查集] 是树，所以优化的策略依然是和树的高度较劲，优化思路有 [按秩合并] 与 [路径压缩]。

image-20201013202254328.png

一、what is the Disjoint-set

并查集（Union Find）也称不相交集合（Disjoint-set）。它用以维护一个不相交动态集的集合 S = {S1, S2, …, Sk}。我们用一个代表（representative）来标识每个集合，它是这个集合的某个成员。在一些应用中，我们不关心哪个成员被用来作为代表，仅仅关心的是 2 次查询动态集合的代表中，如果这些查询没有修改动态集合，则这两次查询应该得到相同的答案。其他一些应用可能会需要一个预先说明的规则来选择代表，比如选择这个集合中最小的成员（当然假设集合中的元素能被比较）。这里要是看不懂就直接往后看吧，这种数据结构比较抽象，但是实际实现起来又十分简单。

1. union and find

并查集主要提供了以下两个操作，分别就是并查集这个名字中的前两个字：

  • 并：就是将两个集合合并在一起，表示这两个集合之间产生连接；
  • 查：查询元素属于哪个集合，但我们更经常用于查询两个元素是不是连接在一起；

2. 函数实现

我们需要用一个对象表示一个集合的每个元素。设 x 表示一个对象，那么并查集的实现需要支持以下三个操作：

  • MAKE-SET(x)：建立一个新的集合，它的唯一元素只有 x 所代表的对象所属的类。
  • UNION(x, y)：将包含 x 和 y 的两个动态集合（表示为 Sx 和 Sy）合并成一个新的集合，即这两个集合的并集。
  • FIND_SET(x)：返回一个指向包含 x 的（唯一）集合的代表。

这么说还是太抽象了，下面以一个简单 Demo 来距离，假设现在有 0~7 之间八个节点，如下所示：

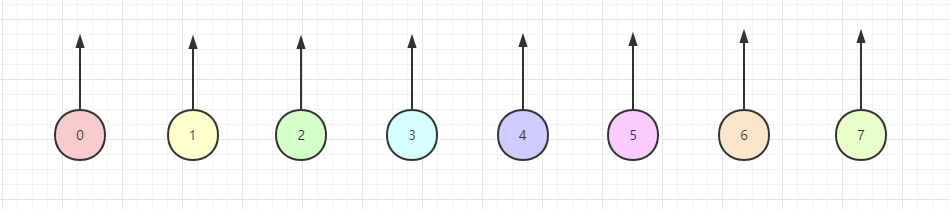
image-20201013212416516.png

为了执行两个集合的 union 运算，我们通过使一颗树的根的父链链接到另一棵树的根节点来合并两棵树。显然，这种操作花费常数时间。接下来的三张图分别表示在 union(4, 5) 、 union(6, 7)、 union(4, 6) 三次操作后所显示的森林（没错，树的集合叫做森林）。

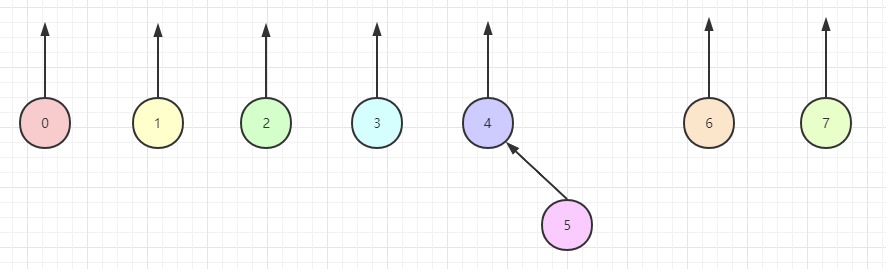
image-20201013212919886.png

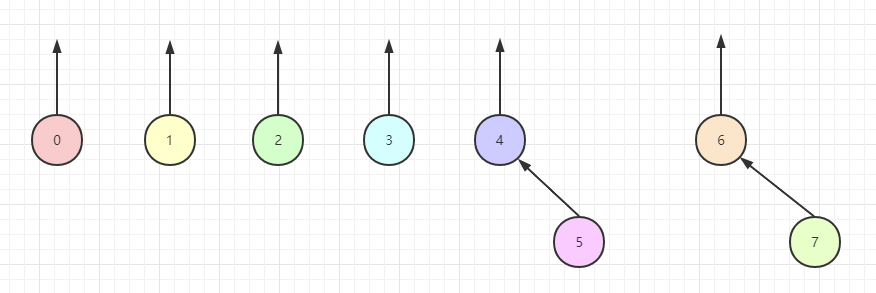
image-20201013212958994.png

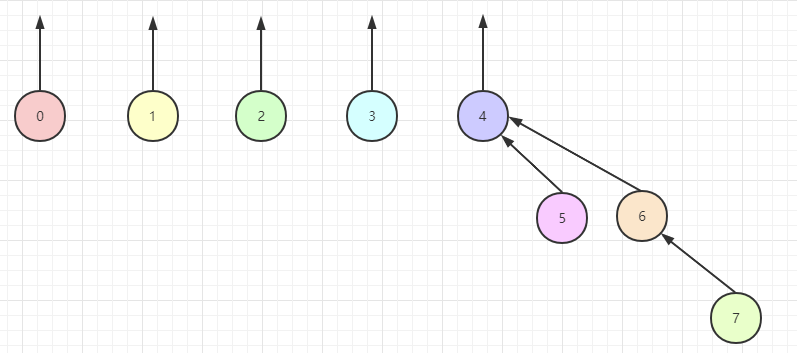
image-20201013213032495.png

我们上面提到过，并查集一般都是用数组来表示的，接下来我们看下在上面三步操作后，并查集的数组中元素的值：

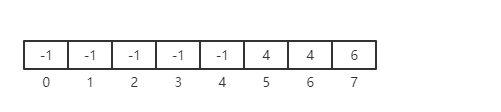
image-20201013213558102.png

那么，此时我们再调用 findSet(5, 6)，我们就可以判断出 5和6 都在同一颗树上，调用 findSet(5, 7) 也是可以的，看你代码如何实现咯，我们可以先看到 7 的对应的值为 6，那么我们应该再去找 6，6对应的值为 4，那么就和 5 相同了。

3. 并查集与路径问题

并查集主要用于解决联通问题，即抽象概念中结点和结点间是否连接。

路径问题，不仅仅要考虑联通问题，我们往往还要求出最短路径，这并不是并查集做的事情。因此并查集问题能做的事情比路径问题少，它更专注于：

  • 判断连接状态（查）；
  • 改变连接状态（并）。

通常我们刷题所需要的代码会要求实现以下 3 个功能：

  1. find(p)：查找元素 p 所对应的集合，这个函数有些时候仅作为私有函数被下面两个函数调用。
  2. union(p, q)：合并元素 p 和 元素 q 所在的集合。
  3. isConnection(p, q)：查询元素 p 和元素 q 是不是在同一集合中。

因此，我们要实现的并查集其实就是要实现下面的这个接口：

  1. public interface IUnionFind {
  3.     // 并查集的版本名称，由开发者指定
  4.     String versionName();
  6.     // p (0 到 N-1)所在的分量的标识符
  7.     int find(int p);
  9.     // 如果 p 和 q 存在于同一分量中则返回 true
  10.     boolean isConnected(int p, int q);
  12.     // 在 p 与 q 之间添加一条连接
  13.     void union(int p, int q);
  15. }

二、并查集的实现

1. 并查集第一版（quick-find实现）

1.1 思路过程

这一版本实现的最基本思路就是：给每个元素改名字，名字一样，就表示在同一集合中。

  • 优点：查询两个元素是否在一个集合中很快；
  • 缺点：把两个集合合并为一个集合效率很低。

这一版本[并查集]并不常用，仅作为了解。

并查集可以使用数据表示。这个数组我们命令为 id。初始化的时候每一个元素的值都是不一样的。如果值一样的，表示是属于同一集合内的元素。

基于 id 的 quick-find 的思路：设置 id 数组，数组的每个元素是分量标识。

从 quick-find 这个名字上看，我们这一版的实现，对于 find(int p) 这个操作来说是高效的，但对于 union(int p, int q) 这个操作是低效的，因为需要遍历整个并查集。find(int p) 这个操作的时间复杂度是 O(1), 而 union(int p, int q) 这个操作的时间复杂度是 O(n)，要全部遍历并查集中的元素，把其中一个分量标识的所有结点的编号更改为另一个一个分量标识。

1592162475356-e3733488-2455-4763-9ff6-9eca8b0678ea.png

例如上面的表格中，如果我们要将第 1 行的 0 和 1 执行 union(int p, int q) 操作，有两种方式：

  • 第 1 种方式：把第 1 行的 0，2，4，6，8 的值全改成 1；
  • 第 2 种方式：把第 1 行的 1，3，5，7，9 的值全改成 0。

可以看到，union(int p, int q) 的操作和问题的规模成正比，所以 quick-find 思想（基于 id）的 union(int p, int q) 操作时间复杂度是 【理论】并查集知识入门 - 图8。

1.2 代码实现

public class UnionFind1 implements IUnionFind {

    private int[] id; // 分量 id
    private int count; // 连通分量的数量

    public UnionFind1(int n) {
        this.count = n;
        id = new int[n];
        for (int i = 0; i < n; i++) {
            id[i] = i;
        }
    }

    @Override
    public String versionName() {
        return "并查集的第 1 个版本，基于 id 数组，quick-find";
    }

    // 以常数时间复杂度，返回分量的标识符，与并查集的规模是无关的，这一步很快
    // 因此我们称这个版本的并查集是 quick-find
    @Override
    public int find(int p) {
        return id[p];
    }

    @Override
    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }

    // 因为需要遍历数组中的全部元素，所以这个版本其实效率并不高
    @Override
    public void union(int p, int q) {
        int pid = find(p);
        int qid = find(q);

        // 如果 p 和 q 已经在相同的分量之中，则什么都不做
        if (pid == qid) {
            return;
        }

        // 将 p 的分量重新命名为 q 的名称
        for (int i = 0; i < id.length; i++) {
            if (find(i) == pid) {
                id[i] = qid;
            }
        }
        // 每次 union 以后，连通分量减 1
        count--;
    }
}

2. 并查集第二版（quick-union实现）

1. 思路过程

我们不再使用 id 数组，而使用 parent 数组，parent 数组的定义是：parent[i] 表示索引为 i 的结点的父亲结点的索引，在这个定义下，根节点的父亲结点是自己。

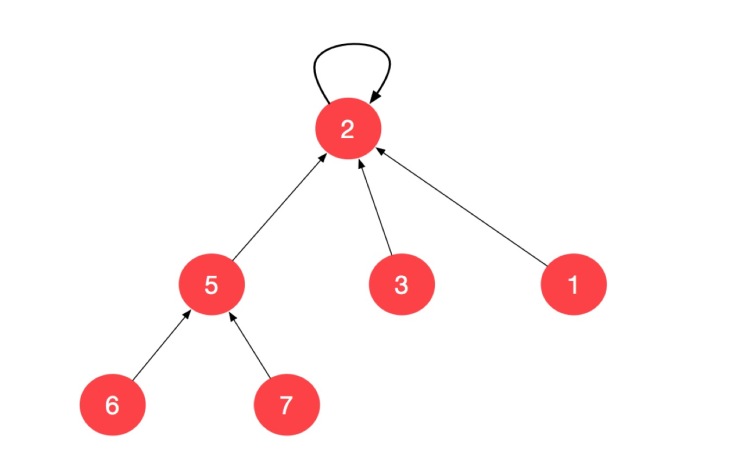
1592159429484-f403794f-ad72-4d1b-9ef0-486e829b3215.jpeg

此时查询结点 p 和结点 q 相连这件事情，就是我们分别追溯 parent[p] 和 parent[q] （可以看到这样的过程很像在一棵树上进行操作），查询到 parent[p] 和 parent[q] 根结点相同，那么它们就同属于一个集合。

这样看来，find(int p)好像费点劲，这也是我们接下来的几个并查集优化的方向，都是在 find(int p) 上做文章，但这保证了 union(int p, int q) 很快，我们只需要把其中一个结点的父结点指向另一个结点的根节点（而谁的父结点指向谁的根节点，也就是我们后几版并查集优化的方向），就完成了 union(int p, int q) 的操作。此时 union(int p, int q) 的操作只需要一行代码：

parent[pRoot] = qRoot;

初始化的时候，我们将每个元素都指向自己，此时表示这 10 个结点互相之间没有连接关系。如下表所示：

1592159429491-6dda3117-3758-47f6-b4f3-a7661d261ca7.jpeg

上面的数组表示的并查集如下：

1592159429459-a85ca92f-50c7-439d-98cd-e0a4343bea74.jpeg

2. 代码实现

public class UnionFind2 implements IUnionFind {

    private int[] parent; // 第 i 个元素存放它的父元素的索引
    private int count; // 连通分量的数量

    public UnionFind2(int n) {
        this.count = n;
        parent = new int[26];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }

    @Override
    public String versionName() {
        return "并查集的第 2 个版本，基于 parent 数组，quick-union";
    }

    @Override
    public int find(int p) {
        // 跟随链接找到根结点
        while (parent[p] != p) { // 只要不是根结点
            p = parent[p];
        }
        return p;
    }

     @Override
    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }

    @Override
    public void union(int p, int q) {
        int pRoot = find(p); // 将 p 归并与之相同的分量中
        int qRoot = find(q); // 将 q 归并与之相同的分量中

        // 如果 p 和 q 已经在相同的分量之中，则什么都不做
        if (pRoot == qRoot) {
            return;
        }
        // 如果 parent[qRoot] = pRoot; 也是可以的，即将其中一个结点指向另一个结点
        parent[pRoot] = qRoot;
        // 每次 union 以后，连通分量减 1
        count--;
    }

}

三、并查集的优化

1. 并查集第三版（quick-union）基于 size 的优化

1.1 思路过程

这一版本[并查集]代码是最基本的[并查集]，我们需要学习思想，核心思想是[代表元法]，以[树]的[根节点]作为代表元。

后续介绍这一版本的两个优化：

  1. 按秩合并（有两个版本）
  2. 路径压缩（有两个版本）

介绍得多，只是为了方便大家建立知识结构，真正我们只会使用一个版本的「并查集」。我们放在介绍完了以后再说。

我们发现 union(4, 9) 与 union(9, 4) 其实是一样的，也就是把谁的根指向谁的根，这一点从正确性上来说是无关紧要的，但是对于 find 的时间复杂度就会有影响。为此，我们做如下优化。

在合并之前做判断，具体做法是，计算每一个结点有多少个元素直接或者间接地以它为根，我们应该将集合元素少的那结点的根指向集合元素多的那个结点的根。这样，形成的树就会更高效率地形成一颗层数较低的树。

为此，我们再引入一个 size 数组，size[i] 的定义是：以第 i 个结点为根的集合的元素的个数。

在初始化的时候 size[i] == 1，find 和 isConnected操作中我们都不必去维护 size 这个数组，唯独在 unionElements 的时候，我们才要维护 size 数组的定义。

1.2 代码实现

public class UnionFind3 implements IUnionFind {

    private int[] parent; // 第 i 个元素存放它的父元素的索引

    private int count; // 连通分量的数量

    private int[] size; // 以当前索引为根的树所包含的元素的总数

    public UnionFind3(int n) {
        this.count = n;
        parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            size[i] = 1;
        }
    }

     @Override
    public String versionName() {
        return "并查集的第 3 个版本，基于 parent 数组，quick-union，基于 size";
    }

    // 返回索引为 p 的元素的根结点的索引
    @Override
    public int find(int p) {
        // 跟随链接找到根结点
        while (p != parent[p]) {
            p = parent[p];
        }
        return p;
    }

    @Override
    public boolean isConnected(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        return pRoot == qRoot;
    }

    @Override
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot == qRoot) {
            return;
        }
        // 这一步是与第 2 版不同的地方，我们不是没有根据地把一个结点的根结点的父结点指向另一个结点的根结点
        // 而是将小树的根结点连接到大树的根结点
        if (size[pRoot] > size[qRoot]) {
            parent[qRoot] = pRoot;
            size[pRoot] += size[qRoot];
        } else {
            parent[pRoot] = qRoot;
            size[qRoot] += size[pRoot];
        }
        // 每次 union 以后，连通分量减 1
        count--;
    }

}

2. 并查集第四版（quick-union）基于 rank 的优化

2.1 思路过程

基于 rank 的优化是使用得更多，因为这样做更合理一些。 但是维护数组 rank 的定义是相对麻烦的，通常的做法就是不维护，只是把数组 rank 作为两个集合合并的参考，即使是错的，也比随机合并的结果好。

使用 size 来决定将哪个结点的根指向另一个结点的根，其实并不太合理，但并不能说不正确，因为谁的根指向谁的根，其实都没有错，下面就是一个特殊的情况。

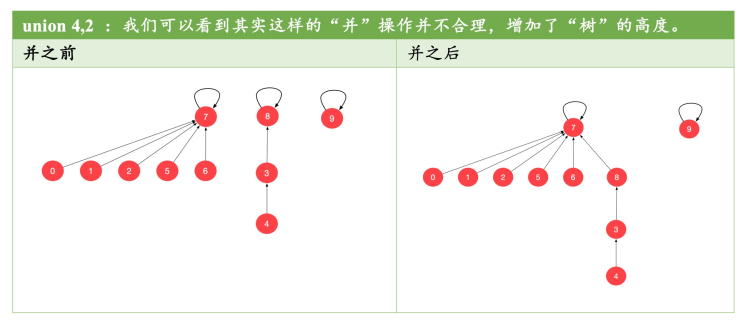
1592160242607-04a0424e-caa8-4645-b63c-9e4ebf6061fa.png

因为我们总是期望这棵树的高度比较低，在这种情况下，我们在 find 的时候，就通过很少的步数来找到根节点，进而提高 find 的效率。为此，我们引入 rank 数组，其定义是：rank[i] 表示以第 i 个元素为根的树的高度。

2.2 代码实现

public class UnionFind4 implements IUnionFind {

    private int[] parent;

    private int count;

    // 以下标为 i 的元素为根结点的树的深度（最深的那个深度）
    private int[] rank;

    public UnionFind4(int n) {
        this.count = n;
        parent = new int[n];
        rank = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            // 初始化时，所有的元素只包含它自己，只有一个元素，所以 rank[i] = 1
            rank[i] = 1;
        }
    }

    @Override
    public String versionName() {
        return "并查集的第 4 个版本，基于 parent 数组，quick-union，基于 rank";
    }

    // 返回下标为 p 的元素的根结点
    @Override
    public int find(int p) {
        while (p != parent[p]) {
            p = parent[p];
        }
        return p;
    }

    @Override
    public boolean isConnected(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        return pRoot == qRoot;
    }


    @Override
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot == qRoot) {
            return;
        }
        // 这一步是与第 3 版不同的地方
        if (rank[pRoot] > rank[qRoot]) {
            parent[qRoot] = pRoot;
        } else if (rank[pRoot] < rank[qRoot]) {
            parent[pRoot] = qRoot;
        } else {
            parent[qRoot] = pRoot;
            rank[pRoot]++;
        }
        // 每次 union 以后，连通分量减 1
        count--;
    }
}

3. 并查集第五版（quick-union）基于路径压缩的非递归实现

3.1 思路过程

这一版本代码用得最多。因为好理解，且代码量较少。

只用理解这一句即可 parent[p] = parent[parent[p]];，可以称之为「隔代压缩」。

虽然压缩不彻底，但是多压缩几次也就能够达到完全压缩的效果，且不使用递归，占用「递归栈」空间。

什么是路径压缩 path Compression？以上我们都是针对于 union 操作的优化，其实我们在 find 的时候，就可以对一棵树进行整理，让它的高度变低，这一点是基于并查集的一个特性：只要它们是连在一起的，其实谁指向谁，并不重要，所以我们在接下来的讨论中看到的并查集的表示图，它们是等价的，即它们表示的都是同一个并查集。

路径压缩 path Compression 的思路：在 find 的时候一次又一次的整理，将并查集构造（整理）成一个与之等价的并查集，使得后续的每一次 find 这样的操作路径最短。

假设一个最极端的并查集的图表示如下：

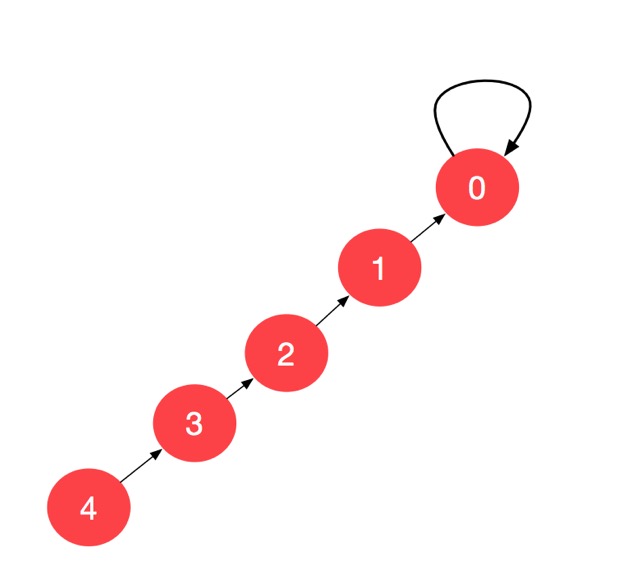
1592160458473-b531cb6a-4edd-4d38-a316-e20e7f7d4147.jpg

我们开始找 4 的父亲结点，4 的父亲结点不是 4 ，说明不是根结点，此时，我们尝试 2 步一跳，将 4 的父亲结点改成 4 的父亲结点的父亲结点，于是得到一个等价的并查集：

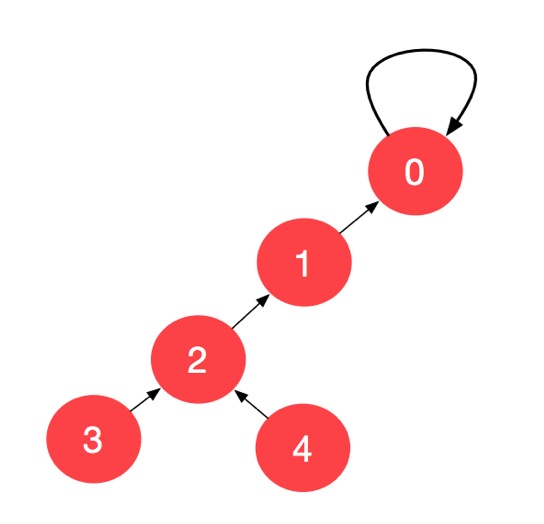
1592160458501-6cfcf23c-afdb-46f7-8791-e8fab38f0056.jpg

下面我们该考察元素 2 了，2 的父亲结点是 1，2 不是根结点，所以我们继续两步一跳，把 2 的父亲结点设置成它的父亲结点的父亲结点，于是又得到一个等价的并查集：

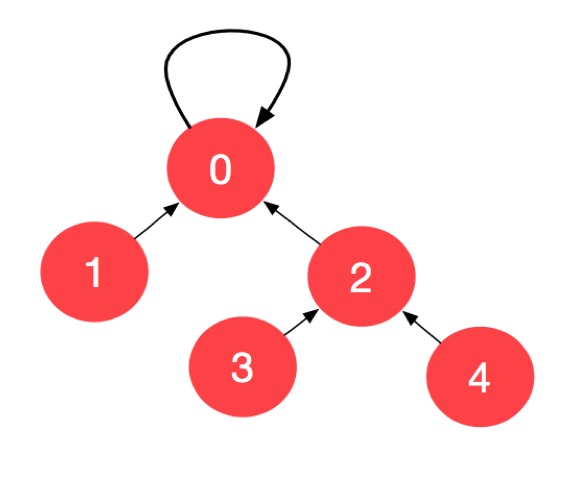
1592160458500-dce8e037-0f69-4d01-bae6-d6f374523004.jpg

此时，整棵树的高度就在一次 find 的过程中被压缩了。这里有一个疑问：即使我们在最后只差一步的情况下，我们跳两步，也不会出现无效的索引。其实，一步一跳，两步一跳，甚至三步一跳都没有关系。

画图画了这么多，代码实现只有一行：parent[p] = parent[parent[p]]; 编写的时候要注意这行代码添加的位置，画一个示意图，想想这个路径压缩的过程，就不难写出。

3.2 代码实现

public int find(int p) {
    // 在 find 的时候执行路径压缩
    while (p != parent[p]) {
        // 编写这句代码的时候可能会觉得有点绕，
        // 画一个示意图，就能很直观地写出正确的逻辑
        // 两步一跳完成路径压缩
        parent[p] = parent[parent[p]];
        p = parent[p];
    }
    return p;
}

根据上面的图，我们通过 find 操作执行路径压缩，最终形成的并查集如下：

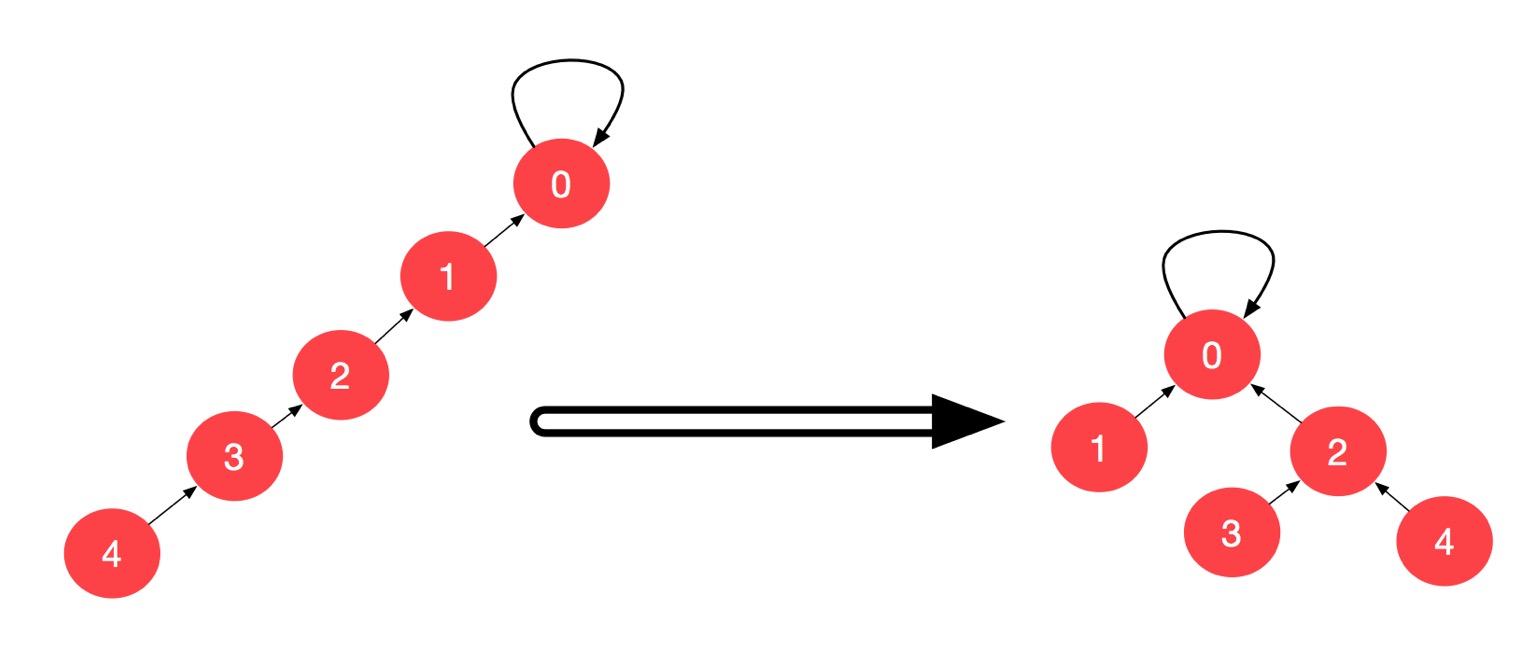
1592160458509-afc82200-84a9-45e7-b649-ce4c50a8a42d.jpg

4. 并查集第六版（quick-union）基于路径压缩的递归实现

4.1 思路过程

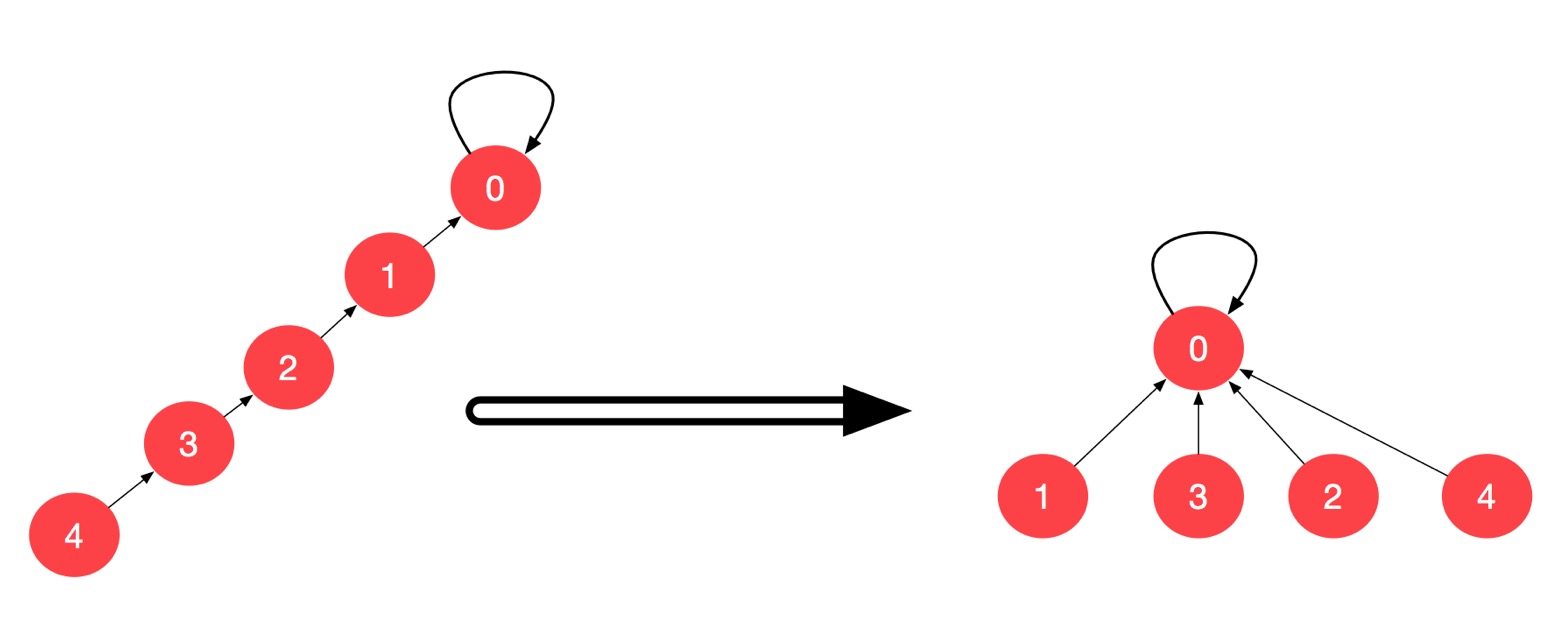
代码的实现的理解有一些绕。这一版我们实现压缩更彻底的路径压缩。其实我们不看上面的分析，我们想象路径压缩的目的是什么，就是让我们的并查集表示的树结构层数更低，那么最优的情况应该是下面这样，把一棵树压缩成 2 层，所有的结点都指向一个根，这才是把一个并查集压缩到最彻底的情况。

【理论】并查集知识入门 - 图17

那么，代码又应该如何实现呢？我们需要使用递归的思想。这一版代码的实现难点就在于：应该定义 find(p) 返回的是 p 这个结点的父结点。

4.2 代码实现

public int find(int p) {
    // 注意：这里是 if 不是 while，否则就变成循环
    if (p != parent[p]) {
        // 这一行代码的逻辑要想想清楚
        // 只要不是根结点
        // 就把父亲结点指向父亲结点的父亲结点
        parent[p] = find(parent[p]);
    }
    return parent[p];
}

最后，我们来比较一下基于路径压缩的两种方法。

1592161013465-6fda1d4e-56fc-4d0d-a40c-35db3bfd56a4.jpg

并查集能够很好地帮助我们解决网络中两个结点是否连接的问题。但是，对于网络中的两个结点的路径，最短路径的问题，我们就要使用图来解决。

5. 关于路径压缩的思考

写到这里，我们发现在路径压缩的过程中，我们之前引入的辅助合并的数组，不管是 rank 还是 size，它们的定义都不准确了，因为我们在路径压缩的过程中没有对它们的定义进行维护。这一点其实并不影响我们的算法的正确性，我们不去维护 rank 数组和 size 数组的定义，是因为第 1 点：难于实现，第 2 点： rank 数组还是 size 数组的当前实现仍然可以作为一个参考值，比起随机的做法要更有意义一些。

其实写到这里，数组 rank 还是数组 size 的意义都不太重要了，我们只须要在 find 的时候，做好路径压缩，把孩子结点指向父亲结点即可。