这章感觉老师讲得很仓促，作业也很随便，就挑一个我觉得会考的复习一下吧

最大网络流

image.png

人工解决

我们把源点、汇点和边的代号给编辑一下
image.png
从S汇出的流能走几条路？

  • a-d
  • b-c-d
  • b-e-f

三条，这三条路中的流量是多少？

  • a-d：8，因为a是8限制了流
  • b-c-d：3，但是除了因为c限制了3的流量之外，还有另一件事需要注意。因为a-d这条路占用了d中的8个容量，所以在进行b-c-d计算的时候要记住，3的由来是min(10,3,4).
  • b-e-f：3，因为min(7,3,5)

于是，总的流量加起来是8+3+3 = 14
看起来还是挺好弄得吗，似乎只要遍历每条路，然后便利的时候每条边取最小值然后减去最小值就行了。
OK，换了例子。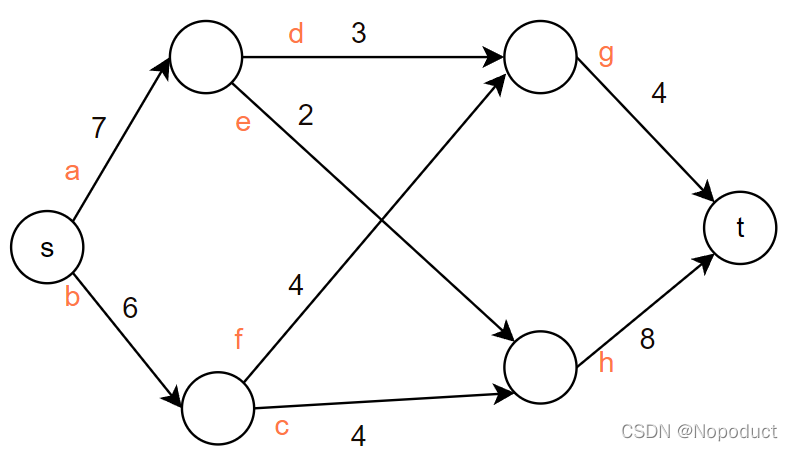
image.png
先求得该图得最大流

  • a-d-g：3
  • a-e-h：2
  • b-f-g：1 = min(6,4,1)
  • b-c-h：4 = min(5,4,6)

最大流为10。
接下来我们将引出计算机得缺陷了——他不懂顺序得重要性。我们首先遍历从a边出去的流，得到的答案没什么问题，但是计算机不知道，我们完全无法得知他会先计算那条边，假设我们先从b边开始

b-f-g：4
b-c-h：2 = min(2,4,8)
a-d-g：0 = min(7,3,0)
a-e-h：2 = min(7,2,6)
最终，我们得出图的最大流为8。
这就是计算机的问题所在，我们需要招到一种方法（算法），让计算机能够不在乎先后完美的计算出正确的答案。

问题分析

我们不妨分析分析为什么顺序会影响结果。
当我们率先计算b-f-g这条边的时候，我们贪心的把整条路都填满，导致g的容量全部被来自b的量占据了。这代表着a无法再利用这条边，只能向下从e流出。
甚至我们可以想象，在复杂的网络中，一个节点的流出的边很可能全部被其他流占用，导致流向该节点的“货物”全部失效了。如果这部分货物占据了总流量的很大部分，那么结果就很有可能出现错误。
为了避免这个现象Ford-Fulkerson算法建立了反向边，即“反悔”机制。
它，是这样做的。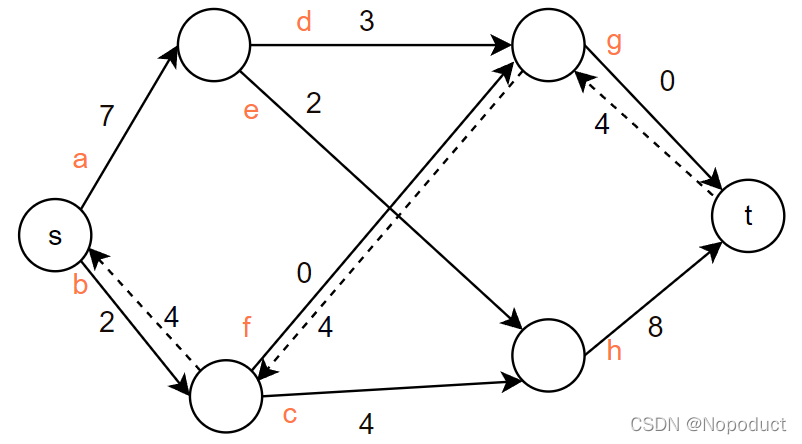
image.png
算法沿着路径反向建立额外的路，这条额外的路的容量就等于整条路的流量。
此时，我们完成了第一步，即b-f-g：4
然后我们继续

  • b-c-h：2
  • a-d-f’-c-h：2
  • a-e-h：2

最大流4+2+2+2=10。结果正确。
在这里你能看到“反悔”机制是如何作用的，他将多余的流量回退。本来正确的路线是b-f-g：1（一开始人工分配的最大流），结果我们因为顺序的不同导致b-f-g率先占据更多的容量，而反向边的建立使得我们有机会将多余的3份流量回退回去，产生正确的结果。