分支限界法类似回溯，但回溯法的求解目标是找出解空间中满足约束条件的所有解，而分支限界法的目标是找出满足约束条件的一个解，或是在满足约束条件的解中找出使某一目标函数值达到极大或极小的解即在某种原因上的最优解。回溯法以深度优先的方式搜索解空间树，而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间树。
基本过程：在分支限界法中，每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点，就一次性产生其所有儿子结点。在这些儿子结点中，导致不可行解或导致非最优解的儿子结点被舍弃，其余儿子结点被加入活结点表中。此后，从活结点表中取下一结点成为当前扩展结点，并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止。

例题1

题目

有一个由数字 0、1 组成的方阵中，存在一任意形状的封闭区域，封闭区域由数字1 包围构成，每个节点只能走上下左右 4 个方向。现要求只把【最大封闭区域】内的空间填写成2 。
例如： 6×6 的方阵：
6
0 1 0 0 0 0
1 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1

填写后如下：
0 1 0 0 0 0
1 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1

思路分析

1）首先确定一个合理的限界函数，根据该函数确定目标函数的界：
dx >= 0 && dx <= n + 1 && dy >= 0 && dy <= n + 1 && a[dx][dy] == 0
2）按照广度优先搜索策略搜索，在分支结点上依次扩展该结点的子结点，分别估算子结点的目标函数可能性，如果满足条件则压入队列，当某一位置的所有可能都被搜索，弹出该位置，重复以上过程。
3）先找出所有非封闭区域内的0元素，将其做上标记，在用for循环进行寻找，记录剩余每个区域内零的数量，通过标记的不同来区分是否属于同一个区域，用当前数量和最大值比较，若当前数量大，则记录该区域的颜色标记。

代码

include
#include
using namespace std;
int n;
int a[32][32];
int dir[4][2] = { {0,1},{1,0},{0,-1},{-1,0} }; //下右上左
int cnt = 0; //记录封闭区域的大小
int maxn = 0; //最大封闭区域的大小
int id = 2;
int max_id; //记录最大封闭区域的颜色标记
struct node
{
int x, y;
};
int bfs1(int x,int y) //广度优先查找
{
queue q;
node c;
c.x = x;
c.y = y;
cnt = 0;
q.push(c); //压入队列
int dx, dy;
while (!q.empty())
{
node m = q.front(); //队列最前面的位置
for (int i = 0; i < 4; i++) //按顺序查找
{
dx = m.x + dir[0][i];
dy = m.y + dir[1][i];
if (dx >= 0 && dx <= n + 1 && dy >= 0 && dy <= n + 1 && a[dx][dy] == 0) //满足条件的0
{
a[dx][dy] = id; //符合条件做标记
node m1;
cnt++; //计数
m1.x = dx;
m1.y = dy;
q.push(m1); //可以继续搜索的位置，压入队列
}
}
q.pop(); //弹出
}
return cnt; //返回数量
}
int main()
{
int m = 0;
cin >> n;
for (int i = 0; i <= n; i++) //初始化，并且多增加一层0
for (int j = 0; j <= n; j++)
a[i][j]=0;
for (int i = 1; i <= n; i++) //输入
for (int j = 1; j <= n; j++)
cin >> a[i][j];
m=bfs1(0, 0); //先找到非封闭区域的0，并做上标记
for (int i = 1; i <= n; i++) //再次寻找各个封闭区域内0的数量
for (int j = 1; j <= n; j++)
if (a[i][j] == 0)
{
id++;
m=bfs1(i, j);
if (m > maxn) //寻找最大封闭区域
{
maxn = m;
max_id = id; //记录最大封闭区域的颜色标记
}
}
for (int i = 1; i <= n; i++) //输出
{
for (int j = 1; j <= n; j++)
if (a[i][j] == 1)
cout << 1 << ‘ ‘;
else if(a[i][j]==max_id) //最大封闭区域
cout << 2 << ‘ ‘;
else //其他区域的0
cout << 0<< ‘ ‘;
cout << endl;
}
system(“pause”);
return 0;
}
多说几句：

上面的分析有点问题，样例输出一下应该是这样，先把最外面的0全置2，然后再循环原本的矩阵，广搜，遇到一个0就先让标签（颜色）加一，给这个0和它的同一个封闭区域的0置为这个标签，递归的时候会统计这一轮染色了几个0，如果比最大的个数多，就更新，并且还要记录此时的标签，输出时，除了这个标签，别的全输出为0（1的话正常输出就好了）。

例题2

题目同上，只是不再只是涂最大格子，而是涂所有封闭格子
思路同上，更加简单，先涂完外围一圈，再遍历矩阵，把0的全涂成2就行了，具体看代码

代码

include
using namespace std;
const int f[4][2]={{-1,0},{0,1},{1,0},{0,-1}};
int n,a[35][35],b[35][35];
bool check(int x,int y){
if(x<0||x>n+1||y<0||y>n+1) return 0;
return !a[x][y];
}
void DFS(int t,int x,int y){
a[x][y]=t;
for(int i=0;i<4;i++)
if(check(x+f[i][0],y+f[i][1])) DFS(t,x+f[i][0],y+f[i][1]);
}
int main(){
scanf(“%d”,&n);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++) scanf(“%d”,&a[i][j]),b[i][j]=a[i][j];
DFS(1,0,0);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(!a[i][j]) DFS(2,i,j);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)
if(a[i][j]==b[i][j]) printf(“1 “);else
if(a[i][j]==1) printf(“0 “);else printf(“2 “);
printf(“\n”);
}
return 0;
}

例题3

题目

有个电梯，每一层楼都可以停，只是算法混乱了，所以你得写个补丁；第i层楼(1<=i<=N)上有一个数字Ki(0<=Ki<=N)，表示上或下的层数（相对于当前层），每层楼都可以上或下。当然，如果不能满足要求（没有的层），相应的按钮就会失灵。例如：3 3 1 2 5代表了Ki（在第一层可以上或下3层；当然下是不可能的，第三层可以上或下1层），从一楼开始。在一楼，按“上”可以到4楼，按“下”是不起作用的，因为没有-2楼。那么，从A楼到B楼至少要按几次按钮？

输入要求

共二行。 第一行为3个用空格隔开的正整数，表示 N,A,B（共基层，开始层，结束层）；(1≤N≤200, 1≤A,B≤N)N,A,B(1≤N≤200,1≤A,B≤N)。 第二行为N个用空格隔开的非负整数，表示每层按钮的数值Ki。

输出要求

一行，即最少按键次数；若无法到达，则输出−1。

输入样例

5 1 5
3 3 1 2 5

输出样例

3

代码

include
using namespace std;
//bfs求最少次数
int vis[250];//vis表示该楼层是否到达过
int flor[250];

struct elevator{
int id;//代表楼层号
int step;//代表走的几步
}begin;

int main()
{
int N,A,B;
scanf(“%d %d %d”,&N,&A,&B);
for(int i=1;i<=N;i++)
{
scanf(“%d”,&flor[i]);
}
queue p;
begin.id=A;
begin.step=0;
p.push(begin);//初始入队
elevator e;
while(!p.empty())
{
e=p.front();
if(e.id==B) break;
p.pop();
if(e.id+flor[e.id]<=N&&!vis[e.id+flor[e.id]])//题目中说明可到达楼层在1~N之间，故可作为判定的条件
{
vis[e.id+flor[e.id]]=1;
p.push((elevator){e.id+flor[e.id],e.step+1}); //如果可行，就入队列
}
if(e.id-flor[e.id]>=1&&!vis[e.id-flor[e.id]])
{
vis[e.id-flor[e.id]]=1;
p.push((elevator){e.id-flor[e.id],e.step+1});
}
}
if(e.id==B) printf(“%d”,e.step);//判定是一位有解输出还是误无解循环终止导致输出
else printf(“-1”);
return 0;
}

思想（布线问题）

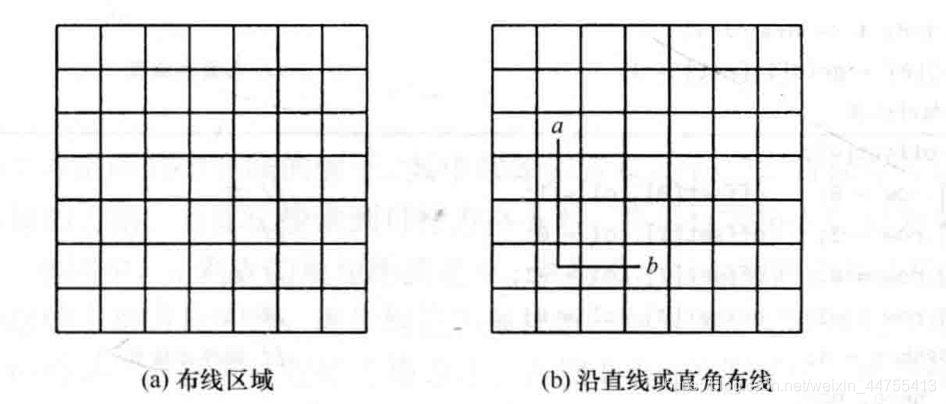
印刷电路板将布线区域划分成nxm个方格阵列，如图1所示。精确的电路布线问题要求确定连接方格a的中点到方格b的中点的最短布线方案。在布线时，电路只能沿直线或直角布线， 如图2所示。为了避免线路相交，已布了线的方格做了封锁标记，其他线路不允许穿过被封锁的方格。

题目分析

这个问题很类似迷宫问题，因此我们可以使用回溯法来解决，这里稍微提一下，如果使用回溯法，那么解空间将是一颗子集树。
但是这里我们还是决定使用分支限界法，因为回溯法是深度优先，它会一条路走到黑，然后计算出一条路径，然后回到起点，换一条路走到黑，再计算出一条路径，看是否更短…需要不停地走到进头再回溯，然后再次走到尽头。
但是分支限界法，是一种广度优先，它会每次寻找一层，不需要只选择一条路一直走。这样每一层的所有结点都会被加入队列。我们一层一层地寻找，先遇到目标点的就是最短路径，也不需要回溯了。因为大家从同一起点出发，哪一条先到了说明哪一条最短。这也确实是分支限界法的思想——使用队列或者优先队列。
剩下的就是这个题目的细节处理了。我们怎么表示某个格子已经有围墙了，哪个格子没有呢？又如何去标志目前的路径长度呢？
我们知道，分支限界法是广度优先搜索，所以每一层的路径长度都是相等的，区别在于某一条路径在同一层可能已经到了目标点。明确了这一点我们就知道了，处于遍历过程中同一层的所有格子都具有相同的路径长度，所以我们可以将其一起记录下来，直接填在我们的nm表格中即可.
于是我们声明一个nm的二维矩阵grid，用1表示这里有围墙，不能填入，用0表示可以填入。于是根据迷宫问题的思路，我们预处理的时候将表格的四条边全部填为1，因为四条边上的点是不会到达目标点的，而且它们都是尽头的点，不需要再去访问填充了。将起始点的邻居从2开始标记，下一层是3，再下一层是4…依次类推，最终到终点的填充数-2即可得到最短路径长度。

由于我们只能走直角或者直线，所以我们只看上下左右四个方向即可。所以只需要给出一个增量数组，表示这四个方向。
剩下的细节，比如创立一个结构体position来表示每个方格的位置，属性为row和col。初始时，判断start和finish是否相等，如果相等可以直接返回，表示我们已经找到了最终的位置。
等我们计算出了最终的最短路径，我们可以通过向前回溯的方法，找到最短路径的中间方格。将结束位置当作当前位置，用j表示当前路径长度,0<=j<=路径长度-1仍然用之前的增量数组寻找邻居格子nbr，如果发现邻居格子填充的值为j+2，则可以退出当前邻居的查找，将其记录进path数组，准备找寻第二个邻居…依次类推，直到j=0.我们就找到了最终的具体路径和最短路径长度。

代码部分

include
#include
using namespace std;
//定义一个表示电路板上方格位置的结构体
struct Position
{
int row;
int col;
};
//计算从起始位置start到目标位置finish的最短布线路径
//start为起始位置,finish为目标位置,PathLen为路径长度,path为一个数组,表示经过的路径
//n为行数,m为列数
bool FindPath(Position start,Position finish,int& PathLen,Position* &path,int m,int n)
{
int grid[n+1][m+1];
//如果初始位置和目标位置重合,就直接返回
if((start.row==finish.row) && (start.col==finish.col))
{
PathLen = 0;
return true;
}
//对四个边缘进行建立围墙,方格值为1表示不允许布线,标志为0可以布线
for(int i = 0;i <= m+1;i++)
grid[0][i] = grid[n+1][i] = 1;
for(int j = 0;j <= n+1;j++)
grid[j][0] = grid[j][m+1] = 1;
Position offset[4];//设置4个偏移量,我们要向4个方向查找遍历
//我们以右-下-左-上的方向遍历
offset[0].row = 0;offset[0].col = 1;
offset[1].row = 1;offset[1].col = 0;
offset[2].row = 0;offset[2].col = -1;
offset[3].row = -1;offset[3].col = 0;
int numofnbrs = 4;//邻居的数目
Position here,nbr;//表示此时所在的方格位置以及它的邻居
here.row = start.row;
here.col = start.col;
grid[start.row][start.col] = 2;//初始化位置定为2
queueQ;//建立方格队列,邻居存入
int flag = 0;//标志位
do
{
for(int i = 0;i < numofnbrs;i++)
{
nbr.row = here.row + offset[i].row;
nbr.col = here.col + offset[i].col;
if(grid[nbr.row][nbr.col]==0)
{
grid[nbr.row][nbr.col] = grid[here.row][here.col]+1;
if((nbr.row == finish.row) && (nbr.col==finish.col))
{
flag = 1;
break;//布线完成
}
Q.push(nbr);
}
}
if(flag)
break;//布线完成
//活结点队列是否非空
if(Q.empty())
return false;
Q.pop();//将上一扩展结点删除
here = Q.front();//取下一个扩展结点
} while (true);
//构造最短布线路径
PathLen = grid[finish.row][finish.col] - 2;
//定义路径
path = new Position[PathLen];
//回溯遍历找到路径
here = finish;
for(int j = PathLen - 1;j >= 0;j++)
{
path[j] = here;
for(int i = 0;i < numofnbrs;i++)
{
//找前驱位置
nbr.row = here.row + offset[i].row;
nbr.col = here.col + offset[i].col;
if(grid[nbr.row][nbr.col] == j + 2)
break;//找到了路径上的前一个点
}
here = nbr;
}
return true;
}