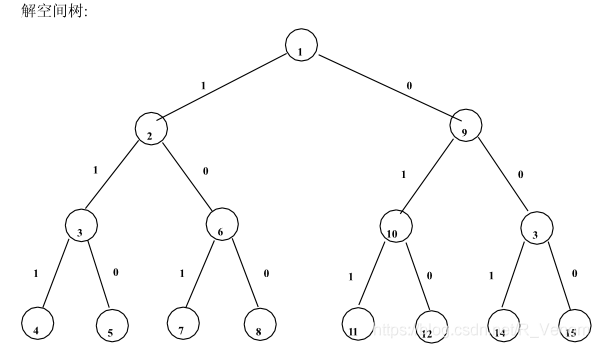
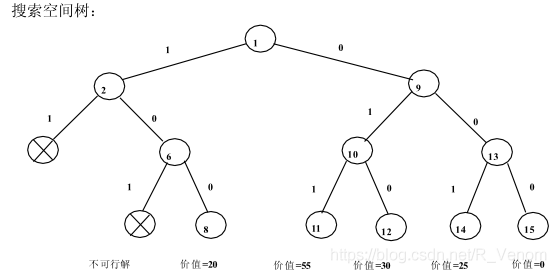
其实我是不想写这种很功利的东西的，但是要挂科啦！挂科!好了，下面直奔主题
算法的5个属性：
有穷性:一个算法必须总就是在执行有穷步之后结束,且每一步都在有穷时间内完成。
确定性:算法中每一条指令必须有确切得含义。不存在二义性。只有一个入口与一个出口
可行性:一个算法就是可行得，就是算法描述得操作就是可以通过已经实现得基本运算执行有限次来实现得。
输入:一个算法有零个或多个输入,这些输入取自于某个特定对象得集合。
输出:一个算法有一个或多个输出,这些输出同输入有着某些特定关系得量。
image.png
4．对解空间树进行深度优先搜索的是( A )。
A．回溯算法 B．分支限界算法 C．分治算法
D．动态规划算法
6．鬼牌除外的一副扑克牌，共有13种扑克牌，每种牌4张，不考虑花色，从中任取k张牌有多少种可能结果？该问题最适合的算法是（ C ）。
A．回溯算法
B．概率算法
C．动态规划算法
D．分治算法
7．如果一个问题采用贪心算法、动态规划算法、回溯算法、分支限界算法都可以得到最优解，对四种算法进行比较，你认为最有可能的是（ B ）。
A．动态规划算法效率最高
B．贪心算法效率最高
C．回溯算法效率最高
D．分支限界算法效率最高
8．下面关于回溯算法与分支限界算法的描述，正确的是（ A ）。
A．前者不创建解空间树，后者创建解空间树
B．后者不创建解空间树，前者创建解空间树
C．两者均创建解空间树
D．两者均不创建解空间树8．下面关于回溯算法与分支限界算法的描述，正确的是（ A ）。
10．关于P类和NP类问题，下列说法正确的是（ A ）。
A．P类是容易处理的
B．NP类问题是不能处理的
C．P类=NP类
D．P类≠NP类
image.png
简答题
1．如果系统rand( )函数产生的随机数范围在[0,32767]，请写出表达式产生[a，b]范围随机整数【其中a，b均为整数，且b-a<32767】，请写出表达式产生[0,1]范围且小数点后含有3位的随机小数。
rand()%(b-a+1)+a
Rand()1001/1000
image.png
2．假设打印时间分别为6,3,8,1,4分钟的5个人同时排队等待一台打印机服务，一个人的等待时间=排在他前面的人的打印时间之和+自己的打印时间，为了求出使得所有人的等待时间总和最小的打印顺序，请给出一种贪心策略，并计算出所有人的等待时间之和。
贪心策略是时间短的先打印，等待时间之和15+34+43+62+81=49、
概率算法是一种非确定性地选择下一计算步骤的方法，（拉斯维加斯算法）算法不一定能得到解，但得到的一定是正确解，（ 舍伍德算法）算法主要目的是消除算法所需计算时间对输入实例的依赖。
程序是算法的具体实现，程序可以不满足算法的（有限性 ）性质。操作系统是一个无限循环执行的程序
决定算法复杂性的因素主要有 （求解问题的规模 ）、（具体的输入数据 ）和 （算法本身的设计 ）。
快速排序和合并排序策略上是相同的，都是用的（分治 ） 算法。
求最小生成树的 Prim 算法和 Kruskal 算法本质上都是（贪心）算法。
8、 分支限界法与回溯法都是在问题的解空间树 T 上搜索问题的解，二者（B）。
A．求解目标不同，搜索方式相同
B．求解目标不同，搜索方式也不同
C．求解目标相同，搜索方式不同
D．求解目标相同，搜索方式也相同
算法的复杂性等于（算法所需的计算资源）。
动态规划算法的基本要素为（ C）
A. 最优子结构性质与贪心选择性质
B．重叠子问题性质与贪心选择性质
C．最优子结构性质与重叠子问题性质
D. 预排序与递归调用
从活结点表中选择下一个扩展结点的不同方式将导致不同的分支限界法，以下除（ C）之外都是最常见的方式。
A．队列式分支限界法
B．优先队列式分支限界法
C．栈式分支限界法
D．FIFO 分支限界法
何谓P、NP问题
P问题指可以在多项式时间内求解的问题
NP问题（(Non-deterministic Polynomial Problem，非确定性多项式问题），指问题只能通过验证给定的猜测是否正确来求解。所谓多项式指的是验证猜测可在多项式时间内完成，所谓非确定性指的是问题只能通过验证猜测来解，而不能直接求解
回溯法的搜索特点是什么，其显著特性是什么？
深搜。
以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索，回溯法的本质是穷举】
何谓最优子结构性质
最优子结构性质就是能让转移到n的状态是最优的，并且与后面的决策没有关系，即让后面的决策安心地使用前面的局部最优解的一种性质
简单描述分治法、动态规划法、贪心算法的基本思想
分治法：将问题分解成多个子问题，并允许不断分解，使规模越来越小，最终可用已知的方法求解足够小的问题。
贪心算法：总是选择当前最优解，并不考虑整体最优（拥有最优子结构特性）
动态规划：将较大问题分解为较小的同类子问题，这一点上它与分治法和贪心法类似。动态规划法解决子问题重叠现象，利用最优子结构，自底向上从子问题的最优解逐步构造出整个问题的最优解。（具有最优子结构和重叠子问题）

回溯法解0-1背包问题：

image.png
image.png
image.png