分治法在子问题和子子问题等上被重复计算了很多次，而动态规划则具有记忆性，通过填写表把所有已经解决的子问题答案纪录下来，在新问题里需要用到的子问题可以直接提取，避免了重复计算，从而节约了时间，所以在问题满足最优性原理之后，用动态规划解决问题的核心就在于填表，表填写完毕，最优解也就找到。

最长公共子序列

原理

我们用Ax表示序列A的连续前x项构成的子序列，即Ax= a1,a2,……ax, By= b1,b2,……by, 我们用LCS(x, y)表示它们的最长公共子序列长度，那原问题等价于求LCS(m,n)。为了方便我们用L(x, y)表示Ax和By的一个最长公共子序列。让我们来看看如何求LCS(x, y)。我们令x表示子序列考虑最后一项
（1） Ax ＝ By
那么它们L(Ax, By)的最后一项一定是这个元素！
为什么呢？为了方便，我们令t = Ax = By, 我们用反证法：假设L(x,y)最后一项不是t，则要么L(x,y)为空序列（别忘了这个），要么L(x,y)的最后一项是Aa＝Bb ≠ t, 且显然有a < x, b < y。无论是哪种情况我们都可以把t接到这个L(x,y)后面,从而得到一个更长的公共子序列。矛盾！
如果我们从序列Ax中删掉最后一项ax得到Ax-1,从序列By中也删掉最后一项by得到By-1，(多说一句角标为0时，认为子序列是空序列)，则我们从L(x,y)也删掉最后一项t得到的序列是L(x – 1, y - 1)。为什么呢？和上面的道理相同，如果得到的序列不是L(x - 1, y - 1)，则它一定比L(x - 1, y - 1)短（注意L（，）是个集合！），那么它后面接上元素t得到的子序列L(x,y)也比L(x - 1, y - 1)接上元素t得到的子序列短，这与L(x, y)是最长公共子序列矛盾。因此L(x, y) = L(x - 1, y - 1) 最后接上元素t，LCS(Ax, By) = LCS(x - 1, y - 1) + 1。
（2） Ax ≠ By
仍然设t = L(Ax, By), 或者L(Ax, By)是空序列（这时t是未定义值不等于任何值）。则t ≠ Ax和t ≠ By至少有一个成立，因为t不能同时等于两个不同的值嘛！
（2.1）如果t ≠ Ax，则有L(x, y)= L(x - 1, y)，因为根本没Ax的事嘛。
LCS(x,y) = LCS(x – 1, y)
（2.2）如果t ≠ By,l类似L(x, y)= L(x , y - 1)
LCS(x,y) = LCS(x, y – 1)
可是，我们事先并不知道t，由定义，我们取最大的一个，因此这种情况下,有LCS(x,y) = max(LCS(x – 1, y) , LCS(x, y – 1))。看看目前我们已经得到了什么结论：
LCS(x,y) =
(1) LCS(x - 1,y - 1) + 1 （Ax ＝ By）
(2) max(LCS(x – 1, y) , LCS(x, y – 1)) （Ax ≠ By）
这是一个显然的递推式，光有递推可不行，初值是什么呢？显然，一个空序列和任何序列的最长公共子序列都是空序列！所以我们有:
LCS(x,y) =
(1) LCS(x - 1,y - 1) + 1 如果Ax ＝ By
(2) max(LCS(x – 1, y) , LCS(x, y – 1)) 如果Ax ≠ By
(3) 0 如果x = 0或者y = 0
到此我们求出了计算最长公共子序列长度的递推公式。我们实际上计算了一个(n + 1)行(m + 1)列的表格（行是0..n，列是0..m)，也就这个二维度数组LCS(,)。
现在问题来了，我们如何得到一个最长公共子序列而仅仅不是简单的长度呢？其实我们离真正的答案只有一步之遥！
仍然考虑那个递推式，我们LCS(x,y)的值来源的三种情况：
（1） LCS(x – 1, y – 1) + 1如果Ax ＝ By
这对应L(x,y) = L(x,- 1 y- 1)末尾接上Ax
（2.1） LCS(x – 1, y) 如果Ax ≠ By且LCS(x – 1, y) ≥LCS(x, y – 1)
这对应L(x,y)= L(x – 1, y)
（2.2） LCS(x, y – 1) 如果Ax ≠ By且LCS(x – 1, y) 这对应L(x,y) = L(x, y – 1)
（3） 0 如果 x =0或者y = 0
这对应L(x,y)=空序列
注意(2.1)和(2.2) ，当LCS(x – 1, y) ＝ LCS(x, y – 1)时，其实走哪个分支都一样，虽然长度时一样的，但是可能对应不同的子序列，所以最长公共子序列并不唯一。

例题

Description
给出两个字符串A B，求A与B的最长公共子序列（子序列不要求是连续的）。
比如两个串为：abcicba 和 abdkscab，则 ab是两个串的子序列，abc也是，abca也是，其中abca是这两个字符串最长的子序列。
Input
第1行：字符串A
第2行：字符串B
(A,B的长度 <= 1000)
Output
输出最长的子序列，如果有多个，随意输出1个。
Sample Input
abcicba
abdkscab
Sample Output
abca
思路：
此题的切入点就是动态规划，通过动归来确定哪些字符是最长公共子序列中的字符，mat[i][j] 表示第一个序列的前i个字符和第二个序列的前j个字符的公共子序列，动态转移方程为：
dp[i][j] = max(dp[i-1][j], dp[i][j-1],dp[i-1][j-1] + (A[i]==B[j] ? 1 : 0))，表示在这三种状态中取到最大值，
（1）第一种状态表示不录入第一个序列的第i个字符时的最长公共子序列，
（2）第二种状态表示不录入第二个序列的第j个字符时的最长公共子序列，
（3）第三种状态表示第一个序列的前i-1个字符与第二个序列前j-1个字符的公共子序列加上最后一个字符的录入状态，如果最后的一个字符相等则录入状态为1，否则为0。
然后根据动归的状态，来判断我们要求得的序列中的字符有哪些。

代码

include
#include
#include
#include
#include
#include
#include
#define INF 0x3f3f3f3f

using namespace std;

char a[1001], b[1001];
int dp[1001][1001], len1, len2;

void lcs(int i, int j)
{
for(i=1; i<=len1; i++)
{
for(j=1; j<=len2; j++)
{
if(a[i-1] == b[j-1])
dp[i][j] = dp[i-1][j-1] + 1; //dp存的是长度
else if(dp[i-1][j] > dp[i][j-1])
dp[i][j] = dp[i-1][j];
else
dp[i][j] = dp[i][j-1];
}
}
}

void llcs()
{
int i, j, z = 0;
char c[1001];
memset(c, 0, sizeof(c));
i = len1, j = len2;
while(i!=0 && j!=0)
if(a[i-1] == b[j-1])
{
c[z++] = a[—i];
j—;
}
else if(dp[i-1][j] < dp[i][j-1])
j—; //选dp[i][j-1],即不选j(j-1了)
else if(dp[i][j-1] <= dp[i-1][j])
i—;
}
for(i=z-1; i>=0; i—)
printf(“%c”, c[i]);
printf(“\n”);

}

int main()
{
while(~scanf(“ %s”, a))
{
scanf(“ %s”, b);
memset(dp, 0, sizeof(dp));
len1 = strlen(a);
len2 = strlen(b);
lcs(len1, len2);
llcs();
}
return 0;
}

最大子段和

题目描述

给出一段序列，选出其中连续且非空的一段使得这段和最大。

输入格式：
第一行：是一个正整数N，表示了序列的长度。
第二行：包含N个整数num[i]，描述了这段序列。

输出格式：
一个整数，为最大的子段和是多少。
输入样例：
7
2 -4 3 -1 2 -4 3
1
2
输出样例：
4
1
最大子段和
对于最大子段和这个问题，其实我们发现如果说序列中所有的数都是正数，那么最大子段和一定是所有数的和，但为什么有时候不是呢？这就是负数捣的鬼。那么怎么解决负数呢？这就要用到动态规划了，提到DP，就一定就要去想：状态、转移方程、初值和答案了。

用数组dp，这里可以假设dp[i]是最大字段和的最后一个，那么他肯定是前面的dp[i-1]和此位置的a[i]结合，或者是a[i]。
例如(-2,11,-4,13,-5,2)，这里我是下标从1开始，dp[0]的初值为无穷小，所以dp[1]就可以和dp[0]+a[1]和a[1]进行比较。所以此时dp[1]=-2，然后dp[2]的值就是11，以此类推dp[3]的值是7，dp[4]的值是20，dp[5]的值是15，dp[6]的值是17，得出dp方程为dp[i]=max(dp[i],d[i-1]+a[i])。

代码

include
#include
#include
#include
#include
#include

01背包

问题描述

给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包 的容量为C。问应如何选择装入背包的物品，使得装入背包中 物品的总价值最大?

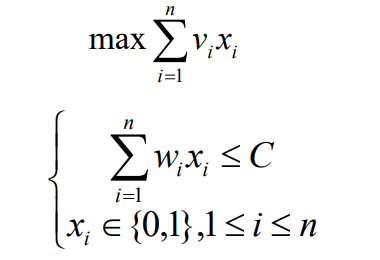
寻找递推关系式，面对当前商品有两种可能性：

• 包的容量比该商品体积小，装不下，此时的价值与前i-1个的价值是一样的，即V(i,j)=V(i-1,j)；
• 还有足够的容量可以装该商品，但装了也不一定达到当前最优价值，所以在装与不装之间选择最优的一个，即V(i,j)=max｛V(i-1,j)，V(i-1,j-w(i))+v(i)｝。

其中V(i-1,j)表示不装，V(i-1,j-w(i))+v(i) 表示装了第i个商品，背包容量减少w(i)，但价值增加了v(i)；
由此可以得出递推关系式：

• j<w(i) V(i,j)=V(i-1,j)
• j>=w(i) V(i,j)=max｛V(i-1,j)，V(i-1,j-w(i))+v(i)｝ | i（物品编号） | 1 | 2 | 3 | 4 | | —- | —- | —- | —- | —- | | w（体积） | 2 | 3 | 4 | 5 | | v（价值） | 3 | 4 | 5 | 6 |

填表，首先初始化边界条件，V(0,j)=V(i,0)=0；

然后一行一行的填表：

• 如，i=1，j=1，w(1)=2，v(1)=3，有j<w(1)，故V(1,1)=V(1-1,1)=0；
• 又如i=1，j=2，w(1)=2，v(1)=3，有j=w(1),故V(1,2)=max｛ V(1-1,2)，V(1-1,2-w(1))+v(1) ｝=max｛0，0+3｝=3；
• 如此下去，填到最后一个，i=4，j=8，w(4)=5，v(4)=6，有j>w(4)，故V(4,8)=max｛ V(4-1,8)，V(4-1,8-w(4))+v(4) ｝=max｛9，4+6｝=10……

所以填完表如下图：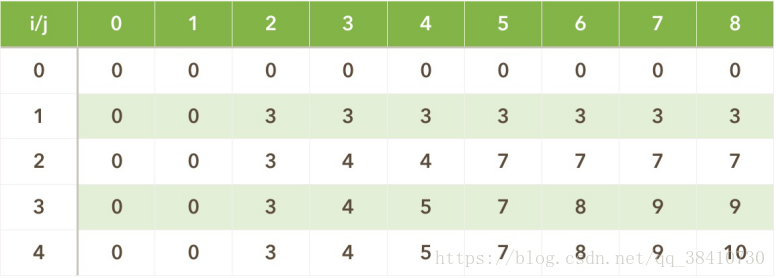


表格填完，最优解即是V(number,capacity)=V(4,8)=10。

代码实现

为了和之前的动态规划图可以进行对比，尽管只有4个商品，但是我们创建的数组元素由5个。
#include
using namespace std;
#include
int main()
{
int w[5] = { 0 , 2 , 3 , 4 , 5 }; //商品的体积2、3、4、5
int v[5] = { 0 , 3 , 4 , 5 , 6 }; //商品的价值3、4、5、6
int bagV = 8; //背包大小
int dp[5][9] = { { 0 } }; //动态规划表
for (int i = 1; i <= 4; i++) {
for (int j = 1; j <= bagV; j++) {
if (j < w[i])
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
}
}
//动态规划表的输出
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 9; j++) {
cout << dp[i][j] << ‘ ‘;
}
cout << endl;
}
return 0;
}

三角形

我自己做的时候求了最大的一条路径，无伤大雅，改个符号的事，思路如下：
从倒数第二行开始从左到右遍历每个数据，如果在它下面一行的左边的数比右边的大，那肯定选左边那个，然后把左边的值加到这个位置来，然后去操作同一行的下一个数一直到顶，其实数组下标从上到下是变小的，输出这条路劲的话又得从上到下，比较左右两个数谁大，就输出哪个，如果你取了右边那个，有一个标签（一开始置0）就得加一，你去下一行的时候数组下标就是这个标签，再比较左右大小。感觉动态规划很喜欢从后往前做，然后输出路径的时候又从前往后了。
#include “stdafx.h”
int main(int argc, char* argv[])
{
int i,j,n;
int a[100][100]; //用于存放三角形
int b[100][100]; //用于复制a数组
printf(“请输入数字三角形的行数：\n”);
scanf(“%d”,&n); //获取输入的行数
printf(“请输入数字三角形：\n”);
for(i=1;i<=n;i++){
for(j=1;j<=i;j++){
scanf(“%d”,&a[i-1][j-1]); //输入三角形
b[i-1][j-1]=a[i-1][j-1]; //复制
}
}
for(int row=n-2;row>=0;row—){ //从倒数第二行开始往上递推
for(int col=0;col<=row;col++){
if(a[row+1][col]>a[row+1][col+1]){ //将每个数下面的两个数进行比较
a[row][col]+=a[row+1][col]; //取较大的数加
}
else{
a[row][col]+=a[row+1][col+1];
}
}
}
printf(“路径总和最大为：\n”);
printf(“%d\n”,a[0][0]);
printf(“自顶向下的路径为:\n”);c
printf(“%d “,b[0][0]); //先输出第一行的数字
int l=0;//定义列
for(int m=1;m if(a[m][l]>a[m][l+1]){
printf(“%d “,b[m][l]); //根据数值较大的数的位置输出b数组中指定位置的值
}else{
printf(“%d “,b[m][l+1]);
l=l+1; //如果较大的数为右边的数则下次开比较的列加1
}
}
printf(“\n”);
return 0;
}