分类

数值随机化算法、蒙特卡罗算法、拉斯维加斯算法、舍伍德算法
数值随机化算法:近似解
蒙特卡罗算法:解未必正确
拉斯维加斯算法:正确解、会找不到解，改进有效性
舍伍德算法:正确解、总能找到，时间复杂性均衡，消除特例对算法效率的影响

随机数

随机数在概率算法设计中扮演着十分重要的角色。在现实计算机上无法产生真正的随机数，因此在概率算法中使用的随机数都是一定程度上随机的，即伪随机数。
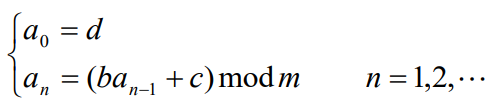
线性同余法是产生伪随机数的最常用的方法。由线性同余法产生的随机序列image.png满足
image.png
其中b>0，c>0,d<=m。d称为该随机序列的种子。如何选取该方法中的常数b、c和m直接关系到所产生的随机序列的随机性能。这是随机性理论研究的内容，已超出讨论的范围。从直观上看，m应取得充分大，因此可取m为机器大数，另外应取gcd(m,b)=1，因此可取b为一素数。

舍伍德算法:随机洗牌

image.png
我的理解是随机数（这个随机数的上限加上i还不能超过n，毕竟总共就n张牌）求出来之后加了i，所以得到的是i后面的某张牌的下标 。别的方法可以i从后往前开始，然后，j=n-rnd.Random(n-i),这样就是和前面的某一张牌互换了。
不过，在讲到洗牌这个算法的时候，我其实脑子里第一个想到的还是交叉洗牌的方式，将牌分为两堆，轮流将两边的牌压入新的数组，两堆牌都随机产生一个随机数，即每次那堆牌放多少张去新数组，再设置一个cnt，如果哪边已经连续三轮（这个轮数可以自己定，拍脑袋的数字嘛）没有放牌进数组了，因为可能随机数是0，也就是不放牌进去，就强制把这一堆牌的第一张牌放进数组，重置cnt（cnt从3变为0），接着洗。
老师还讲了一种抽牌的洗牌方式，没有仔细想过，我觉得就是产生一大一小两个随机数作为抽出来的那堆牌的起始和结束。再把这堆排放到最后面，多抽几次也能达到洗牌的目的。
求圆周率和定积分
double Darts(int n) {
//用随机投点法计算π值
static RandomNumber dart;
int k = 0;
for (int i = 1; i <= n; i++) {
double x = dart.fRandom();
double y = dart.fRandom();
if ((xx + yy) <= 1) k++;
}
return 4 * k / double(n);
}

double Darts(int n) {
//用随机投点法计算定积分
static RandomNumber dart;
int k = 0;
for (int i = 1; i <= n; i++) {
double x = dart.fRandom();
double y = dart.fRandom();
if (y <= f(x)) k++;
}
return k / double(n);
}