前情回顾

OK，第7篇运用了多边形三角剖分+向量叉积的方式计算多边形面积。初步见到了三角形剖分化繁为简的能力，这一篇算是此种算法思想的延伸——质心计算。
质心坐标怎么能和面积计算扯上关系呢？
下面来一一分解。

质心

什么是质心？就是通过该点，区域达到一种质量上的平衡状态。
质量中心简称质心(Centroid)，指物质系统上被认为质量集中于此的一个假想点。可能物理学上讲的比较多，简单点说就是规则几何物体的中心，不规则的可以通过挂绳子的方法来寻找。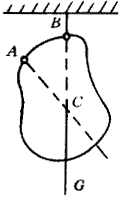
image.png
与重心不同的是，质心不一定要在有重力场的系统中。值得注意的是，除非重力场是均匀的，否则同一物质系统的质心与重心通常不在同一假想点上。
在我们的生活经验里，一个物体，如果想拿起它，我们更倾向于伸手去拿这个物体质量相对更集中的地方，因为这样会使物体保持平稳。往往物体的质心也就存在于此处。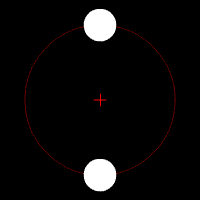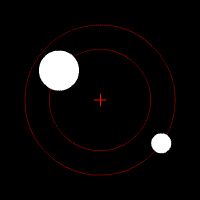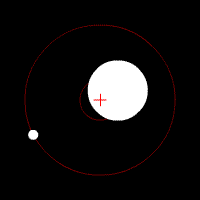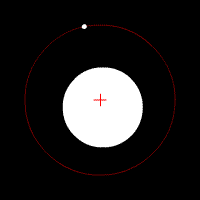
质心.gif
同样地，在一个多边形中，我们假设这个多边形的“材质”是均匀的，那么影响这个多边形质量分布情况的就只有面积。面积大的区域，质量更大，质心就越有可能向这个区域靠近。
那么基于我们对质心的感官理解，计算也自然有了方向。

质心的计算

在【上一篇】内容中我们已经实践过，将多边形分割为多个三角形，通过计算每个三角形的面积得出多边形的总面积。这个方法，同样适用于今天的质心计算。
这里先给出一个公式：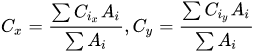
image.png
平面多边形X被剖分为i个简单图形X1,X2,▪▪▪,Xi，每个简单图形的重心点为Ci ，面积为Ai，那么这个平面多边形的重心点坐标为(Cx,Cy)。
这里多边形就可被分割为多个三角形。其中每个三角形的重心计算方式：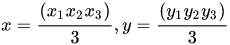
image.png
所以，以三角形剖分多边形的计算方式可以整理为：
计算每个三角形重心的横（纵）坐标，并与该三角形的面积作乘积，最终将每个乘积加和与总面积作除，即为质心的横（纵）坐标。

质心计算的实现

与上篇类似，将质心计算方法定义在了算法类Algorithm当中，定义了Centroid方法，并接受一个顺序给出的节点对象列表参数，用以计算质心坐标。

  1. public static Vertex Centroid(List<Vertex> vertexes)
  2.  {
  3.   //多边形总面积
  4.   double area = 0.0;
  6.   //质心
  7.   double Cx = 0.0;
  8.   double Cy = 0.0;
  10.   //取多边形第一个节点为剖分点
  11.   Vertex v0 = vertexes[0];
  13.   for (int i = 1; i < vertexes.Count - 1; i++)
  14.   {
  15.     //三角形两边向量
  16.     Vertex v1 = new Vertex(
  17.       vertexes[i].x - v0.x, vertexes[i].y - v0.y);
  19.     Vertex v2 = new Vertex(
  20.       vertexes[i + 1].x - v0.x, vertexes[i + 1].y - v0.y);
  22.     //面积
  23.     double A = (v1.x * v2.y - v2.x * v1.y) / 2;
  24.     area += A;
  26.     //三角形重心
  27.     double x = 0 + v1.x + v2.x; //x=(x1+x2+x3)/3
  28.     double y = 0 + v1.y + v2.y; //y=(xy+y2+y3)/3
  30.     //加权面积
  31.     Cx += A * x;
  32.     Cy += A * y;
  33.   }
  35.   Cx = Cx / area / 3 + v0.x;
  36.   Cy = Cy / area / 3 + v0.y;
  38.   return new Vertex(Cx, Cy);
  39.  }

这里，为了保证结果精度有两处处理：
1、不取原点为三角形剖分点，取顺序节点的第一点作为剖分点
2、计算三角形重心不在每次循环中除3，在循环结束后统一除以3
两处都是为了减少小数计算的舍入误差，与原算法上没有差别。

更完善的Polygon

现在的Polygon类，继实现面积计算之后，可以再加入质心计算了。下面是加入了质心属性的Polygon：

  1. public class Polygon : Geometry
  2.  {
  3.   private List<Vertex> vertexes =
  4.     new List<Vertex>();
  6.   public Polygon() { }
  8.   public Polygon(List<Vertex> vertexes)
  9.   {
  10.     this.vertexes = vertexes;
  11.     base.extent = new Extent(vertexes);
  12.     base.centroid = Algorithm.Centroid(vertexes);
  13.   }
  15.   public List<Vertex> Vertexes
  16.   {
  17.     get { return vertexes; }
  18.   }
  20.   public double Area
  21.   {
  22.     get
  23.     {
  24.       //返回面积的绝对值
  25.       return Math.Abs(
  26.         Algorithm.SignedArea(vertexes));
  27.     }
  28.   }
  30.   public override void Draw(Graphics graphics, Map map)
  31.   {
  32.     System.Drawing.Point[] points =
  33.       new System.Drawing.Point[vertexes.Count];
  35.     for (int i = 0; i < points.Length; i++)
  36.     {
  37.       points[i] = map.ToScreenPoint(vertexes[i]);
  38.     }
  39.     graphics.FillPolygon(
  40.       new SolidBrush(Color.LightSeaGreen), points);
  42.     //在界面绘制质心点
  43.     System.Drawing.Point cPoint = map.ToScreenPoint(centroid);
  44.     graphics.FillEllipse(new SolidBrush(Color.Red),
  45.       new Rectangle((int)cPoint.X, (int)cPoint.Y, 4, 4));
  47.     //在界面绘制质心坐标
  48.     graphics.DrawString(
  49.       String.Format("X:{0}\r\nY:{1}", centroid.x, centroid.y),
  50.     new Font("宋体", 17),
  51.     new SolidBrush(Color.Navy),
  52.     new PointF(cPoint.X, cPoint.Y));
  53.   }
  54. }

做个验证

绘制了两个shp多边形，一个质心在内，一个质心在外。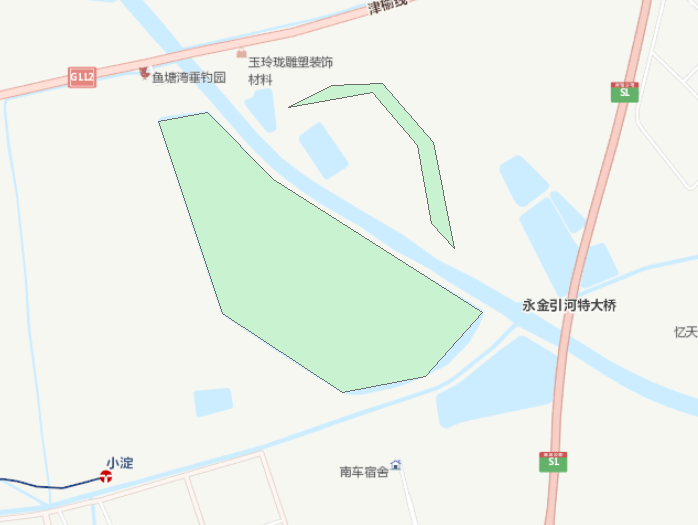
image.png
点击打开，读取shp进入地图程序，计算显示质心坐标：
image.png
可以看到两个质点的坐标值，对比一下ArcMap的质点坐标计算结果：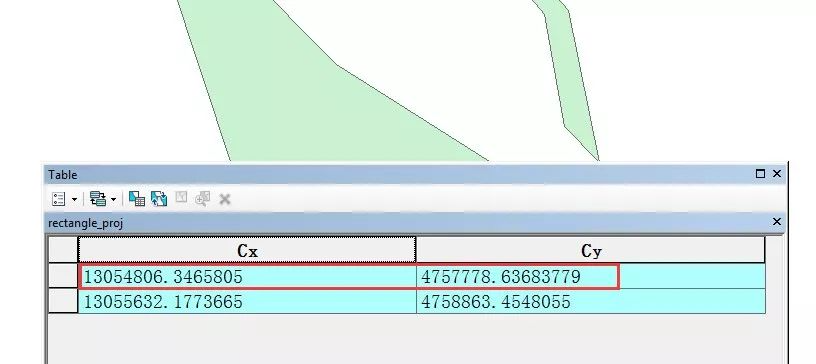
image.png
可以再次认为：我们的计算是准确的！
OK，多余的不再多说。基本属性的计算暂时告一段落，之后还会有更深入的算法实践。
在下一篇我会继续回到GIS组件的设计上来，逐步完善GIS组件的功能结构。

看好关注，下期见！

转载于公众号：GIS底层直通