支持向量机（Support Vector Machine，SVM）算法兼具形式优美和高效好用，难得地受到了跨学术界和工业界的好评。

一、SVM 算法介绍

在支持向量机中有三个重要概念，也是组成支持向量机的重要构件：

• 最大间隔
• 高维映射
• 核方法

这三个部件是彼此独立又互相关联的关系，他们在一起共同成就了SVM算法。

1.1. 距离是不同类别的天然间隔

数据点的“位置”实质是在不同维度有着不同现实含义的信息。

在分类时若想提高鲁棒性，就得多留点余地，也就是给正负类两边都多留点，使得分割线距离两边都达到最大间隔。

1.2. 何为支持向量

在任何分类任务中，只要找到两种不同类别之间的间隔，就能把两个类分开。

让间隔最大化，也就是让间隔变得“最胖”，就是支持向量机的目标。
间隔分为两种：

• 硬间隔：要求决不允许有例外
• 软间隔：允许有一些例外（比如两种颜色犬牙交错）

这些处于边缘的数据点就成为支持向量。支持向量是支持向量机的关注焦点。因为只要将它们正确分类，剩下的肯定也可以正确分类啦。

1.3. 从更高维度看线性不可分

在很多情况下，不同类别的数据分布并不想象棋那样泾渭分明，而是会混杂在一起，无法用线性加以区分，术语上很形象地称之为“线性不可分”。

支持向量机创造性地引入高维映射来巧妙地解决这个问题。

线性不可分只是在当前维度下不可分，但如果增加了维度，原本不可分的也就可分了。还是以刚才的围棋为例，顾名思义，围棋棋子都是黑白子互相包围在一起，属于线性不可分。但假设有一个武林高手暗运掌力，忽然快速往棋盘上一拍，让白子黑子都垂直往上飞起，同时让黑子飞高一点，白子则相对低一些，这样，平面无法线性区分的黑白子在进入立体空间，多了高度这个维度之后就体现出了区别。这时，只要往飞升的黑白子之间塞入一张薄纸，就把两种棋子分开了。二维称“线”,三维称“面”,超过三维的就不另外改名字了，统一称“超平面”。

知道当前分布是什么样子，也知道想要达到的分布是什么样子的，那么，就只要选择合适的映射函数了，也就解决了第二个问题。

二、支持向量机的算法原理

2.1. 算法基本思路

1. 最大间隔

支持向量机的原理说容易也真是容易，说不容易也真不容易。支持向量机说到底就是一种“线性分类器”,它以“间隔”作为损失的度量，标通过整多维的“直线”一超平面，使得间隔最大化。所谓“支持向量”,就是所有数据点中直接参与计算使得间隔最大化的几个数据点，这是支持向量机的得名由来，也是支持向量机的全部核心算法。

2. 高维映射

高维映射被许多教程说得神乎其神，但前面我们已经一再解释过它的原理。其核心就是通过映射，把线性不可分的数据变成线性可分，具体来说就是增加维度，如把原本成一条直线的正负样本点“掰弯”,或者给原本平铺在同一平面上互相包围的正负样本点添加一个“漏勺”,也就是加了一维高度值，使得非线性分布出现了线性可分的差异，从而最终达到分离正负类的目的，实现用线性分类器对非线性可分样本点进行分类的。

3. 核函数

说到支持向量机，除非是选择只介绍间隔最大化，否则总是免不了提到核函数(Kernel Function)这个术语。“核函数”听起来很吓人，我第一次看到时还下意识地往原子能方面靠。其实，核函数并没有那么深奥，它与前面接触的 Logistics函数一样，功能就是映射，说穿了就是给线性“披”一层马甲，变成曲线或者曲面， Logistics函数就通过映射把直线变成了S型曲线。

核函数也一样。核函数不是一种函数，而是一类功能性函数，能够在支持向量机中完成高维映射这种功能的函数都称为核函数，也就是说，只要数学函数满足要求，就都可以被用作核函数。不过，无论哪种核函数，其最根本的目的就是完成高维映射，具体完成两项工作，一是增加空间的维度，二是完成对现有数据从原空间到高维空间的映射。也就是说，核函数和高维映射虽然在讲解时拆分成两个概念，其实都是一个过程，二者可以看作因和果的关系。我们必须首先选定一款核函数，才能通过核函数将数据集进行映射，从而得到高维映射的结果。

最后需要说明的是，核函数虽然是一类函数，具体有很多款式， Scikit-Learn-包中也提供了多种核函数的选择，但是在一次支持向量机的学习过程中，需要首先设置好选择哪种数学函数作为核函数，且在整个运行过程中都将使用这个函数进行高维映射，而不会随着学习的进程调整和改变具体的核函数。

4. 支持向量机的运行机制

高维映射用于解决线性不可分问题，可以理解为对数据的“预处理”。对于那些你中有我、间不容发的非线性分布数据，首先通过核函数映射至高维，映射后的数据集呈线性分布，为使用线性方法分类创造了条件。

最后归纳一下，使用支持向量机进行分类经过三个步骤：

1. 选取一个合适的数学函数作为核函数。
2. 使用核函数进行高维映射，数据点在映射后由原本的线性不可分变为线性可分。
3. 间隔最大化，用间隔作为度量分类效果的损失函数，最终找到能够让间隔最大的超平面，分类也就最终完成了。

5. 核技巧

当你看到这一段时，心里应该清楚两点，一是支持向量机就是一台线性分类器，二是这台线性分类器可以通过高维映射来解决非线性分布问题。解决了旧问题，新的问题也随之而来：能不能把高维映射独立出来，作为一种通用化的组件，将所有非线性分布的数据集转化成线性分布，然后随便再选择一种线性分类器完成分类呢?这个问题也就是支持向量机是否能拆分的问题。

这个想法是非常好的，很多新算法就是靠这种灵光闪现才得以最终出现。不过，支持向量机并不可以拆分，原因可以用软件工程来解释支持向量机为了兼顾理论的优雅和运行的高效，在设计上选择了紧耦合，使得两项看似可以独立完成的工作变得密不可分。
问题从何而来呢？完整的支持向量机包括了间隔最大化和高维映射，就像是一部悬疑大片的两条主线，单独拎出来看好像都没有问题，但合在一起问题就来了。又要间隔最大化又要高维映射，听起来鼓舞人心，可是细细一算就不难发现：维度越高意味着间 隔最大化的计算量越大，实际运行起来效率可能非常低下，可是如果要照顾效果而削减维度，可能无法完成非线性分布数据映射成线性分布这项重要任务。两条主线互相“打架”,若一条想要完美收场，另一条就只能草草收场，总是不尽如人意。

眼看大片就要“烂尾”,这时化腐朽为神奇的核函数再次出来救场。在支持向量机中，涉及“核”的术语实际上有三个，分别是核函数、核方法( Kernel Method)和核技巧(Kernel Trick),三个术语说复杂也复杂，不过说简单也简单，核方法和核技巧就是提出需求，核函数则是给出解答。换而言之，核函数是一石二鸟，实际上是完成了两项独立的任务。

• 任务一是完成核方法提出的要求，就是如何将低维非线性数据映射成高维数据，从而变成线性可分。前面我们反反复复介绍的其实就是核方法的内容，但这并不是核函数的全部内容。
• 任务二是完成核技巧提出的要求，之所以称为“技巧”,是因为核技巧主要是提高核方法的计算效率。前面我们将高维映射和间隔最大化认为是支持向量机的两大部分，按 照这种理解，数据应该首先完成高维映射，然后计算间隔，最后再进行间隔最大化，也因此产生了双主线“打架”的问题。

核技巧就是要解决这个问题。计算间隔涉及向量点积运算，如果先进行高维映射再 进行向量点积运算，这会导致运算量激增，尤其是高维向量运算，由于参加运算的维度增加了，运算量也会显著增加。

核技巧简化了这个过程：只需要输入原始向量就能通过核技巧计算直接得到正确的点积结果，而不用把两个向量分别完成高维映射，再进行点积运算，即将两项工作用数学技巧一次就完成。由于无论是目标函数还是决策函数都只涉及输入样本与样本之间的内积，这一运算特点使得我们在实际使用支持向量机算法进行学习时，不需要显式地完成高维映射操作，只需要事先定义核函数即可得到等价的结果，还避免了高维向量的运算，明显提高了运算效果。能够同时满足核方法和核技巧两项要求，才是核函数完整的工作内容。

2.2 SVM 的数学解析

1. 点到超平面的距离

支持向量机对间隔的定义很简单，就是作为支持向量的点到超平面的距离的和。

对于点到N维超平面的距离，可以用以下公式计算：

%7D%20%3D%20%5Cfrac%20%7B%5Comega%5ET%20x%5E%7B(i)%7D%20%2B%20b%7D%7B%7C%7C%5Comega%7C%7C%7D%0A#card=math&code=%5Cgamma%5E%7B%28i%29%7D%20%3D%20%5Cfrac%20%7B%5Comega%5ET%20x%5E%7B%28i%29%7D%20%2B%20b%7D%7B%7C%7C%5Comega%7C%7C%7D%0A)

2. 间隔最大化

这里省略推导过程，具体可参考其他教程，包含大量复杂的数学概念和运算。

这里只需要注意两点：

1. 支持向量机使用拉格朗日乘子法搭配SMO算法求得间隔最大
2. 转化式的末尾为计算 ,也就是两个向量的内积。正因为间隔最大化可以转化为向量内积的运算，才使得高维映射可以通过核技巧进行优化。

3. 核函数

高维映射实际上也是一种函数映射，在支持向量机中，通常采用符号来表示这个将数据映射到高维空间的函数，向量x经过高维映射后就变成了#card=math&code=%5CPhi%28x_i%29),这时超平面的表达式也就相应变成了%20%2B%20b#card=math&code=%5Comega%5ET%20%5CPhi%28x_i%29%20%2B%20b)。

不过，我们也已经观察到，在间隔最大化的运算中只使用了高维向量内积运算的结果，而没有单独使用高维向量，也就是说，如果能较为简单地求出高维向量的内积，同样可以满足求解间隔最大化的条件。我们可以假设存在函数K,能够满足以下条件：

%20%3D%20%3C%5CPhi(x_i)%20%5Ccdot%20%5CPhi(x_j)%3E%20%3D%20%5CPhi(x_i)%5ET%20%5CPhi(x_j)%0A#card=math&code=K%28x_i%2C%20x_j%29%20%3D%20%3C%5CPhi%28x_i%29%20%5Ccdot%20%5CPhi%28x_j%29%3E%20%3D%20%5CPhi%28x_i%29%5ET%20%5CPhi%28x_j%29%0A)

这里的函数K就是我们前面一再介绍的核函数。有了核函数，所有涉及%5ET%20%5CPhi(x_j)#card=math&code=%5CPhi%28x_i%29%5ET%20%5CPhi%28x_j%29)的内积运算都可以通过#card=math&code=K%28x_i%2C%20x_j%29)简单求出，这也就是为什么核函数需要一边完成核方法的高维映射，一边又要完成核技巧的求内积结果。对于已知的映射函数中，核函数是很容易计算的，但在大多数情况下，使用支持向量机时并不知道映射函数中的具体形式， 好在数学家已经证明，在这种情况下数学函数只需要满足几个条件，就同样可以作为核函数，也就确保了核函数的存在性。

2.2 SVM 算法的具体步骤

使用支持向量机算法，具体需要三步：

1. 选择核函数工风中
2. 核函数完成高维映射并完成计算间隔所需的内积运算，求得间隔。
3. 使用SMO等算法使得间隔最大。

三、SVM 算法的 Python 实现

在 Scikit-Learn-库中，支持向量机算法族都在 sklearn.svm包中，当前版本一共有8个类。看起来也与其他机器学习算法族一样似乎有不少变种，其实并不太一样，支持向量机算法总的来说就一种，只是在核函数上有不同的选择，以及用于解决不同的问题，包括分类问题、回归问题和无监督学习问题中的异常点检测，具体为：

• LinearSVC类：基于线性核函数的支持向量机分类算法。
• LinearSVR类：基于线性核函数的支持向量机回归算法。
• SVC类：可选择多种核函数的支持向量机分类算法，通过“kernel”参数可以传入“linear”””选择线性函数、传入“polynomial”选择多项式函数、传入“rbf”选择径向基函数、传人“sigmoid”选择Logistics函数作为核函数，以及设置“precomputed”使用预设核值矩阵。默认以径向基函数作为核函数。
• SVR类：可选择多种核函数的支持向量机回归算法。
• NuSVC类：与SVC类非常相似，但可通过参数“nu”设置支持向量的数量。
• NuSVR类：与SVR类非常相似，但可通过参数“nu”设置支持向量的数量。
• OneClassSVM类：用支持向量机算法解决无监督学习的异常点检测问题。

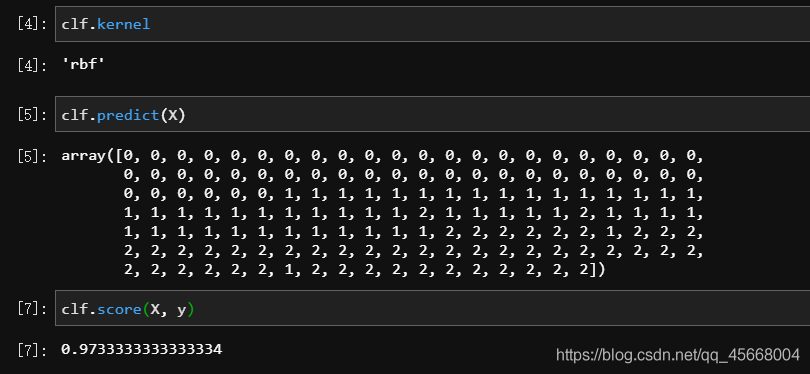
使用 SVC 类调用：

from sklearn.datasets import load_iris
from sklearn.svm import SVC
X, y = load_iris(return_X_y=True)
clf = SVC().fit(X, y)
clf.kernel  # 默认为径向量 rbf
clf.predict(X)
clf.score(X, y)

四、SVM 算法的优缺点

支持向量机算法最大的优点就在于可以用于解决非线性问题，同时，由于分类采用“支持向量”,训练不需要使用全部数据，它在小样本分类问题上有较好的表现。

核函数是支持向量机的一大核心装备，也是体现数学技巧的地方，但可谓“成也萧何败也萧何”,支持向量机目前仍然缺乏对非线性问题的通解，对于具体问题仍需要个案处理，在部分情况下要找到合适的核函数并不容易，这一限制使得支持向量机不那么易用。另外，原始的支持向量机使用间隔进行分类，因此只适合于二分类问题。