Scikit-Learn 中的 linear_model 是线性模型算法族库，本文将使用该库来实现基本的线性回归算法。

Scikit-Learn 对各类机器学习算法都进行了良好的封装，以线性回归算法为例，只需要以下简单三步便可以进行预测：

# 导入所需库
from sklearn import linear_model
# 训练线性回归模型
model = linear_model.LinearRegression()
model.fit(x, y)

在导入线性模型算法后，只需要利用 fit 方法为模型传入训练数据，完成模型的训练工作，就可以直接使用模型的predict方法，通过传入待预测的数据进行结果预测。

实现线性回归算法

1. 动手生成一个简单的数据集

%matplotlib inline
# 导入所需库
import matplotlib.pyplot as plt
import numpy as np
# 生成数据集
x = np.linspace(-3, 3, 30)  # 生成[-3, 3]区间内的30个点
y = 2 * x + 1
# 数据集绘图
plt.scatter(x, y)
plt.show()

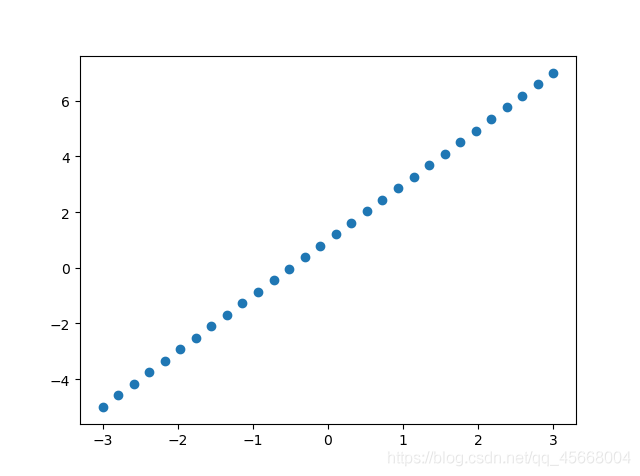
2. 数据整理

sklearn 中线性回归算法的fit方法需要传入的x和y是两组矩阵，每一行为同一个样本的信息，具体格式为：

x: [ [sample 1], [sample 2], [sample 3], ..., [sample n] ]

因此，我们需要对x和y做以下格式转变：

x = x.reshape((-1, 1))
y = y.reshape((-1, 1))

3. 开始训练

from sklearn import linear_model
# 训练线性回归模型
model = linear_model.LinearRegression()
model.fit(x, y)

4. 结果测试

x_ = np.array([[1], [2]])
model.predict(x_)

可以预测结果为 array([[3.], [5.]])，得到了正确结果。
我们还可以通过 model.coef_ 和 model.intercept_ 来查看这时的法向量 和截距 b。

当数据集中的数据存在随机扰动时：

现实中的数据并不能像上例数据中的那么理想，总会存在这样或那样的随机扰动，我们稍加改动以模拟这个过程：

x = x + np.random.rand(30)

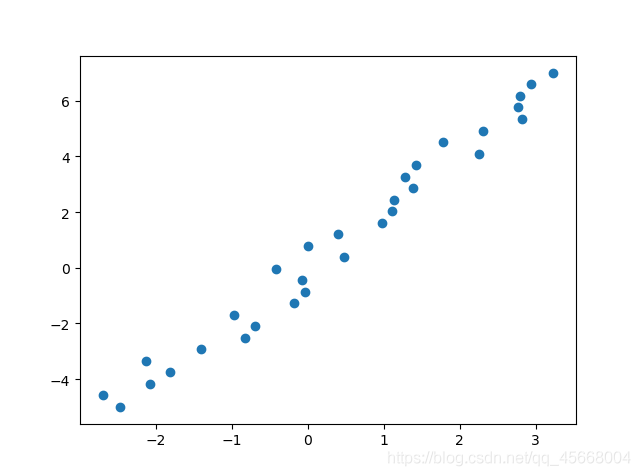
运行结果为：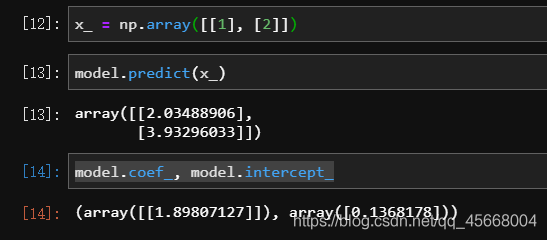

可以看出，加入随机扰动之后，线性回归模型对法向量 的学习还是比较准确的，但对于截距项就出现了较大的影响。