- 开始详细内容:
- 信息量:
- 熵:
- 相对熵(KL 散度):
- 交叉熵:
- JS 散度:
- KL 散度、JS 散度、Wasserstein 距离):">Wasserstein 距离(该部分摘自KL 散度、JS 散度、Wasserstein 距离):
- 郑华滨:令人拍案叫绝的 Wasserstein GAN)">WGAN 中对 KL 散度和 JS 散度的描述(摘自:郑华滨:令人拍案叫绝的 Wasserstein GAN)
目录:
- 信息量
- 熵
- 相对熵(KL 散度)
- 交叉熵
- JS 散度
- 推土机理论
- Wasserstein 距离
- WGAN 中对 JS 散度,KL 散度和推土机距离的描述
写在前面的总结:
1、目前分类损失函数为何多用交叉熵,而不是 KL 散度。
首先损失函数的功能是通过样本来计算模型分布与目标分布间的差异,在分布差异计算中,KL 散度是最合适的。但在实际中,某一事件的标签是已知不变的(例如我们设置猫的 label 为 1,那么所有关于猫的样本都要标记为 1),即目标分布的熵为常数。而根据下面 KL 公式可以看到,KL 散度 - 目标分布熵 = 交叉熵(这里的 “-” 表示裁剪)。所以我们不用计算 KL 散度,只需要计算交叉熵就可以得到模型分布与目标分布的损失值。
从上面介绍,知道了模型分布与目标分布差异可用交叉熵代替 KL 散度的条件是目标分布为常数。如果目标分布是有变化的(如同为猫的样本,不同的样本,其值也会有差异),那么就不能使用交叉熵,例如蒸馏模型的损失函数就是 KL 散度,因为蒸馏模型的目标分布也是一个模型,该模型针对同类别的不同样本,会给出不同的预测值(如两张猫的图片 a 和 b,目标模型对 a 预测为猫的值是 0.6,对 b 预测为猫的值是 0.8)。
注:交叉熵和 KL 散度应用方式不同的另一种解释(我更倾向于上面我自己的解释,更具公式解释性):
交叉熵:其用来衡量在给定的真实分布下,使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。这也是为什么在机器学习中的分类算法中,我们总是最小化交叉熵,因为交叉熵越低,就证明由算法所产生的策略最接近最优策略,也间接证明我们算法所算出的非真实分布越接近真实分布。
KL 散度(相对熵):衡量不同策略之间的差异呢,所以我们使用 KL 散度来做模型分布的拟合损失。
开始详细内容:
信息量:
任何事件都会承载着一定的信息量,包括已经发生的事件和未发生的事件,只是它们承载的信息量会有所不同。如昨天下雨这个已知事件,因为已经发生,既定事实,那么它的信息量就为 0。如明天会下雨这个事件,因为未有发生,那么这个事件的信息量就大。
从上面例子可以看出信息量是一个与事件发生概率相关的概念,而且可以得出,事件发生的概率越小,其信息量越大。这也很好理解,狗咬人不算信息,人咬狗才叫信息嘛。
我们已知某个事件的信息量是与它发生的概率有关,那我们可以通过如下公式计算信息量:
假设
是一个离散型随机变量,其取值集合为
, 概率分布函数
, 则定义事件
的信息量为:
熵:
我们知道:当一个事件发生的概率为
,那么它的信息量是
。
那么如果我们把这个事件的所有可能性罗列出来,就可以求得该事件信息量的期望,
信息量的期望就是熵,所以熵的公式为:
假设 事件
共有 n 种可能,发生
的概率为
,那么该事件的熵
为:
然而有一类比较特殊的问题,比如投掷硬币只有两种可能,字朝上或花朝上。买彩票只有两种可能,中奖或不中奖。我们称之为 0-1 分布问题(二项分布的特例),对于这类问题,熵的计算方法可以简化为如下算式:
相对熵(KL 散度):
相对熵又称 KL 散度, 如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x),我们可以使用 KL 散度(Kullback-Leibler (KL) divergence)来衡量这两个分布的差异。
在机器学习中,P 往往用来表示样本的真实分布,Q 用来表示模型所预测的分布,那么 KL 散度就可以计算两个分布的差异,也就是 Loss 损失值。
从 KL 散度公式中可以看到 Q 的分布越接近 P(Q 分布越拟合 P),那么散度值越小,即损失值越小。
因为对数函数是凸函数,所以 KL 散度的值为非负数。
有时会将 KL 散度称为 KL 距离,但它并不满足距离的性质:
- KL 散度不是对称的;
- KL 散度不满足三角不等式。
交叉熵:
我们将 KL 散度公式进行变形:
等式的前一部分恰巧就是 p 的熵,等式的后一部分,就是交叉熵:
在机器学习中,我们需要评估 label 和 predicts 之间的差距,使用 KL 散度刚刚好,即
,由于 KL 散度中的前一部分−H(y) 不变,故在优化过程中,只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做 loss,评估模型。
JS 散度:
JS 散度度量了两个概率分布的相似度,基于 KL 散度的变体,解决了 KL 散度非对称的问题。一般地,JS 散度是对称的,其取值是 0 到 1 之间。定义如下:
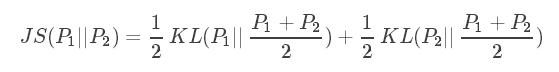
Wasserstein 距离(该部分摘自KL 散度、JS 散度、Wasserstein 距离):
KL 散度和 JS 散度度量的问题:
如果两个分配 P,Q 离得很远,完全没有重叠的时候,那么 KL 散度值是没有意义的,而 JS 散度值是一个常数。这在学习算法中是比较致命的,这就意味这这一点的梯度为 0。梯度消失了。
Wasserstein 距离度量两个概率分布之间的距离,定义如下
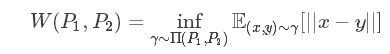
Π(P1,P2) 是 P1 和 P2 分布组合起来的所有可能的联合分布的集合。对于每一个可能的联合分布γ,可以从中采样 (x,y)∼γ得到一个样本 x 和 y,并计算出这对样本的距离 ||x−y||,所以可以计算该联合分布γ下,样本对距离的期望值 E(x,y)∼γ[||x−y||]。在所有可能的联合分布中能够对这个期望值取到的下界 infγ∼Π(P1,P2)E(x,y)∼γ[||x−y||]就是 Wasserstein 距离。
直观上可以把 E(x,y)∼γ[||x−y||]理解为在γ这个路径规划下把土堆 P1 挪到土堆 P2 所需要的消耗。而 Wasserstein 距离就是在最优路径规划下的最小消耗。所以 Wesserstein 距离又叫 Earth-Mover 距离。
Wasserstein 距离相比 KL 散度、JS 散度的优越性在于,即便两个分布没有重叠,Wasserstein 距离仍然能够反映它们的远近;而 JS 散度在此情况下是常量,KL 散度可能无意义。WGAN 本作通过简单的例子展示了这一点。考虑如下二维空间中的两个分布
和
,
在线段 AB 上均匀分布,
在线段 CD 上均匀分布,通过控制参数
可以控制着两个分布的距离远近。
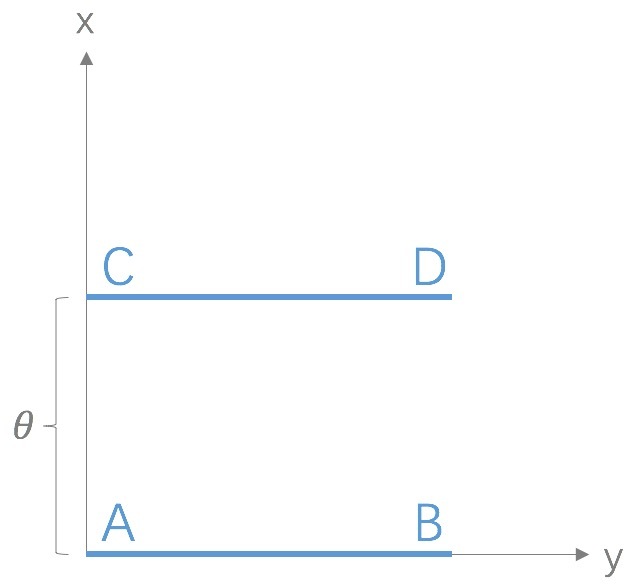
此时容易得到(读者可自行验证)
(突变)
(突变)
(平滑)
KL 散度和 JS 散度是突变的,要么最大要么最小,Wasserstein 距离却是平滑的,如果我们要用梯度下降法优化
这个参数,前两者根本提供不了梯度,Wasserstein 距离却可以。类似地,在高维空间中如果两个分布不重叠或者重叠部分可忽略,则 KL 和 JS 既反映不了远近,也提供不了梯度,但是 Wasserstein 却可以提供有意义的梯度。
WGAN 中对 KL 散度和 JS 散度的描述(摘自:郑华滨:令人拍案叫绝的 Wasserstein GAN)
假设
表示真实样本分布,
是由生成器产生的样本分布。原始 GAN 中:
判别器损失函数:
(公式 1)
生成器损失函数:
(公式 2)
(公式 3)
最优判别器:
首先根据公式 1,当生成器固定时,确定最优的判别器。对判别器进行求导,并令导数为 0,则:
化简得:
(公式 4)
从公式 4 也可以很容易看出最优判别器的特征:当
且
,最优判别器可以给出概率值 0,相反,最优判别器可以给出概率值 1。
生成器损失:
普通的 GAN 在训练时会有一个明显问题,即如果判别器训练的太好,生成器就会完全学不动;那么当判别器为最优时,我们可以通过公式推导生成器的损失函数是怎样。
生成器损失函数(1)
(公式 2)
首先给公式 2 添加一个不依赖生成器的项(真实分布损失:
):
添加该项后,上式变成了公式 1 的反,即最小化生成器损失变为了最大化判别器损失。代入最优判别器即公式 4,再进行简单的变换可以得到:
(公式 5)
根据 JS 散度的公式:
(公式 6)
于是公式 5 就可以继续写成:
(公式 7)
公式 7 即为生产器损失函数 1 在判别器最优条件下的值。
根据原始 GAN 定义的判别器 loss,我们可以得到最优判别器的形式;而在最优判别器的下,我们可以把原始 GAN 定义的生成器 loss 等价变换为最小化真实分布
与生成分布
之间的 JS 散度。我们越训练判别器,它就越接近最优,最小化生成器的 loss 也就会越近似于最小化
和
之间的 JS 散度。
问题就出在这个 JS 散度上。我们会希望如果两个分布之间越接近它们的 JS 散度越小,我们通过优化 JS 散度就能将
“拉向”
,最终以假乱真。这个希望在两个分布有所重叠的时候是成立的,但是如果两个分布完全没有重叠的部分,或者它们重叠的部分可忽略,那它们的 JS 散度就变成了
。
换句话说,无论
跟
是远在天边,还是近在眼前,只要它们俩没有一点重叠或者重叠部分可忽略,JS 散度就固定是常数
,而这对于梯度下降方法意味着——梯度为 0!此时对于最优判别器来说,生成器肯定是得不到一丁点梯度信息的;即使对于接近最优的判别器来说,生成器也有很大机会面临梯度消失的问题。
生成器损失函数(2)
(公式 3)
上文推导已经得到在最优判别器
下
(公式 9)
我们可以把 KL 散度(注意下面是先 g 后 r)变换成含
的形式:
(公式 10)
由公式 3,9,10 可得最小化目标的等价变形
注意上式最后两项不依赖于生成器 G,最终得到最小化公式 3 等价于最小化
(公式 11)
这个等价最小化目标存在两个严重的问题。第一是它同时要最小化生成分布与真实分布的 KL 散度,却又要最大化两者的 JS 散度,一个要拉近,一个却要推远!这在直观上非常荒谬,在数值上则会导致梯度不稳定,这是后面那个 JS 散度项的毛病。
(未完待续……)
参考:
https://blog.csdn.net/tsyccnh/article/details/79163834
https://blog.csdn.net/weixin_33869377/article/details/86808243
https://blog.csdn.net/zhangping1987/article/details/25368183

