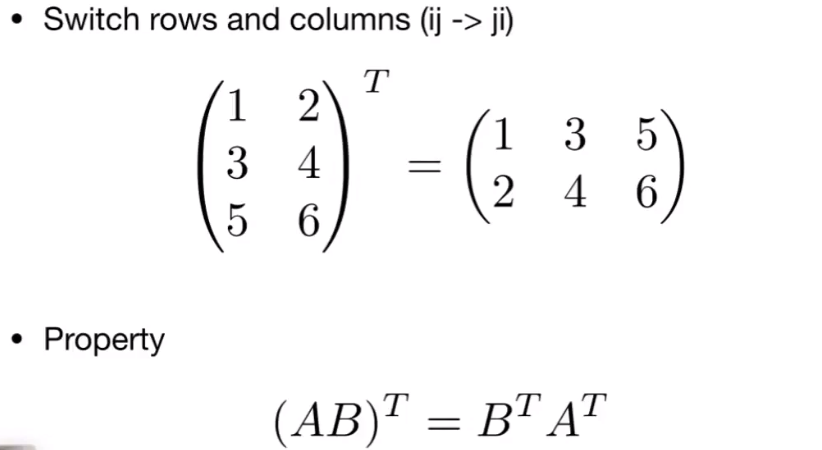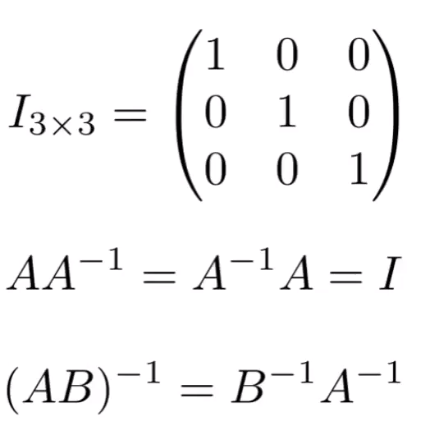Vector Multiplication
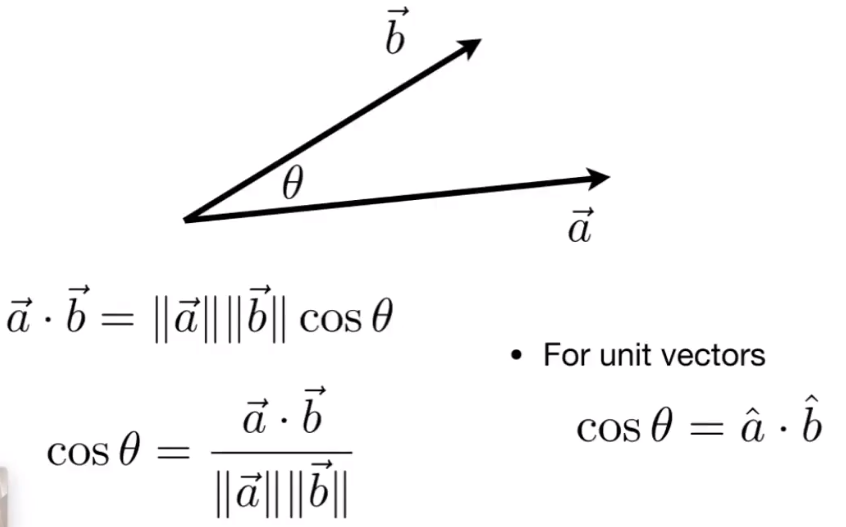
Dot Product 向量点乘
计算
矩阵形式
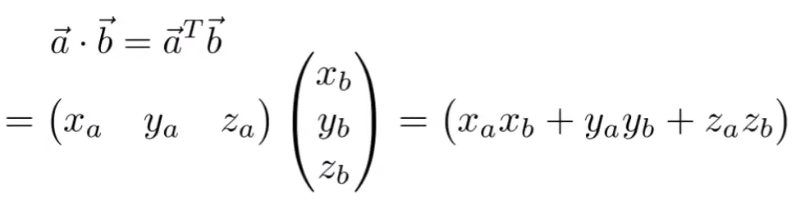
作用
- 找两个向量的夹角
- 找一个向量在另一个向量上的投影
- 分解向量
- 确定向量前后 可以知道向量在方向上有多接近
Cross Product 向量叉乘
定义
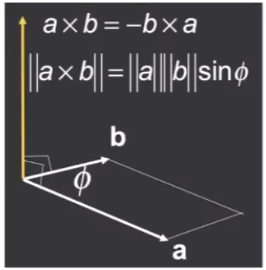
方向由右手螺旋定则确定，大小为形成的平行四边形面积。
性质
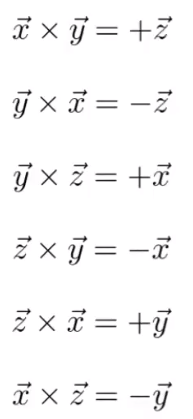
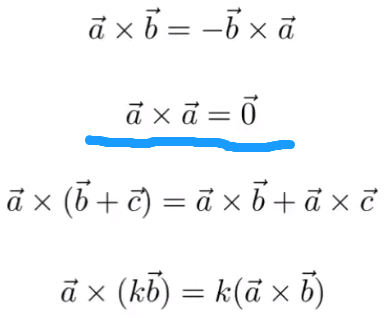
这门课里都是右手坐标系。
坐标表示
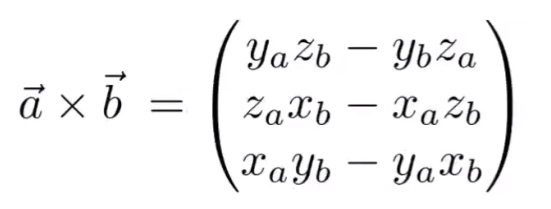
矩阵形式
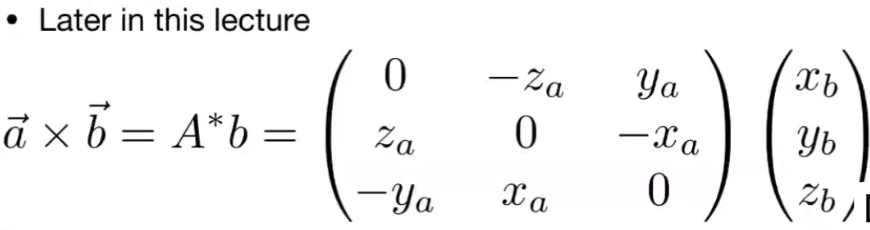
作用
- 判断左右 / 内外
左：如果 ab 叉积为正，则原点重合后向量 a 在向量 b 的右边。
右：点 P 在向量 AB、BC、CA 同侧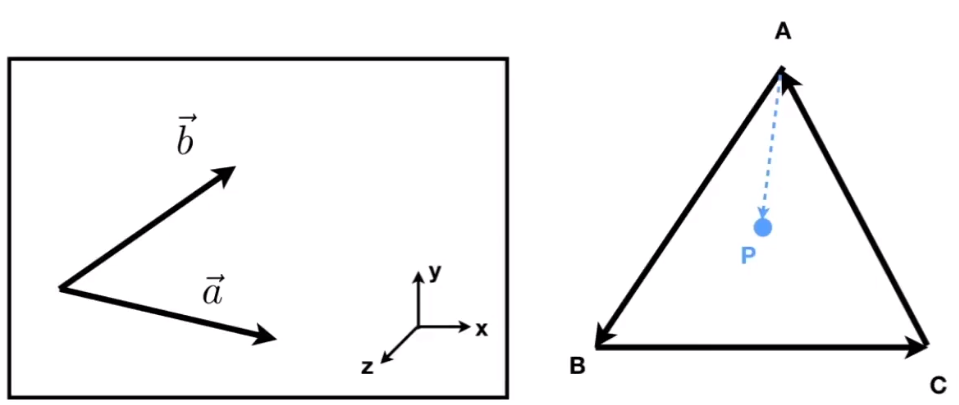
正交坐标系
定义
向量投影
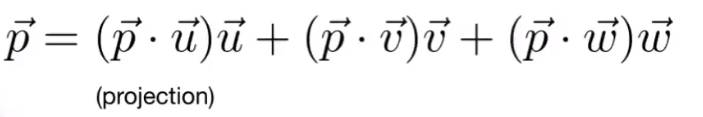
Matrices
矩阵乘法
定义
(M×N)(N×P)=(M×P)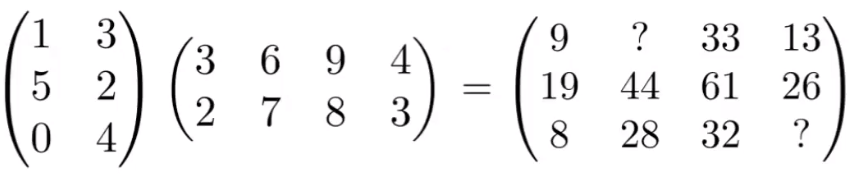
性质
- 无交换律
- 有分配和结合律
转置
单位阵
若有收获，就点个赞吧
0 人点赞
