神经网络可以通过 torch.nn 包来构建。

现在对于自动梯度 (autograd) 有一些了解，神经网络是基于自动梯度 (autograd)来定义一些模型。一个 nn.Module 包括层和一个方法 forward(input) 它会返回输出(output)。

例如，看一下数字图片识别的网络：

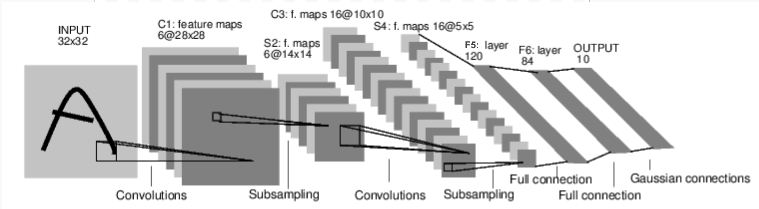
PyTorch 神经网络 - PyTorch官方教程中文版 - 图1

这是一个简单的前馈神经网络，它接收输入，让输入一个接着一个的通过一些层，最后给出输出。

一个典型的神经网络训练过程包括以下几点：

  1. 定义一个包含可训练参数的神经网络

  2. 迭代整个输入

  3. 通过神经网络处理输入

  4. 计算损失 (loss)

  5. 反向传播梯度到神经网络的参数

  6. 更新网络的参数，典型的用一个简单的更新方法：weight = weight - learning_rate *gradient

定义神经网络

  1. import torch
  2. import torch.nn as nn
  3. import torch.nn.functional as F
  5. class Net(nn.Module):
  6.     def __init__(self):
  7.         super(Net,self).__init__()
  8.         self.conv1=nn.Conv2d(1,6,3)
  9.         self.conv2=nn.Conv2d(6,16,3)
  11.         self.fc1=nn.Linear(16*6*6,120)
  12.         self.fc2=nn.Linear(120,84)
  13.         self.fc3=nn.Linear(84,10)
  15.     def forward(self,x):
  16.         x=self.conv1(x)
  17.         x=F.relu(x)
  18.         x=F.max_pool2d(x,(2,2))
  20.         x=self.conv2(x)
  21.         x=F.relu(x)
  22.         x=F.max_pool2d(x,2)
  24.         x = x.view(-1, self.num_flat_features(x))
  25.         x=F.relu(self.fc1(x))
  26.         x=F.relu(self.fc2(x))
  27.         x=self.fc3(x)
  30.     def num_flat_features(self, x):
  31.         size = x.size()[1:]  # all dimensions except the batch dimension
  32.         num_features = 1
  33.         for s in size:
  34.             num_features *= s
  35.         return num_features
  38. net = Net()
  39. print(net)

输出：

  1. Net(
  2.   (conv1): Conv2d(1, 6, kernel_size=(3, 3), stride=(1, 1))
  3.   (conv2): Conv2d(6, 16, kernel_size=(3, 3), stride=(1, 1))
  4.   (fc1): Linear(in_features=576, out_features=120, bias=True)
  5.   (fc2): Linear(in_features=120, out_features=84, bias=True)
  6.   (fc3): Linear(in_features=84, out_features=10, bias=True)
  7. )

你刚定义了一个前馈函数，然后反向传播函数被自动通过 autograd 定义了。你可以使用任何张量操作在前馈函数上。

一个模型可训练的参数可以通过调用 net.parameters() 返回：

  1. params = list(net.parameters())
  2. print(len(params))
  3. print(params[0].size())

输出：

  1. 10
  2. torch.Size([6, 1, 3, 3])

让我们尝试随机生成一个 32x32 的输入。注意：期望的输入维度是 32x32 。为了使用这个网络在 MNIST 数据及上，你需要把数据集中的图片维度修改为 32x32。

  1. input = torch.randn(1, 1, 32, 32)
  2. out = net(input)
  3. print(out)

输出：

  1. tensor([[-0.1546, -0.1180,  0.0092,  0.1134, -0.0810,  0.0199,  0.0303,  0.0010,
  2.          -0.0664,  0.0199]], grad_fn=<AddmmBackward>)

把所有参数梯度缓存器置零，用随机的梯度来反向传播

net.zero_grad()
out.backward(torch.randn(1, 10))

torch.nn only supports mini-batches. The entire torch.nn package only supports inputs that are a mini-batch of samples, and not a single sample.
For example, nn.Conv2d will take in a 4D Tensor of nSamples x nChannels x Height x Width.
If you have a single sample, just use input.unsqueeze(0) to add a fake batch dimension.

Recap:

  • torch.Tensor - A multi-dimensional array with support for autograd operations like backward(). Also holds the gradient w.r.t. the tensor.
  • nn.Module - Neural network module. Convenient way of encapsulating parameters, with helpers for moving them to GPU, exporting, loading, etc.
  • nn.Parameter - A kind of Tensor, that is automatically registered as a parameter when assigned as an attribute to a Module.
  • autograd.Function - Implements forward and backward definitions of an autograd operation. Every Tensor operation creates at least a single Function node that connects to functions that created a Tensor and encodes its history.

损失函数

一个损失函数需要一对输入：模型输出和目标，然后计算一个值来评估输出距离目标有多远。

有一些不同的损失函数在 nn 包中。一个简单的损失函数就是 nn.MSELoss ，这计算了均方误差。

例如：

output = net(input)
target = torch.randn(10)  
target = target.view(1, -1)  
criterion = nn.MSELoss()

loss = criterion(output, target)
print(loss)

输出：

tensor(0.8943, grad_fn=<MseLossBackward>)

现在，如果你跟随损失到反向传播路径，可以使用它的 .grad_fn 属性，你将会看到一个这样的计算图：

input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
      -> view -> linear -> relu -> linear -> relu -> linear
      -> MSELoss
      -> loss

所以，当我们调用 loss.backward()，整个图都会微分，而且所有的在图中的 requires_grad=True 的张量将会让他们的 grad 张量累计梯度。

为了演示，我们将跟随以下步骤来反向传播。

print(loss.grad_fn)  
print(loss.grad_fn.next_functions[0][0])  
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])

输出：

<MseLossBackward object at 0x7fab77615278>
<AddmmBackward object at 0x7fab77615940>
<AccumulateGrad object at 0x7fab77615940>

反向传播

为了实现反向传播损失，我们所有需要做的事情仅仅是使用 loss.backward()。你需要清空现存的梯度，要不然帝都将会和现存的梯度累计到一起。

现在我们调用 loss.backward() ，然后看一下 con1 的偏置项在反向传播之前和之后的变化。

net.zero_grad()     

print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)

loss.backward()

print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)

输出：

conv1.bias.grad before backward
tensor([0., 0., 0., 0., 0., 0.])
conv1.bias.grad after backward
tensor([ 0.0010,  0.0007, -0.0088,  0.0047,  0.0003,  0.0008])

更新神经网络参数

最简单的更新规则就是随机梯度下降。

weight = weight - learning_rate * gradient

我们可以使用 python 来实现这个规则：

learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)

尽管如此，如果你是用神经网络，你想使用不同的更新规则，类似于 SGD, Nesterov-SGD, Adam, RMSProp, 等。为了让这可行，我们建立了一个小包：torch.optim 实现了所有的方法。使用它非常的简单。

import torch.optim as optim

# create your optimizer
optimizer=optim.SGD(net.parameters(),lr=0.01)

# in your training loop:
optimizer.zero_grad() # zero the gradient buffers
output=net(input)
loss=criterion(output,target)
loss.backward()
optimizer.step()  # Does the update

下载 Python 源代码：

neural_networks_tutorial.py

下载 Jupyter 源代码：

neural_networks_tutorial.ipynb
http://www.pytorch123.com/SecondSection/neural_networks/