卷积(convolution)
卷积是通过 Filter 提取原图像的特征,Filter 会随着梯度下降提取出图像的主要特征。如图:
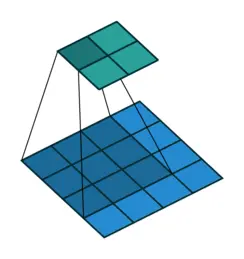
蓝色为原图,深蓝色为 Filter,绿色为提取后的特征
再看看下图卷积是如何进行运算的:
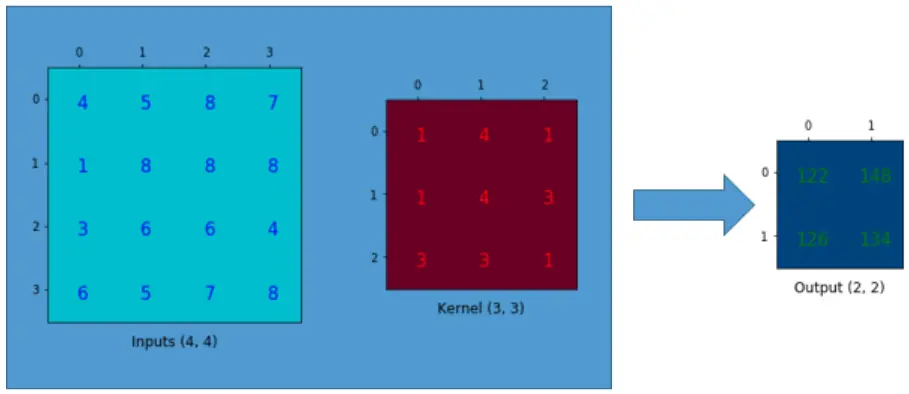
输入,Falter,输出
细节过程:
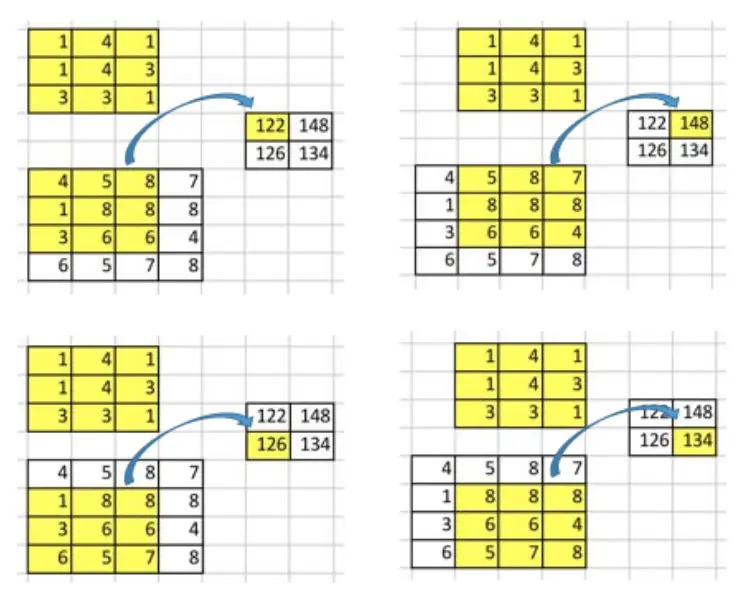
卷积细节操作
卷积操作实质上表示了一种多对一的关系,就如上图所示通过一个 Filter 将 input 中的 9 个 pixel 与 output 中的一个 pixel 相对应。
我们将上述过程用矩阵表示一下
Filter:
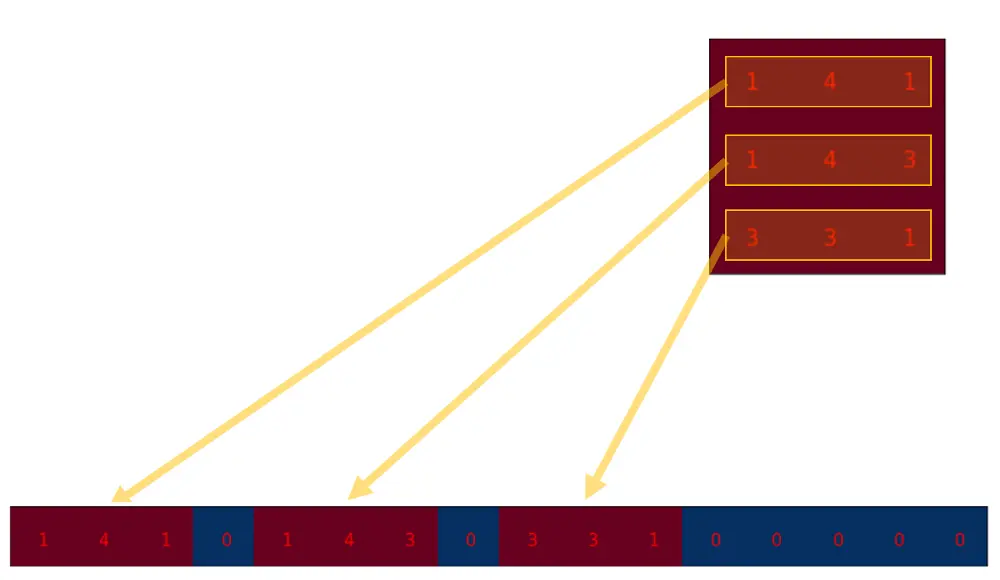
image.png
你可能在想这些蓝色的 0 是怎么来的?看图:
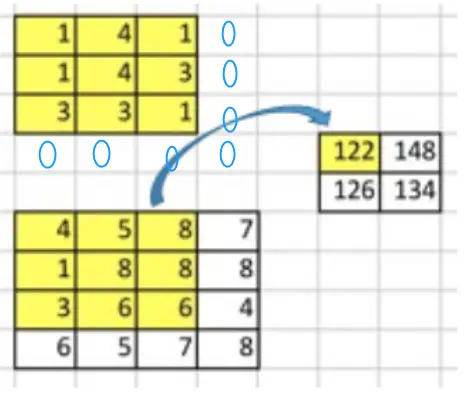
Filter
将上图中的 Filter 进行 flatten 就可以得到

Filter 进行 flatten
我们将 4 次的 3x3 的 Filter 操作用一个 4x16 的矩阵表示:

Convolution Matrix
那么卷积的运算就可以用矩阵表示为:
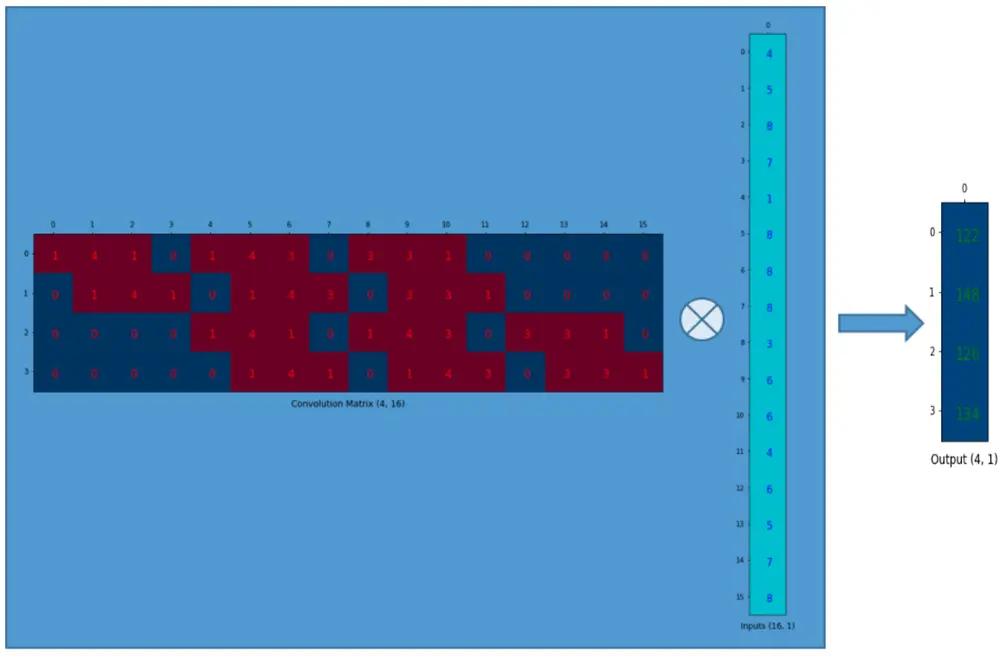
Convolution Matrix operation
将 output reshape 成 2x2 的 matrix

output
其结果和细节过程中的 output 是一样的。接下来我们介绍反卷积。
反卷积(Transposed Convolution)
反卷积,输入图片的特征,输出图片,起到通过特征还原原图的作用。如图:
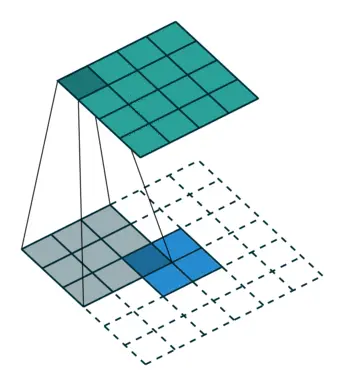
蓝色为提取后的特征,阴影为 Filter,绿色为原图
有了上面的 Convolution Matrix(4x16),我们对它进行 transpose 得到 Transposed Convolution Matrix(16x4)然后进行如下操作:
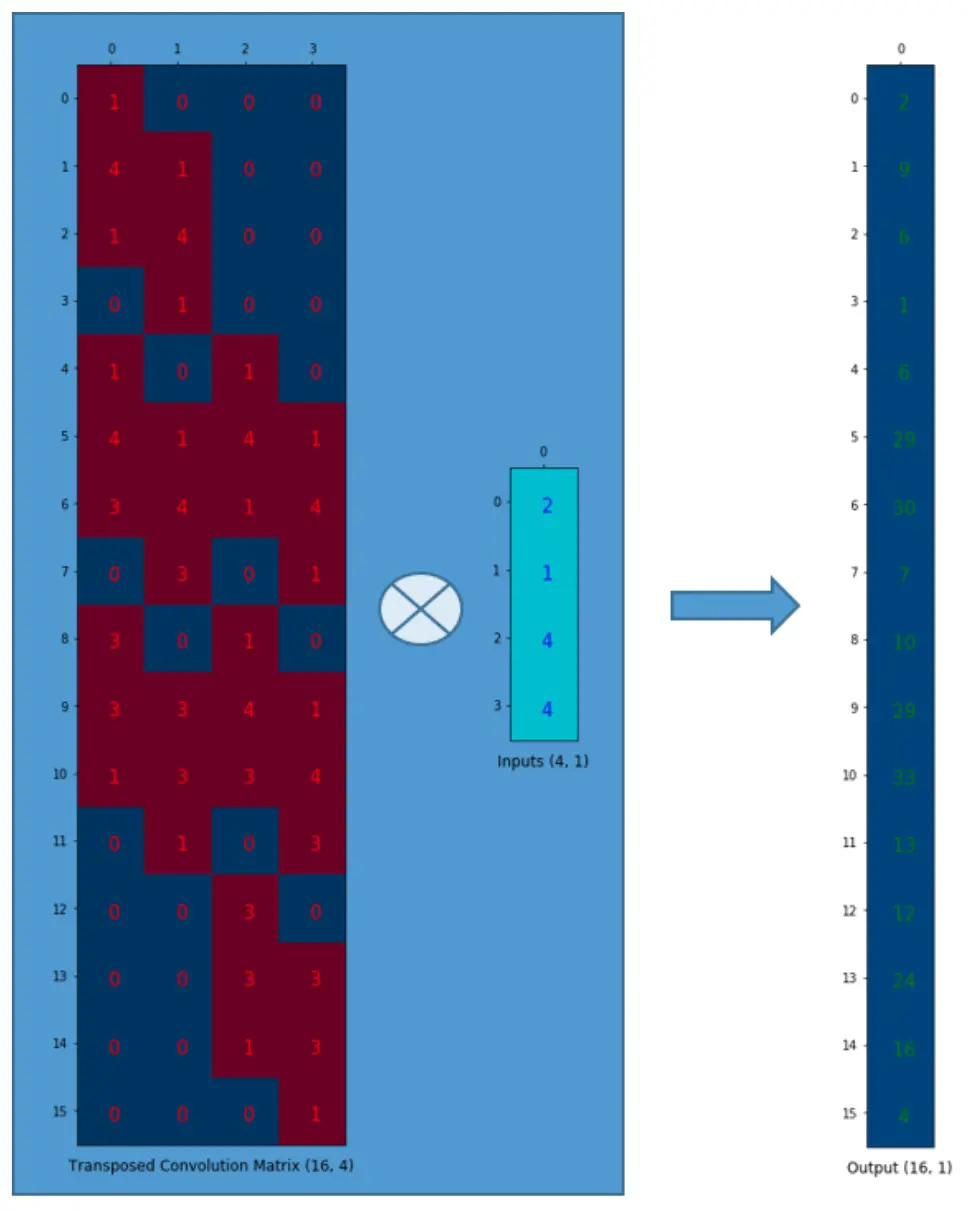
Transposed Convolution Matrix operation
再将反卷积的 output reshape 成 4x4 的矩阵

output
神奇的事情发生了:通过 Transposed Convolution Matrix 的矩阵乘法,我们将 input 的特征转变成了与原图类似结构的图像。这样一来只要我们通过训练去调整 Transposed Convolution Matrix 中的 weight,就可以通过特征尽可能的还原原图。
反卷积操作实质上表示了一种一对多的关系,就如上图所示通过一个 Filter 将 output 中的 1 个 pixel 与 input 中的 9 个 pixel 相对应。
](https://www.jianshu.com/p/3eff28f8d771)

