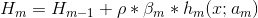- 介绍一下Boosting的思想?
- 最小二乘回归树的切分过程是怎么样的?
- 有哪些直接利用了Boosting思想的树模型?
- gbdt和boostingtree的boosting分别体现在哪里?
- gbdt的中的tree是什么tree?有什么特征?
- 常用回归问题的损失函数?
- 常用分类问题的损失函数?
- 什么是gbdt中的损失函数的负梯度?
- 如何用损失函数的负梯度实现gbdt?
- 拟合损失函数的负梯度为什么是可行的?
- 即便拟合损失函数负梯度是可行的,为什么不直接拟合残差? 拟合负梯度好在哪里?
- Shrinkage收缩的作用?
- feature属性会被重复多次使用么?
- gbdt如何进行正则化的?
- 为什么集成算法大多使用树类模型作为基学习器?或者说,为什么集成学习可以在树类模型上取得成功?
- gbdt的优缺点?
- gbdt和randomforest区别?
- GBDT和LR的差异?
介绍一下Boosting的思想?
- 初始化训练一个弱学习器,初始化下的各条样本的权重一致
- 根据上一个弱学习器的结果,调整权重,使得错分的样本的权重变得更高
- 基于调整后的样本及样本权重训练下一个弱学习器
-
最小二乘回归树的切分过程是怎么样的?
回归树在每个切分后的结点上都会有一个预测值,这个预测值就是结点上所有值的均值
- 分枝时遍历所有的属性进行二叉划分,挑选使平方误差最小的划分属性作为本节点的划分属性
- 属性上有多个值,则需要遍历所有可能的属性值,挑选使平方误差最小的划分属性值作为本属性的划分值
-
有哪些直接利用了Boosting思想的树模型?
gbdt和boostingtree的boosting分别体现在哪里?
boostingtree利用基模型学习器,拟合的是mse(回归)或者指数损失函数(分类)
gbdt利用基模型学习器,拟合的是当前模型与标签值的损失函数的负梯度
gbdt的中的tree是什么tree?有什么特征?
常用回归问题的损失函数?
mse:
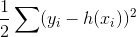
- 负梯度:y-h(x)
- 初始模型F0由目标变量的平均值给出
- 绝对损失:
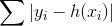
- 负梯度:sign(y-h(x))
- 初始模型F0由目标变量的中值给出
Huber损失:mse和绝对损失的结合
对数似然损失函数
- 二元且标签y属于{-1,+1}:𝐿(𝑦,𝑓(𝑥))=𝑙𝑜𝑔(1+𝑒𝑥𝑝(−𝑦𝑓(𝑥)))
- 负梯度:y/(1+𝑒𝑥𝑝(−𝑦𝑓(𝑥)))
- 多元:
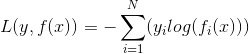
- 二元且标签y属于{-1,+1}:𝐿(𝑦,𝑓(𝑥))=𝑙𝑜𝑔(1+𝑒𝑥𝑝(−𝑦𝑓(𝑥)))
指数损失函数:𝐿(𝑦,𝑓(𝑥))=𝑒𝑥𝑝(−𝑦𝑓(𝑥))
利用
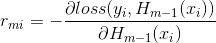 可以计算得到x对应的损失函数的负梯度
可以计算得到x对应的损失函数的负梯度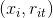 ,据此我们可以构造出第t棵回归树,其对应的叶子结点区域
,据此我们可以构造出第t棵回归树,其对应的叶子结点区域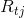 j为叶子结点位置
j为叶子结点位置- 构建回归树的过程中,需要考虑找到特征A中最合适的切分点,使得切分后的数据集D1和D2的均方误差最小
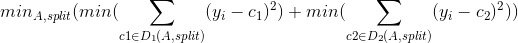
- 针对每一个叶子节点里的样本,我们求出使损失函数最小,也就是拟合叶子节点最好的输出值𝑐𝑡𝑗,
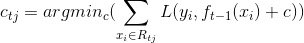
- 首先,根据feature切分后的损失均方差大小,选取最优的特征切分
- 其次,根据选定的feature切分后的叶子结点数据集,选取最使损失函数最小,也就是拟合叶子节点最好的输出值
- 这样就完整的构造出一棵树:
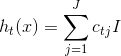
-
拟合损失函数的负梯度为什么是可行的?
泰勒展开的一阶形式:
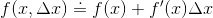
- m轮树模型可以写成:
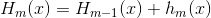
- 对
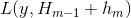 进行泰勒展开:
进行泰勒展开: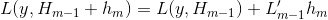 ,其中m-1轮对残差梯度为
,其中m-1轮对残差梯度为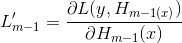
- 对
-
即便拟合损失函数负梯度是可行的,为什么不直接拟合残差? 拟合负梯度好在哪里?
前者不用残差的负梯度而是使用残差,是全局最优值,后者使用的是 局部最优方向(负梯度)*步长(𝛽)
依赖残差进行优化,损失函数一般固定为反映残差的均方差损失函数,因此 当均方差损失函数失效(该损失函数对异常值敏感)的时候,换了其他一般的损失函数,便很难得到优化的结果。同时,因为损失函数的问题,Boosting Tree也很难处理回归之外问题。 而后者使用梯度下降的方法,对于任意可以求导的损失函数它都可以处理
Shrinkage收缩的作用?
每次走一小步逐渐逼近结果的效果,要比每次迈一大步很快逼近结果的方式更容易得到精确值,即它不完全信任每一棵残差树,认为每棵树只学到了真理的一部分累加的时候只累加了一小部分多学几棵树来弥补不足。 这个技巧类似于梯度下降里的学习率
原始:
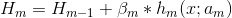
-
feature属性会被重复多次使用么?
会,同时因为特征会进行多次使用,特征用的越多,则该特征的重要性越大
gbdt如何进行正则化的?
子采样
- 每一棵树基于原始原本的一个子集进行训练
- rf是有放回采样,gbdt是无放回采样
- 特征子采样可以来控制模型整体的方差
- 利用Shrinkage收缩,控制每一棵子树的贡献度
-
为什么集成算法大多使用树类模型作为基学习器?或者说,为什么集成学习可以在树类模型上取得成功?
对数据的要求比较低,不需要强假设,不需要数据预处理,连续离散都可以,缺失值也能接受
- bagging,关注于提升分类器的泛化能力
-
gbdt的优缺点?
优点:
数据要求比较低,不需要前提假设,能处理缺失值,连续值,离散值
- 使用一些健壮的损失函数,对异常值的鲁棒性非常强
- 调参相对较简单
缺点:
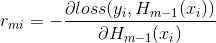
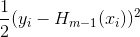 ,gbdt中的残差的负梯度的结果y-H(x)正好与boostingtree的拟合残差一致
,gbdt中的残差的负梯度的结果y-H(x)正好与boostingtree的拟合残差一致
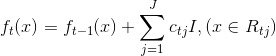
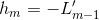 ,所以
,所以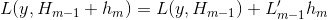 内会让损失向下降对方向前进
内会让损失向下降对方向前进