只要你自己试试模拟随机现象几次，就会加强对概率的了解，比读很多页的数理统计和概率论的文章还有用。学习模拟，不仅是为了解模拟本身，也是为更了解概率而了解模拟。

1 伪随机数

生成（0，1）之间均匀分布的伪随机数的函数为 uniform()

  1. di uniform()
  2. di uniform()
  3. di uniform()

每次都得到一个大于零小于 1 的随机数。
如果要生成一位数的随机数（即 0，1，2，3，4，5，6，7，8，9），可以取小数点后第一位数，通常用下面的命令
di int(10uniform())
两位随机数(0-99)则取小数点后两位小数，即
di int(100uniform())
任意均匀分布随机数（a,b）由下述函数得到
a+(b-a)uniform()
任意均匀分布整数随机数（a,b）由下述函数得到
a+int((b-a)uniform())
也可以同时生成多个随机数，然后将该随机数赋给某个变量。要注意的是，电脑中给出的随机数不是真正的随机数，而是伪随机数，因为它是按照一定的规律生成的。如果给定基于生成伪随机数的初始数值（即 set seed #），则对相同的初始数值，生成的伪随机数序列完
全一样。

  1. clear
  2. set obs 10
  3. gen x1=uniform()
  4. gen x2=uniform() //注意到 x1 与 x2 不一样
  5. set seed 1234
  6. gen y1=uniform()
  7. set seed 1234
  8. gen y2=uniform()
  9. gen y3=uniform() //注意到 y1 与 y2 一样，但均与 y3 不同
  10. set seed 5634
  11. gen z1=uniform()
  12. set seed 1234
  13. gen z2=uniform() //注意到 z2 与 y1,y2 一样，但 z1 与 z2 不同
  14. list

可以从 STATA 上下载专门用于生成服从若干主要分布的随机数生成命令。

  1. search rnd, net
  2. rndbin 1000 0.5 1 //生成 1000 个 0-1 分布，取 1 的概率为 0.5(抛均匀的硬币)

2 简单模拟

利用随机数字表或者电脑软件中的随机数字，来模仿机遇现象，叫模拟（simulation）、一旦有了可靠的概率模型，模拟是找出复杂事件发生概率的有效工具。一个事件在重复结果中发生的比例，迟早会接近它的概率，所以模拟可以对概率做适当的估计。
例 1：如何执行模拟
掷一枚硬币 10 次，结果中会出现至少 3 个连续正面或者至少 3 个连续反面的概率是多少？
思考：
（1） 猜想这个概率大约是多少？
（2） 如何从理论上计算出这个概率？
（3） 如何模拟计算这个概率？
第一步：提出概率模型。
z 每一次掷，正面和反面的概率各为 0.5
z 投掷之间，彼此是独立的。也就是说，知道某一次掷出的结果，不会改变任何其他次所
掷结果的概率。
第二步：分配随机数字以代表不同的结果。
z 随机数字表中的 0-9 每个数字出现的概率都是 0.1
z 每个数字模拟掷一次硬币的结果。
z 奇数代表正面，偶数代表反面。
第三步：模拟多次重复。
z 生成 10 个随机数字
z 记录开心的事件（至少连续三个正面或反面）是否发生，如果发生，记为 1，否则为 0
z 重复 10 次（或者 100，1000，1000000 次），计算概率=开心事件发生/总重复次数。

  1. capt prog drop seq3 
  2. prog seq3,rclass //rclass 选项表示计算结果将由 return 返回到 r() 
  3. drop _all //清空所有数据，不能用 clear 
  4. set obs 10 //将生成 10 个观察值 
  5. tempvar x y z //设定 x,y,z 为临时变量 
  6. gen `x'=int(10*uniform()) //产生 10 个随机变量，可能为 0，1，…，9 
  7. gen `y'=(mod(`x',2)==0) //如果生成的随机变量为奇数，则 y=0;为偶数，y=1 
  8. gen `z'=0 //生成 Z=0 
  9. forvalues i=3/10 { 
  10. replace `z'=1 if `y'==`y'[_n-1] & `y'==`y'[_n-2] in `i' //连续三个变量相等时 z=1 
  11. } 
  12. sum `z'
  13. return scalar max=r(max) //z 取 1 表示高兴的事发生（三连续），否则失败
  14. end
  15. simulate max=r(max),reps(10000) nodots:seq3 //重复 1 万次，取平均结果 
  16. sum

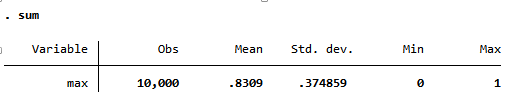
image.png
另一种更简单，但不尽规范的程序是：

  1. clear 
  2. set obs 10 //将生成 10 个观察值 
  3. gen y=0 
  4. gen z=0 
  5. capt prog drop seq3
  6. prog seq3 
  7. replace y=uniform()>0.5 //如果生成的随机变量为奇数，则 y=0;为偶数，y=1
  8. replace z=0 
  9. forvalues i=3/10 { 
  10. replace z=1 if y==y[_n-1] & y==y[_n-2] in `i' 
  11. } 
  12. sum z 
  13. end 
  14. simulate r(max),reps(10000) nodots:seq3 //重复 1 万次，取平均结果 
  15. sum

image.png
由于上述命令要不停生成变量，进行变量代换，所以计算速度较慢，如果使用矩阵，则
计算速度会大大加快，命令也更简捷。

  1. capt prog drop seq3 
  2. program seq3 
  3. drop _all //清空所有数据，不能用 clear 
  4. rndbin 10 0.5 1 
  5. gen z=0 //生成 Z=0 
  6. forvalues i=3/10 { 
  7. replace z=1 if xb==xb[_n-1] & xb==xb[_n-2] in `i' //连续三个变量相等时 z=1 
  8. } 
  9. sum z 
  10. end 
  11. simulate max=r(max),reps(10000) nodots:seq3 //重复 1 万次，取平均结果 
  12. sum
  13. 另一种形式：
  14. mata 
  15. A=uniform(10000,10):>0.5 //每行为一次试验, 每列为某次试验中硬币的正反面结果
  16. B=J(10000,1,0) //记录每次试验的结果,先记为 0. 若高兴结果出现再改为 1
  17. for (j=1;j<=rows(A);j++) { //第 j 次试验
  18. for (i=3;i<=cols(A);i++) { //第 j 次试验中第 i 次硬币出现结果
  19. if ( A[j,(i-2,i-1,i)]==(0,0,0) | A[j,(i-2,i-1,i)]==(1,1,1) ) {
  20. B[j,1]=1 //若连续为正面或者连续为反面,则记为 1
  21. break 
  22. } 
  23. } 
  24. } 
  25. mean(B) //求开心事件的次数
  26. end

3 复杂模拟

例 2：我们要女儿
任务：一对夫妇计划生孩子生到有女儿才停，或者生了三个就停，他们拥有女儿的概率
是多大？
思考：理论上，概率是多少？
第一步：概率模型
每一个孩子是女孩的概率是0.49，且各个孩子的性别是互相独立的。
第二步：分配数字
00，01，02，。。。，49=女孩
49，50，51，。。。，99=男孩
第三步：模拟
从随机数表中生成一对一对的数字，直到有了女儿，或已有3个孩子。
重复100次。
6905 16 48 17 8717 648987
男女 女 女 女 男女 男男男
用数学可以计算出来，有女孩的真正概率是0.867

  1. capt program drop girl
  2. program girl, rclass
  3. drop _all
  4. set obs 3
  5. gen x=int(100*uniform())
  6. gen y=(x<49) //生女孩 y=1,生男孩，y=0
  7. sum y
  8. return scalar max=r(max) //若至少有一个女孩，则 max 取 1，若三个全为男孩，取 0
  9. end
  10. simulate max=r(max),reps(10000) nodots:girl
  11. sum

另一种办法

  1. clear
  2. set obs 3
  3. gen y=0
  4. capt program drop girl
  5. program girl
  6. replace y=(int(100*uniform())<49) //生女孩 y=1,生男孩，y=0
  7. sort y
  8. scalar girl=y[_N] //若至少有一个女孩，则 girl 取 1，若三个全为男孩，取 0
  9. end
  10. simulate girl, reps(10000) nodots:girl
  11. sum

更快的模拟方式.

  1. capt program drop girl 
  2. program girl 
  3. mat A=matuniform(1,3)
  4. scalar girl=1
  5.  if A[1,1]>0.49 & A[1,2]>0.49 & A[1,3]>0.49 { 
  6. scalar girl=0 //若三个全为男孩，生女孩数为 0 
  7. } 
  8. end 
  9. simulate girl,reps(10000) nodots:girl 
  10. tab _sim
  1. mata 
  2. A=uniform(10000,3):<0.49 
  3. B=J(10000,1,1) 
  4. for (i=1;i<=rows(A);i++) { 
  5. if (A[i,.]==(0,0,0)) { 
  6. B[i,1]=0 //若三个全为男孩，生女孩数为 0
  7. } 
  8. } 
  9. mean(B) 
  11. end

4 多阶段模拟

张三肾脏不行了，正在等待换肾，他的医师提供了和他情况类似的病人资料。“换肾后的五年存活率：撑过手术的有0.9，术后存活的人中有0.6移植成功，0.4还得回去洗肾；五年后，有新肾的人70%仍然活着，而洗肾的只有一半仍活着。”张三希望知道，他能活过五年的概率，然后再决定是否换肾。

  1. capt program drop surv 
  2. program surv 
  3. scalar z=1 
  4. if uniform()<0.1 { 
  5. scalar z=0 
  6. } 
  7. else { 
  8. if uniform()<0.6 { 
  9. if uniform()>=0.7 { 
  10. scalar z=0 
  11. } 
  12. } 
  13. else { 
  14. if uniform()>=0.5 { 
  15. scalar z=0 
  16. } 
  17. } 
  18. } 
  19. end 
  20. simulate z,reps(10000) nodots:surv 
  21. sum