1 二项分布

Binomial(n,k,p)计算成功概率为 p 的随机事件，在 n 次独立重复试验中，成功次数大于等于 k 次的概率。如出现概率为 0.6 的某随机现象，在六次独立重复试验中，出现 4 次及以上的概率为.54432。
di Binomial(6,4,0.6)
.54432
如果要计算出，恰好成功 4 次的概率，则需要按如下方式求得
di Binomial(6,4,0.6)- Binomial(6,5,0.6)
.27648
掷一枚硬币二次，出现一次正面的概率为
di Binomial(2,1,0.5)-Binomial(2,2,0.5)
0.5
掷一枚硬币二次，至少出现一次正面的概率为
di Binomial(2,1,0.5)
.75
掷一枚硬币二次，出现两次正面的概率为
di Binomial(2,2,0.5)
.25
掷一枚硬币二次，不出现或者出现正面的概率为
di Binomial(2,0,0.5)
1

2 标准正态分布函数

在标准正态分布中，出现小于-1.96 的随机数的概率是 0.025
di normal(-1.96)
.0249979
而出现小于 1.96 的随机数的概率为 0.975
di normal(1.96)
.9750021
大于 1.96 的随机数出现的概率则为
di 1-normal(1.96)
.0249979
标准正态分布函数的图示

twoway function y=normal(x), rang(-4 4)

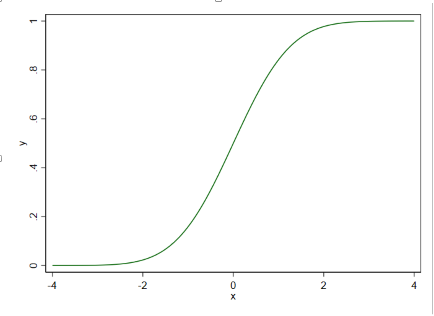
任务：利用计算机得到标准正态分布概率表

mat z=J(61,11,.)
forvalues i=1/61{
mat z[i',1]=(i'-31 )/10
forvalues j=2/11 {
mat z[i',j']=normal((i'-31)/10+(j'-2)/100)
}
}
matrix colnames z = z 0 1 2 3 4 5 6 7 8 9
mat list z, format(%5.4f)

3 正态分布函数及其反函数

一般的正态分布函数，可以根据公式(x-m)/s=z来变形得到
例：人的智商（I.Q.）得分一般服从均值为 100，标准差为 16 的正态分布，随机抽取一人，他的智商在 100-115 之间的概率是多少？（以频率为表述，即智商在100-115 之间的人占多大比例？）
di normal((115-100)/16)- normal((100-100)/16)
.32574929
正态分布函数的图示

twoway function y=normal((x-100)/16), rang(50 150)

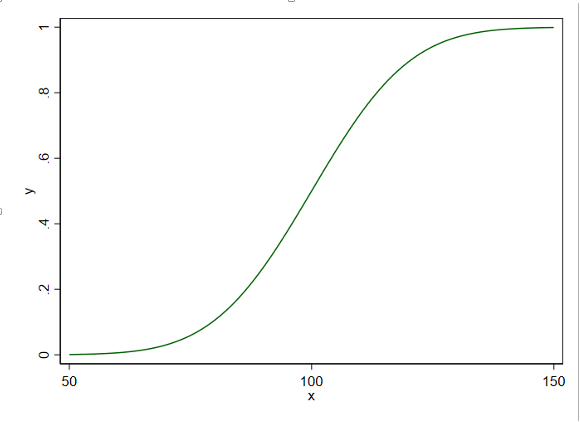
求标准正态分布累积函数值为 0.975 的点对应的随机数
di invnormal(.975)
1.959964
结果为 1.96，正好与 normal(1.96)相对应，他们互为反函数。类似地计算
. di invnormal(.995)
2.5758293
例：设在注册会计师的会计科目考试中，其通过率只有 10%，从历年的经验来看，分数的均值和标准差分别为 72 和 13。如果分数近似正态分布，为了获得顶部 10%的分数并通过考试所需要的最小分数是多少？
di invnormal(0.9)*13+72
88.66017

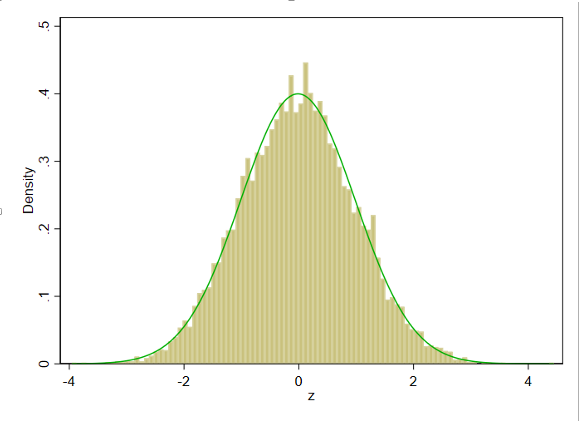
4 服从正态分布的随机数

定理：设X是一个连续型随机变量，其分布函数F（x）是严格单调递增的，则Y=F（X）服从[0，1]上的均匀分布。

clear
set obs 10000
gen z=invnormal(uniform()) //得到服从标准正态分布的随机数
hist z,bin(100) norm //画出直方图并配上标准正态分布曲线

5 正态分布密度函数

STATA 提供了三种计算正态密度函数的命令，分别是标准正态密度函数
di normalden(1.95)
.05959471
均值为零，标准差为 s 的正态密度函数，经换算，与标准正态密度函数等价
normalden(z,s) = normalden(z)/s
di normalden(1.95,10)
.00595947
均值为 m,标准差为 s 的正态密度函数，经换算，与标准正态密度函数等价
normalden(x,m,s) = normalden((x-m)/s)/s
di normalden(29.5,10,10)

6 分位数

分位数是统计分布的一类数字特征。
定义：设随机变量 X 的分布函数 F（x），对给定的实数α（0<α<1），如果实数Fα满足：
P{X>Fα}=α,即 1-F（ Fα）=α，或者 F（ Fα）=1-α 则称为随机变量 X 的分布的水平α的上侧分位数。或分布函数 F（x）的水平α
的上侧分位数。Fα=invF(1-α)

#delimit ;
twoway
function y=0.975, rang(-4 1.96) dropline(1.959)||
function y=normal(x), range(-4 4) clstyle(foreground) ||,
legend(off)
xlabel(1.96)
ylabel(.975)
;
#delimit cr

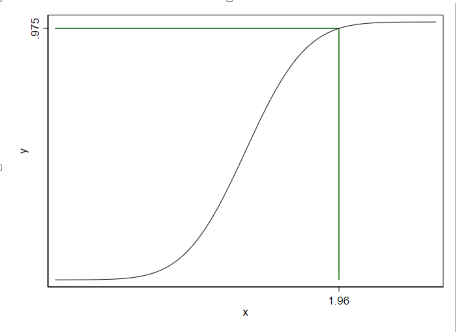
标准正态分布的水平α=0.05 的上侧分位数为
di invnormal(0.95)
1.6448536
标准正态分布的水平α=0.05 的双侧分位数为
di invnorm(0.975)
1.959964

7 卡方分布

卡方分布：设 X1，X2，。。。，Xn是 n 个相互独立的随机变量，且 Xi均服从标准正态分布，则 X=Σxi^2服从自由度为 n 的卡方分布。

#delimit;
tw function y=(chi2(2,x)-chi2(2,(x-0.01)))/0.01,rang(0 30) ||
function y=(chi2(4,x)-chi2(4,(x-0.01)))/0.01,rang(0 30) ||
function y=(chi2(8,x)-chi2(8,(x-0.01)))/0.01,rang(0 30) ,legend(off);
tw function y=chi2(2,x),rang(0 30) ||
function y=chi2(4,x),rang(0 30) ||
function y=chi2(8,x),rang(0 30), legend(off);
***非中心化卡方分布图
tw function y=100*(chi2(2,x)-chi2(2,(x-0.01))),rang(0 30) ||
function y=100*(nchi2(2,4,x)-nchi2(2,4,(x-0.01))),rang(0 30) ||
function y=100*(nchi2(2,8,x)-nchi2(2,8,(x-0.01))),rang(0 30) ,legend(off);

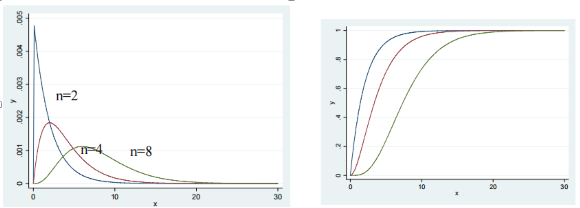
自由度为10时，累积分布为0.95所对应的随机变量为，即10个独立的标准正态分布随机变量平方和小于18.31的可能性为0.95.
di invchi2(10,0.95)
18.307038
di chi2(10,18.31)
.95004583
卡方分布的分位数函数与累积分布函数的关系是chi2(n,x)=1- chi2tail(n,x)
di chi2tail(10,18.31)
.04995417
卡方分布的分位数的反函数与其累积分布的反函数的关系是invchi2(n,p)=
invchi2tail(n,1-p)
di invchi2tail(10,0.05)
18.307038
任务：自己做出卡方分布的临界值

mat X=J(31,3,.)
forvalues n=1/30{
mat X[n',1]=invchi2tail(n',0.1)
mat X[n',2]=invchi2tail(n',0.05)
mat X[n',3]=invchi2tail(n',0.01)
}
mat list X, format(%5.2f)

8 t 分布的分位数

t 分布是标准正态分布与自由度为 n 的卡方分布的函数
自由度为 8 的 t 分布的水平 0.05 的上侧分位数为
di invttail(8,0.05)
1.859548
即
di ttail(8,1.86)
.04996531
由于 t 分布为对称分布，因此双侧分位数为
di invttail(8,0.025)
2.3060041
di ttail(8,2.306)
.02500016
任务：自己做出 t 分布表

mat t=J(31,5,.)
forvalues n=1/30{
mat t[n',1]=invttail(n',0.1)
mat t[n',2]=invttail(n',0.05)
mat t[n',3]=invttail(n',0.025)
mat t[n',4]=invttail(n',0.01)
mat t[n',5]=invttail(n',0.005)
}
mat list t, format(%5.3f)

9 F 分布

F 分布是两个卡方分布的均商（自由度平均）

#delimit ;
twoway
function y=Fden(2,8,x), rang(0 4) ||
function y= Fden(6,8,x), rang(0 4) ||
function y= Fden(6,20,x), rang(0 4) legend(off);

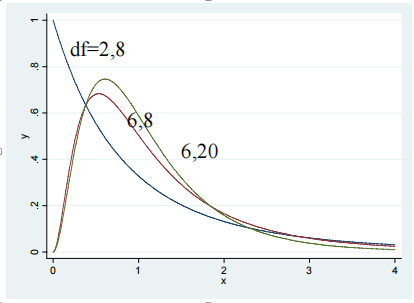
设 X 服从分子自由度为 10，分母自由度为 5 的 F 分布，求 X 小于 4.74 的概率
di F(10,5,4.74)
.95010421
di invF(10,5,0.95)
4.7350631
di Ftail(10,5,4.74)
.04989579
di invFtail(10,5,0.05)
4.7350631
设 X 服从分子自由度为 5，分母自由度为 10 的 F 分布，求 X 小于的概率
. di F(5,10,3.326)
.95000672
. di invF(5,10,0.95)
3.3258345
. di Ftail(5,10,3.326)
.04999328
. di invFtail(5,10,0.05)
3.3258345
可见，F 分布的累积分布函数与分位数的关系为
F(n,m,f)=1-Ftail(n,m,f)
反函数之间的关系为
invF(n,m,p)=invFtail(n,m,1-p)
交换第一自由度与第二自由度，则两个分数之间的关系为
Ftail(m,n,a)= 1/ [Ftail(n,m,1a)]
di invFtail(5,10,0.05)
3.3258345
di 1/(invFtail(10,5,0.95))
3.3258345
任务：自己做出 F 分布表(p756)

mat F=J(21,11,.)
forvalues i=1/21{
mat F[i',1]=i'+9
forvalues j=2/11 {
mat F[i',j']=invFtail((j'-1),(i'+9),0.05)
}
}
matrix colnames z = F 1 2 3 4 5 6 7 8 9 10
mat list F, format(%4.2f)

320-语言类

【stata-12】分布函数