用 MATA 可以完成除绘图以外的所有 STATA 数据处理和分析功能。这里介绍的仍然是传统的 STATA 矩阵命令。

1 生成矩阵

1 输入新矩阵

\ 表示换行，其它运算正常使用。
可以直接录入一个新的矩阵

  1. matrix A= (1,0,1\2,1,0\-3,2,-5) //录入矩阵 A
  2. matrix list A //显示录入的矩阵 A 
  3. matlist A //显示录入的矩阵 A,该命令只能在 stata9 以上版本使用
  4. matrx B=(1+1,2*3/4 \ 5/2, 3^2) 
  5. matrix list B 
  6. matrix C=(2,3,4) 
  7. matrix E=(1\2\3) 
  8. matrix F=(4) 
  9. matrix rownames A= sex edu marriage 
  10. matrix colnames A=obs1 obs2 obs3 
  11. matrix list

2 生成特定格式矩阵

生成一个 5 行 3 列的矩阵 A，矩阵中的元素均为 0 

  1. matrix A=J(5,3,0)

生成一个 6 阶单位阵 I 

  1. matrix I=I(6)

生成一个 3 行 5 列的随机矩阵 R，每个随机元素均服从（0，1）均匀分布

  1. matrix R=matuniform(3,5) 
  2. matrix d=(1,4,9) 
  3. matrix D=diag(d) //以d中元素为对角元素生成对角矩阵D 
  4. matrix list D

3 数据与矩阵之间的相互转化

将矩阵 R 转换为数据文件
mkmat varlist [if exp] [in range] [matrix(matname) nomissing ]
svmat [type] A [names(col|eqcol|matcol|string) ]
matname A namelist [rows(range) columns(range) explicit ]

  1. sysuse auto, clear 
  2. *将 foreign weight displ 这三个变量的前 5 个观察数据转换为矩阵 X 
  3. mkmat foreign weight displ in 1/5, matrix(X) 
  4. matrix list X *将带条件的数据转换为矩阵 Y 
  5. mkmat foreign weight displ if fore==1, matrix(Y) 
  6. matrix list Y 
  7. matrix A= (1,0,1\2,1,0\-3,2,-5) //录入矩阵 A
  8. svmat A //将矩阵 A 中的数据转化为数据，变量为 A1，A2，A3 
  9. list 
  10. svmat A, name(ccb) //将矩阵 A 中的数据转化为新的变量 ccb1，ccb2，ccb3

2 矩阵四则运算

image.png

1 矩阵扩展

  1. matrix A= (1,0,1\2,1,0\-3,2,-5) 
  2. matrix B=(4\3\7) 
  3. matrix C=(A,B) 
  4. matrix list C
  5. matrix D= (10,9,25) 
  6. matrix E= (A\D) 
  7. matrix list E

2 矩阵加、减、数乘、除法

  1. mat e=(3,5\2,0)
  2. mat t=(1,3\2,1)
  3. mat r1=e+t //加
  4. mat list r1
  5. mat r2=e-t //减
  6. mat list r2
  7. mat e2=2*e //数乘（每个元素均乘标量）
  8. mat list e2
  9. mat e3=e/10 //除法（每个元素均除以一个标量）
  10. mat list e3

3 矩阵乘法、直乘及 Kronecker 乘积运算

  1. mat w=e*t //乘，数学种的矩阵相乘
  2. mat list w 
  3. *矩阵乘法不满足交换律，一般来说 a*b~=b*a 
  4. mat a=(2,3\1,-2\3,1) 
  5. mat b=(1,-2,-3\2,-1,0) 
  6. mat ab=a*b
  7. mat list ab 
  8. mat ba=b*a 
  9. mat list ba 
  10. /*两个矩阵对应元素直接相乘，要求两个矩阵结构相同。*/
  11. mat A=(1,2\3,4\5,6) 
  12. mat B=(7,8\9,0\1,9) 
  13. matrix H=hadamard(A,B) 
  14. mat list H

/矩阵的 Kronecker 乘积运算定义如下：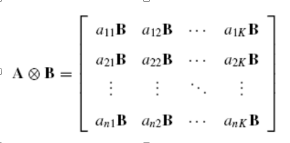
image.png
Kronecker 乘积运算对 A 和 B 没有任何要求。/ 

  1. mat ab2=a#b 
  2. mat list ab2 
  3. mat ba2=b#a 
  4. mat list ba2

3 矩阵函数

image.png
以上表格引用自arlion《Estimation with STATA－Matrix》

1 转置、求迹

  1. mat b=(1,-2,-3\2,-1,0) 
  2. mat list b
  3. mat b2=b` //b2 为 b 的转置矩阵
  4. mat list b2
  5. /*迹的表达式为，它只能对方阵求，其结果是一个数 */ 
  6. matrix A= (1,0,1\2,1,0\-3,2,-5) 
  7. scalar a=trace(A) //求 A 的主对角线上的元素之和并赋予该值给 b 
  8. scalar list

2 求逆、求行列式的值

  1. matrix B=inv(A) //B 为 A 的逆矩阵
  2. mat list B
  3. /*任务：解线性方程 Ax=b，其中： 
  4. A=(1,-1,1,-2\2,0,-1,4\3,2,1,0\-1,2,-1,2)
  5. b=(2\4\-1\-4) */
  6. mat A1=(1,-1,1,-2\2,0,-1,4\3,2,1,0\-1,2,-1,2) 
  7. mat b=(2\4\-1\-4)
  8. matrix B1=inv(A1) //B 为 A 的逆矩阵
  9. mat X=B1*b 
  10. mat list X 
  11. mat a=(1,0,1\2,1,0\-3,2,-5) 
  12. scalar aa=det(a) //det()计算行列式的值
  13. mat d=(1,-1,1,-2,2\2,0,-1,4,4\3,2,1,0,-1\-1,2,-1,2,-4) 
  14. mat dd=det(d) 
  15. scalar list

3 返回或者修改矩阵中某个元素的值

  1. el(A,i,j)=A[i,j]
  3. mat d=(1,-1,1,-2,2\2,100,-1,4,4\3,2,1,0,-1\-1,2,-1,2,-4) 
  4. mat list d
  5. scalar dd=d[2,2]
  6. scalar ddd=el(d,2,2) 
  7. scalar list 
  8. mat d[1,3]=1000 
  9. mat list d

4 Nullmat 命令

该命令在编程时特别有用，有点类似于数据管理中的 mereg 命令

  1. mat A=I(3)
  2. mat B=J(3,3,9)
  3. mat list C //矩阵C不存在
  4. mat C=(nullmat(C),A) //当C矩阵不存在时，将得到C=A 
  5. mat list C //C=A 
  6. mat C=(nullmat(B),A) //C变成由B和A两个矩阵横向对接
  7. mat list C //C=（B，A）
  8. mat A=A/10 
  9. mat C=(nullmat(C),A) //C在原来的基础上对接了A变成新的矩阵
  10. mat list C //C=（C，A）

5 其他矩阵函数

  1. matrix A= (1,0,1\2,1,0\-3,2,-5) 
  2. matrix e=vec(A) //将矩阵A转化为一维列矩阵e 
  3. mat list e
  4. matrix d=vecdiag(A) //返回矩阵A的对角元素为一行向量d 
  5. matrix list d
  7. mat J=J(10,2,.) 
  8. scalar a=rowsof(J) //求矩阵的行数
  9. scalar b=colsof(J) //求矩阵的列数
  10. scalar list