数据结构-树

孩子兄弟表示法

这种方法的主要作用在于将多叉树变为二叉树，结点数据结构如下，data 为数据域，剩下两个是指针域。firstChild 指该结点第一个孩子的地址，rightSib 为该结点第一个右兄弟的地址。这样可以快速找到长子，然后通过长子的 rightSib 找到同辈。但是无法找到双亲。

完全二叉树

除最后一层外都是和满二叉树完全一致，最后一层的结点在满二叉树中的位置和目前是一致的。

• 具有 n 个节点的完全二叉树的深度为 [log2n] + 1

• 如果 i>0 , 双亲是 [i/2]

• 2i > n (n 是总结点)，那么 i 无左孩子，否则左孩子为 2i

• 2i + 1 > n ，那么 i 无友孩子，否则右孩子为 2i + 1

完全二叉树存储

由于完全二叉树的严格定义，可以用一维数组来存储一个完全二叉树，可以利用它的性质来取到一个结点双亲和儿子的下标。

链式二叉树可以节省内存，避免极端情况发生。

typedef struct BinaryNode {
    char data;
    struct BinaryNode *lchild, *rchild;
} BinaryNode, *BinaryTree;

前序遍历

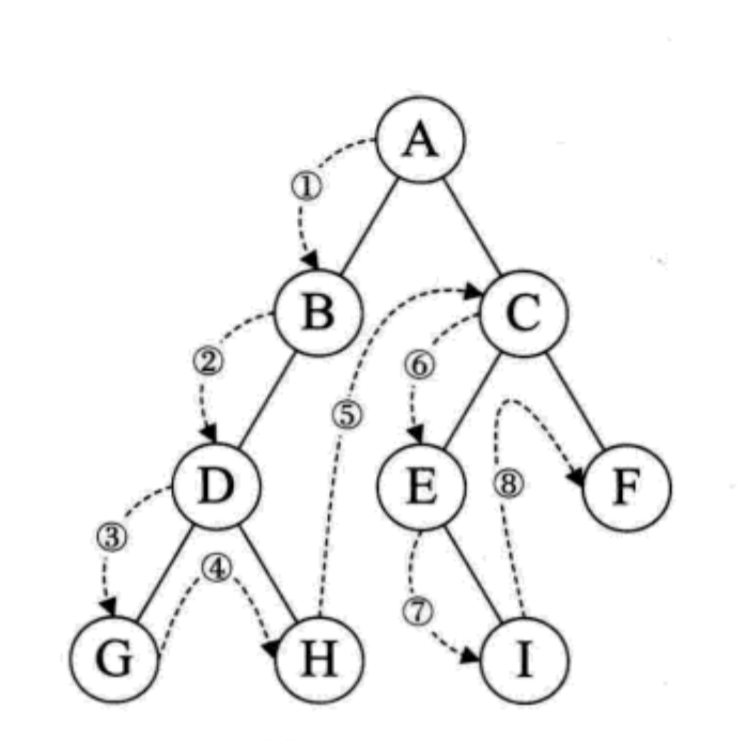
void preOrderTraverse(BinaryTree tree) {
    if (tree == NULL)
    {
        return;
    }
    printf("%c", tree->data);
    preOrderTraverse(tree->lchild);
    preOrderTraverse(tree->rchild);
}

前序，后序，中序三种遍历方式的结点游走方式都是一样的 —— 先遍历左子树然后遍历右子树。对于传入函数的指针可以理解为一个树而不是一个结点。

》》》 》》》

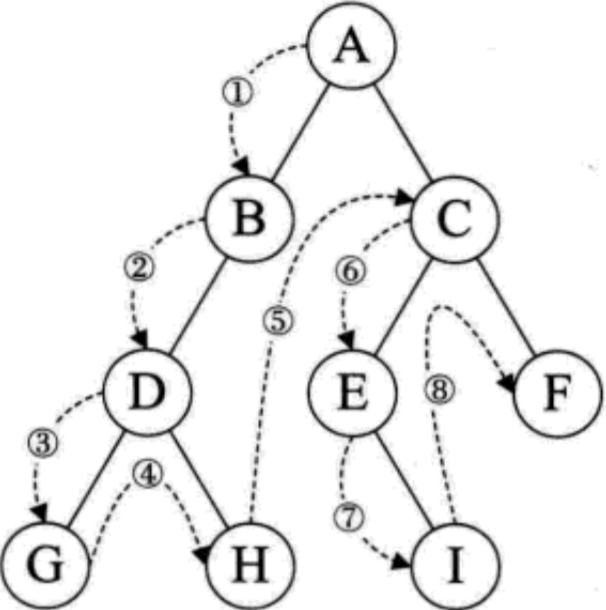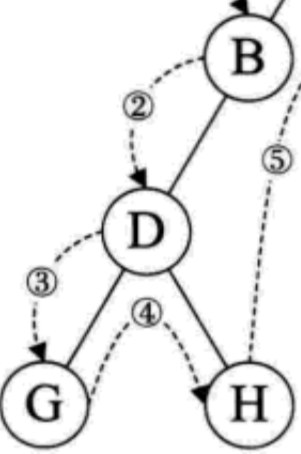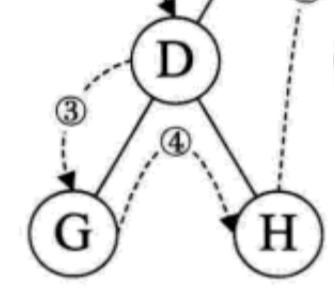
前序遍历的特点就是节点怎么游走的数据就是怎么打印的。

中序遍历

void preOrderTraverse(BinaryTree tree) {
    if (tree == NULL)
    {
        return;
    }
    preOrderTraverse(tree->lchild);
    printf("%c", tree->data);
    preOrderTraverse(tree->rchild);
}

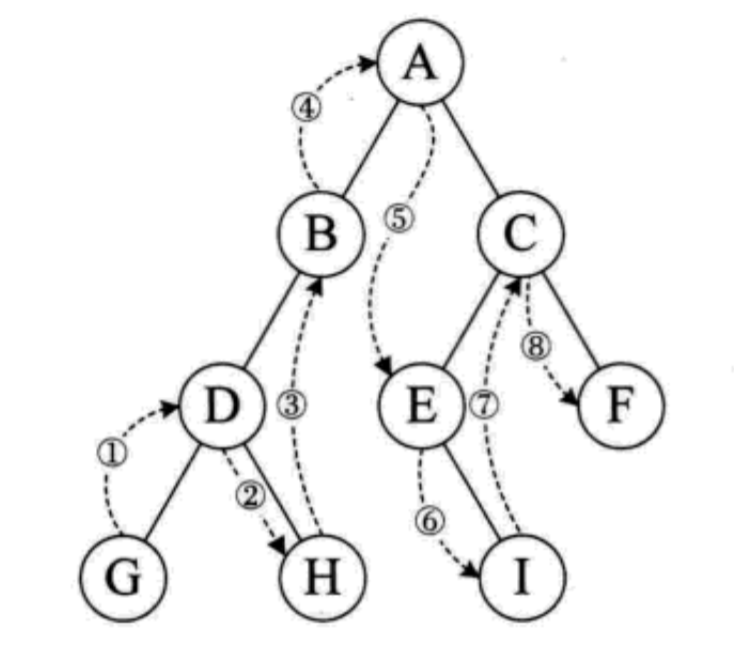
遍历完一个结点的左子树之后打印该结点，所以判断中序遍历的起点就是判断一个结点有没有左子树，如果有那么起点就在左子树中。如果没有那么就是起点。找出起点然后将每个子树看成独立的树来进行遍历。

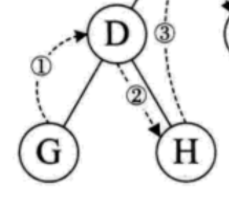
起点为 G ，将 D 看成一个子树，D 遍历完左子树，遍历右子树 H。

后序遍历

void preOrderTraverse(BinaryTree tree) {
    if (tree == NULL)
    {
        return;
    }
    preOrderTraverse(tree->lchild);
    preOrderTraverse(tree->rchild);
    printf("%c", tree->data);
}

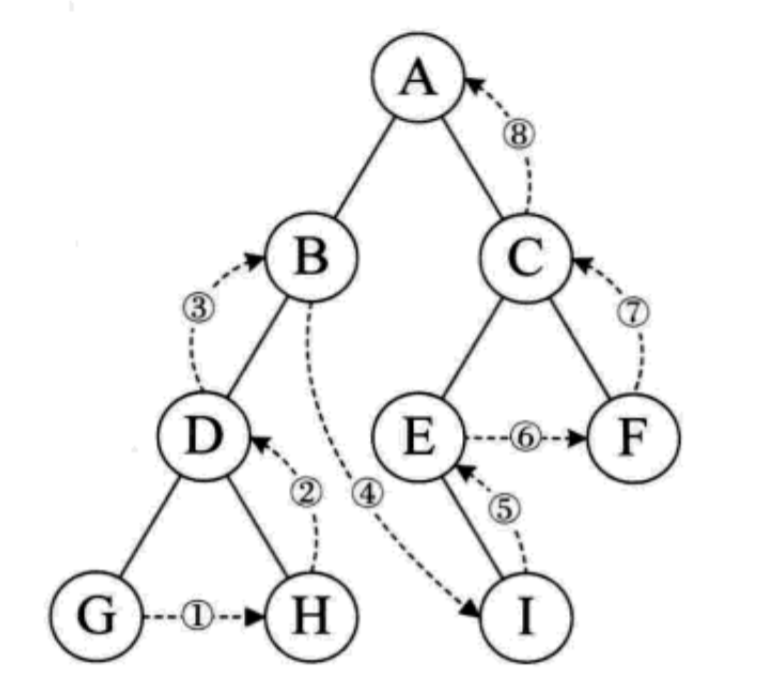
起点是左子树终点，因为首先执行的代码仍然是 preOrderTraverse(tree->lchild); D 遍历完左子树就要去遍历右子树。

树的遍历理解要领在于，从起点开始拆成最小的子树，从最小子树开始套用代码，进行理解。

二叉树的建立

已知中序遍历和其他两个任意一个遍历都可以唯一确定一棵树。

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] // preorder 和 inorder 均无重复元素

前序遍历的第一个显然是根结点，那么 3 就是根结点，接下来根据中序遍历可以确认 9 是左子树，15，20，7 是右子树。我们可以不停地找出子树的根结点来构建出树。然后我们需要做的就是为下一个递归调用准备好条件即可。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
struct TreeNode* buildTree(int* preorder, int preorderSize, int* inorder, int inorderSize){
    if (preorderSize <= 0) return NULL;
    struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->val = preorder[0];
    int index = 0; // index 是左子树的大小
    while (index < inorderSize && inorder[index] != preorder[0]) ++index;
    root->right = buildTree(preorder + 1 + index, preorderSize - (index + 1), inorder + index + 1, inorderSize - (index + 1));
    root->left = buildTree(preorder + 1, index, inorder, index);
    return root;
}

还有其他办法来构建二叉树

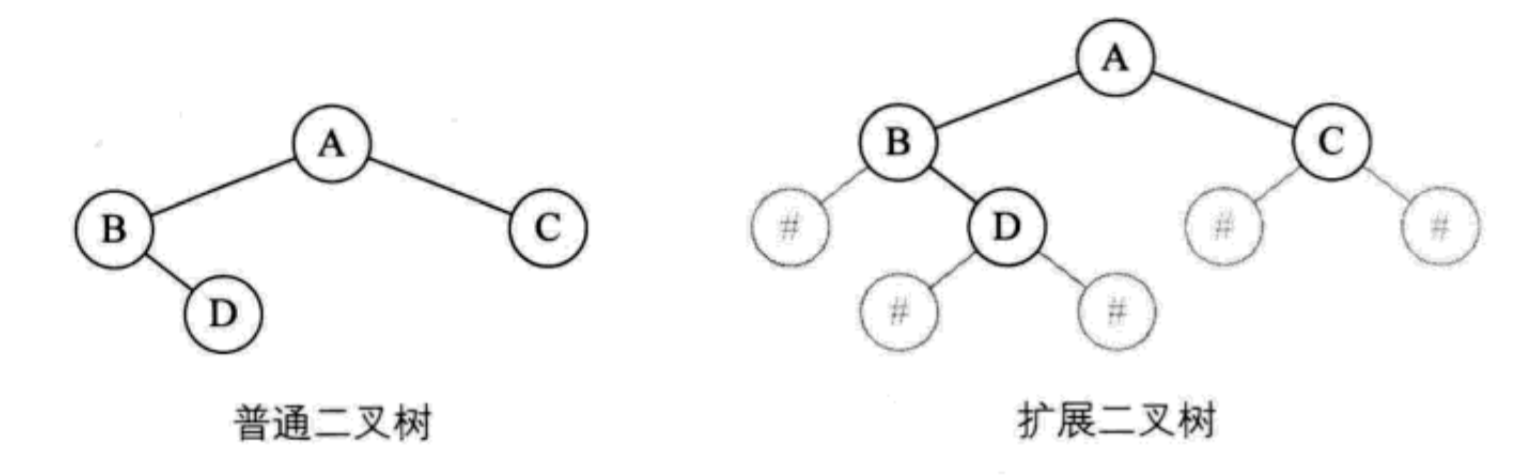
为了确认每个结点是否有左右孩子，对他进行扩展，扩展二叉树就可以做到一个遍历序列确定一颗二叉树，扩展二叉树实际上是一个完全二叉树，所以可以通过一个遍历来建立树。

typedef struct BiThrNode {
    TElemType data;//数据域
    struct BiThrNode* lchild, * rchild;
}BiThrNode, * BiThrTree;
void CreateTree(BiThrTree* tree) {
    char data;
    scanf_s("%c", &data, 1);
    if (data != '#') {
        if (!(*tree = (BiThrNode*)malloc(sizeof(BiThrNode)))) {
            printf("申请结点空间失败");
            return;
        } else {
            (*tree)->data = data;
            CreateTree(&((*tree)->lchild));
            CreateTree(&((*tree)->rchild));
        }
    } else {
        *tree = NULL;
    }
}
int main() {
    BiThrTree t;
    printf("输入前序二叉树:\n");
    CreateTree(&t);
}

递归构建树要注意的是当前函数构建的永远是当前结点，而不是它的子结点。特别体现在 19 行代码上。