整数存储

进制转换

二进制到十进制进行幂级数相加，十进制到二进制进行幂级数展开。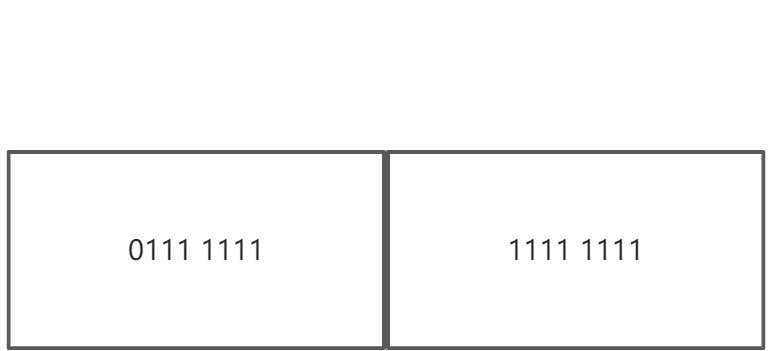

上面这个 short 型（两个字节）的变量，代表的数字就是 215 - 1 。

原码

在 10 进制中我们用 + 表示正，用 - 表示负数。一个 8 位的二进制数字 0000 0001 相当于十进制的 1。而 1000 0001 表示十进制的 -1 。按照此方法定义的二进制数据称为原码。

我们对 0000 0001 和 1000 0001 进行相加得出的结果是 1000 0010 等于十进制中的 -2 。如果整数是以原码存储的，那么加法的实现就需要额外的逻辑。

我们之所以没有在计算机中采用原码是因为我们希望能使用很简单的规则对二进制进行加减法，例如相反数进行相加时，它们的二进制会相加出优雅的 8 个 0 。

我们希望计算机硬件对于加减法的支持是能够非常简洁明了，所以我们牺牲整数的存储方式来支持计算机硬件的加减法实现。

补码

我们希望相反数进行相加时，它们的二进制会相加出优雅的 8 个 0 。要想达到 8 个 0 ，我们可以稍微绕一个弯，先达到 8 个 1，然后对 8 个 1 进行加 1就可以得到 8 个 0。

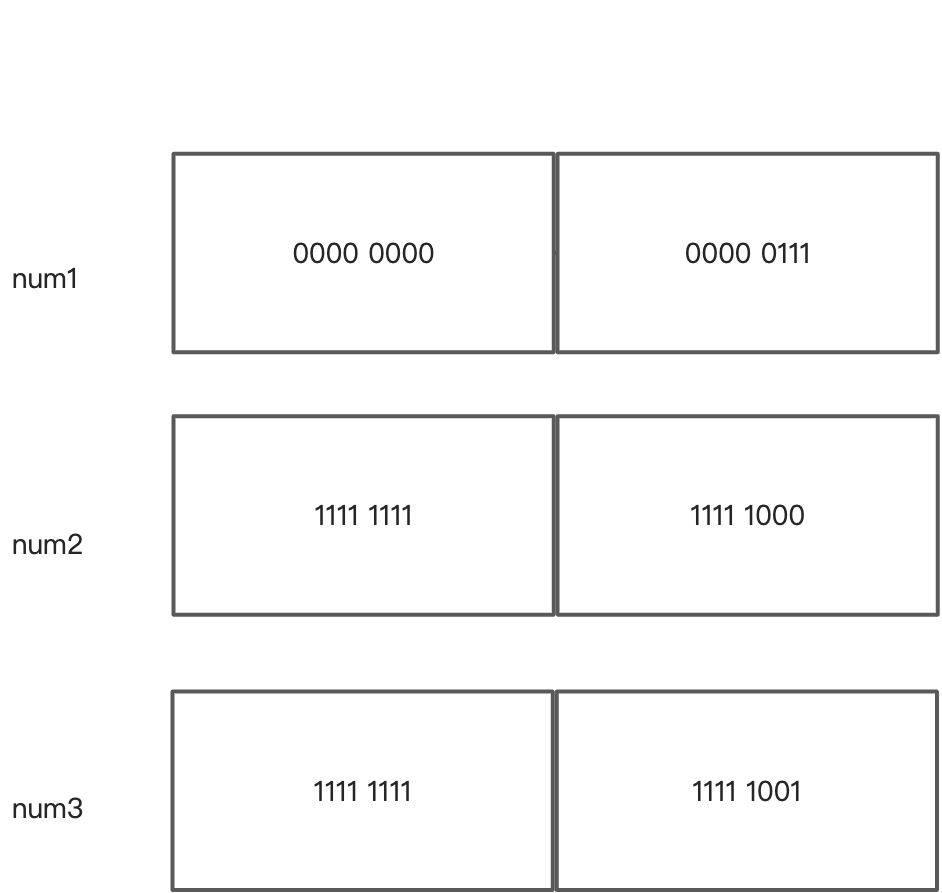
显然 num2 是 num1 的取反（反码），它们相加之后的结果再加 1 即可得到全为 0 的二进制数。我们得出结论：一个二进制的相反数是各位取反，最后+1。

我们称 num3 就是 -7（7 是num1的十进制） 的补码，补码仍然保留首位是符号位的特征，因为我们规定正数的首位一定位 0 ，算出来的负数的补码首位一定为 1。

补码的计算

正数的补码就是其本身，负数的补码是在其原码（符号位为1）的基础上，符号位不变，其余各位取反，最后+1。其实通过正数的二进制更容易算负数的补码。

反码

[+1] = [0000 0001]原= [0000 0001]反
[-1] = [1000 0001]原= [1111 1110]反

反码没有意义只是为了加起来使二进制全为 1 。整数在计算机选择补码的存储方式是为了简化计算机硬件加减法的实现。

截断

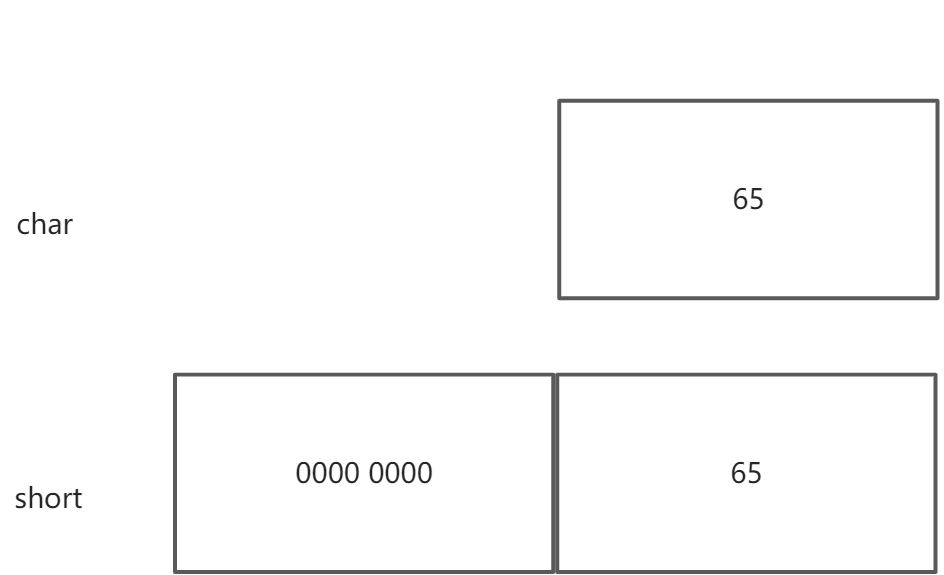
将 char 类型变量赋值给 short 类型时，计算机直接将 char 复制到 short 开始的 8 个 bit 上。short 的其他位填充为 0 。

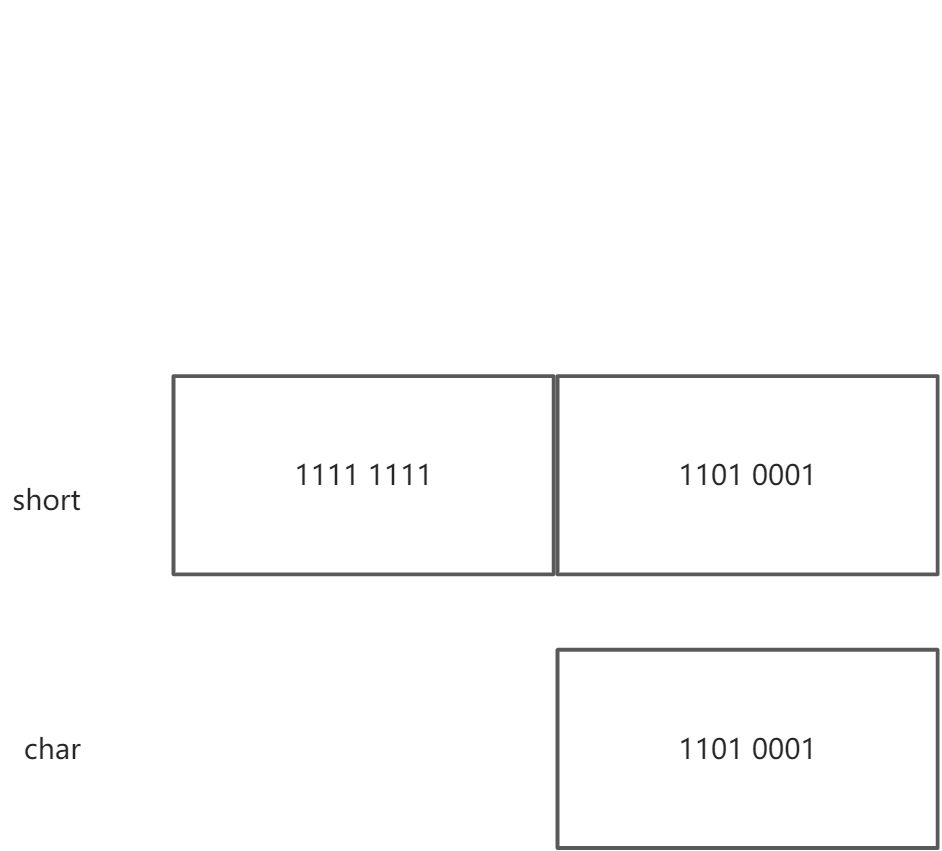
如果将 short 赋值给 char ，可能你会想计算机会使 char 中的值尽可能靠近 short 型变量，但是实际上这种截断只会进行简单地位拷贝，不会考虑数值的大小。接下来考虑负数的赋值。

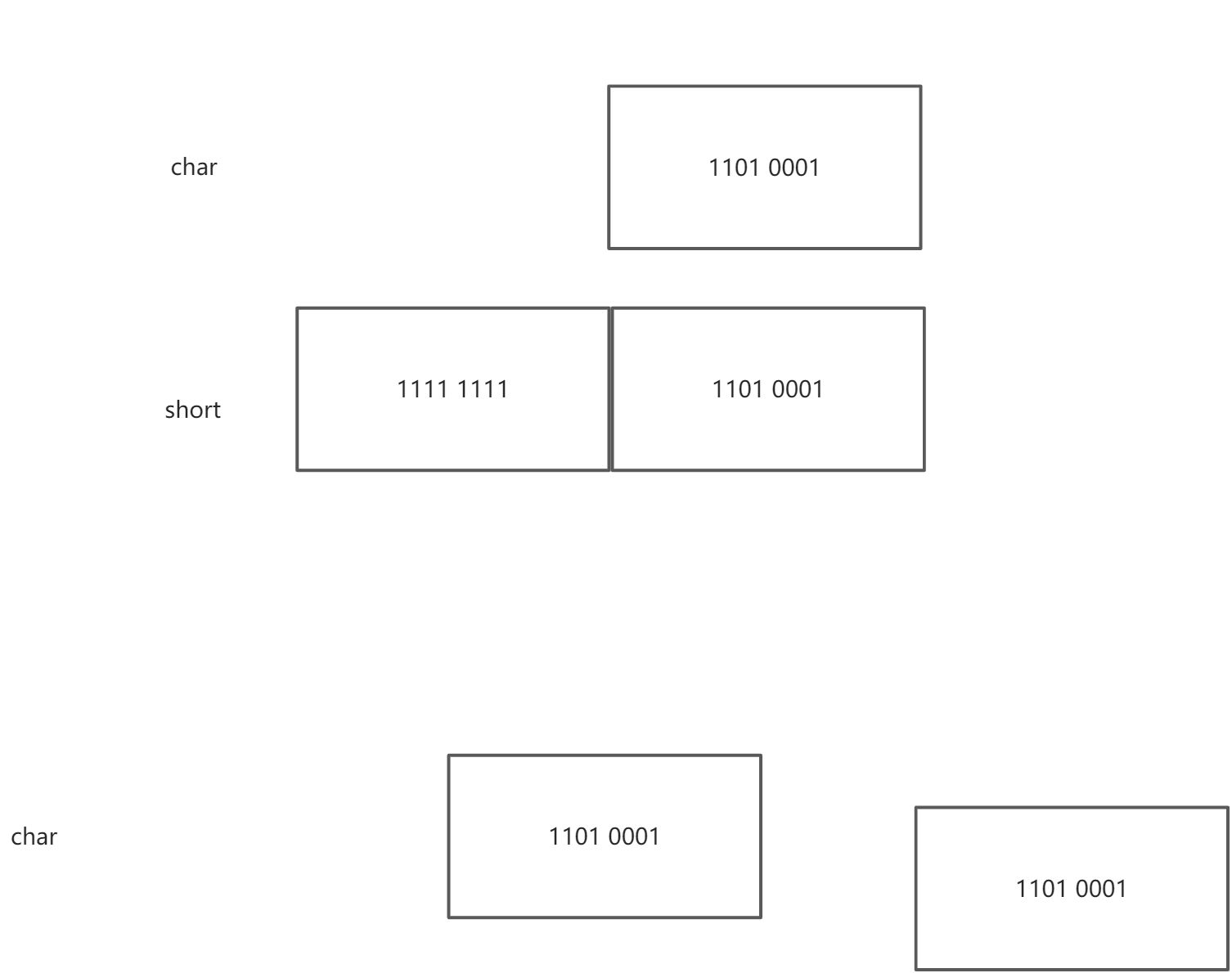
将上面 char 的值赋值给 short，计算机会将首位的符号位填充其他位，这叫做符号扩展。