我国比例尺地图采用高斯-克吕格投影，通常按6度和3度分带投影。
    具体分带法是：6度分度从本初子午线开始，按经度差6度为一个投影带自西向东划分。

    具体方法是，规定中央经线为X轴，赤道为Y轴，中央经线与赤道交点为坐标原点，x值在北半球为正，南半球为负，y值在中央经线以东为正，中央经线以西为负。由于我国疆域均在北半球，x值均为正值，为了避免y值出现负值，规定各投影带的坐标纵轴均西移500km，中央经线上原横坐标值由0变为500km，也就是我们经常遇见的东伪偏移量false easting。为了方便带间点位的区分，可以在每个点位横坐标y值的百千米位数前加上所在带号，如20带内A点的坐标可以表示为YA=20 745 921.8m。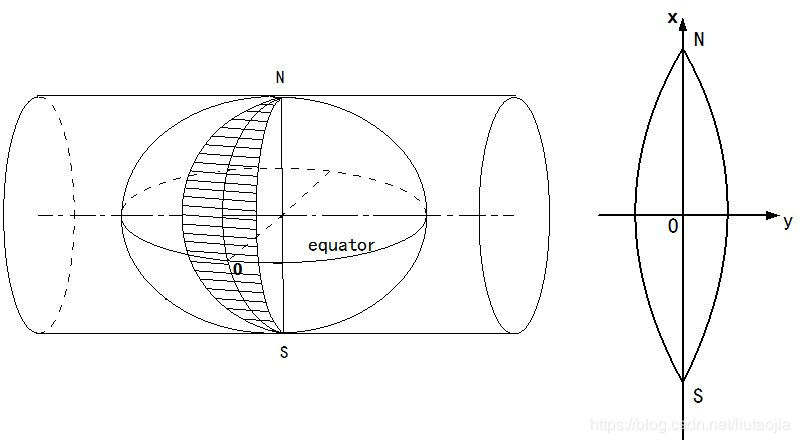
    坐标系笔记： - 图1
    高斯-克吕格投影正算公式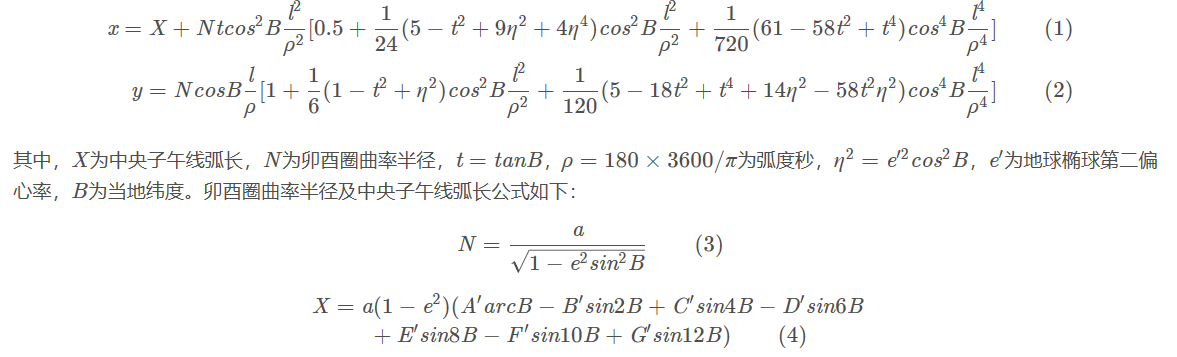
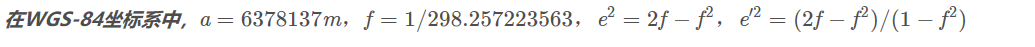
    image.png
    image.png
    image.png
    Matlab程序：
    function [x,y] = GaussProWGS84(Lat,Lon)
    % Lat: Latitude(rad)
    % Lon: longitude(rad)
    Lat = Latpi/180;
    Lon = Lon    pi/180;
    MedLon = 114pi/180; %武汉的中央子午线经度
    Eth.R0 = 6378137.0;
    Eth.f = 1/298.257223563;
    Eth.e12 = 2    Eth.f - Eth.fEth.f; % 0.00669437999014132
    Eth.e22 = Eth.e12/((1 - Eth.f)    (1 - Eth.f));
    %% 高斯投影正算公式
    RN = Eth.R0/sqrt(1 - Eth.e12sin(Lat)sin(Lat));
    Lon = Lon - MedLon;
    Lon2 = LonLon;
    Lon4 = Lon2    Lon2;
    tnLat = tan(Lat);
    tn2Lat = tnLattnLat;
    tn4Lat = tn2Lat    tn2Lat;
    csLat = cos(Lat);
    cs2Lat = csLatcsLat;
    cs4Lat = cs2Lat    cs2Lat;
    Eta2 = Eth.e22cs2Lat;
    NTBLP = RN    tnLatcs2LatLon2;
    coe1 = (5 - tn2Lat + 9Eta2 + 4Eta2Eta2)cs2LatLon2/24;
    coe2 = (61 - 58    tn2Lat + tn4Lat)cs4LatLon4/720;
    x = Merdian(Eth,Lat) + NTBLP(0.5 + coe1 + coe2);
    NBLP = RN    csLatLon;
    coe3 = (1 - tn2Lat + Eta2)    cs2LatLon2/6;
    coe4 = (5 - 18    tn2Lat + tn4Lat + 14Eta2 - 58tn2LatEta2)cs4LatLon4/120;
    y = NBLP    (1 + coe3 + coe4) + 500000;
    end
    function X0 = Merdian(Eth,Lat)
    % REF//过家春.子午线弧长公式的简化及其泰勒级数解释[J].测绘学报,2014,43(2):125-130.
    S0 = Eth.R0(1 - Eth.e12);
    e2 = Eth.e12;
    e4 = e2    e2;
    e6 = e4e2;
    e8 = e6    e2;
    e10 = e8e2;
    e12 = e10    e2;
    A1 = 1 + 3e2/4 + 45e4/64 + 175e6/256 + 11025e8/16384 + 43659e10/65536 + 693693e12/1048576;
    B1 = 3e2/8 + 15e4/32 + 525e6/1024 + 2205e8/4096 + 72765e10/131072 + 297297e12/524288;
    C1 = 15e4/256 + 105e6/1024 + 2205e8/16384 + 10395e10/65536 + 1486485e12/8388608;
    D1 = 35    e6/3072 + 105e8/4096 + 10395e10/262144 + 55055e12/1048576;
    E1 = 315    e8/131072 + 3465e10/524288 + 99099e12/8388608;
    F1 = 693e10/1310720 + 9009e12/5242880;
    G1 = 1001e12/8388608;
    X0 = S0    (A1Lat - B1sin(2Lat) + C1sin(4Lat) - D1sin(6Lat) +…
    E1    sin(8Lat) - F1sin(10Lat) + G1sin(12Lat));
    end

    墨卡托投影，又称正轴等角圆柱投影，由荷兰地图学家墨卡托(G.Mercator)于1569年创拟。假设地球被套在一个圆柱中，赤道与圆柱相切，然后在地球中心放一盏灯，把球面上的图形投影到圆柱体上，再把圆柱体展开，就形成以一幅墨卡托投影的世界地图（如下图）。因其等角特性，广泛应用与航空、航海中。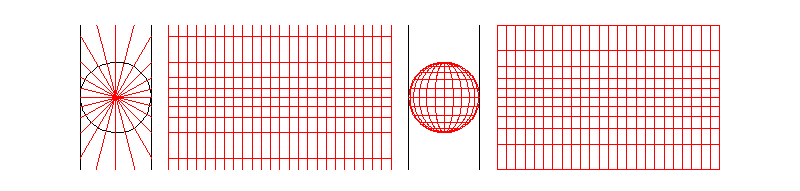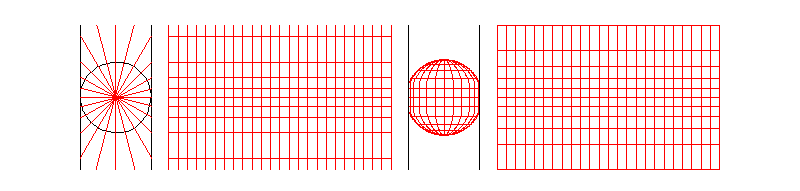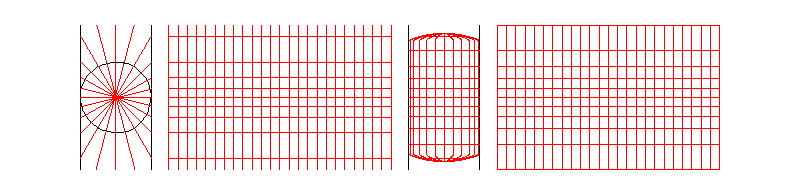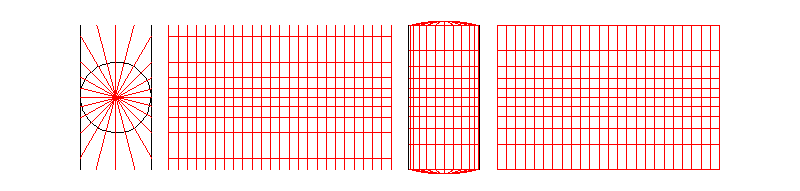
    20131028160043109.gif
    x轴刻度是等距的，y轴方向越靠近两级变形越大。假设墨卡托投影的坐标系原点为（0,坐标系笔记： - 图6），表示x轴为赤道，y轴则在经度为坐标系笔记： - 图7处垂直于赤道。
    墨卡托投影公式：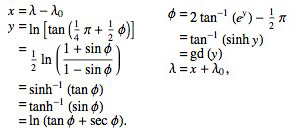
    20131028163124250.jpg
    左侧为正算，右侧为逆运算。
    (坐标系笔记： - 图9,坐标系笔记： - 图10)为经纬度，对应的墨卡托平面坐标为（x    R，y*R）。y方向的距离只有在赤道附近才是接近实际距离的。