B-树就是B树，平衡多路查找树，不只是只有两个节点，而且也是平衡的，<br />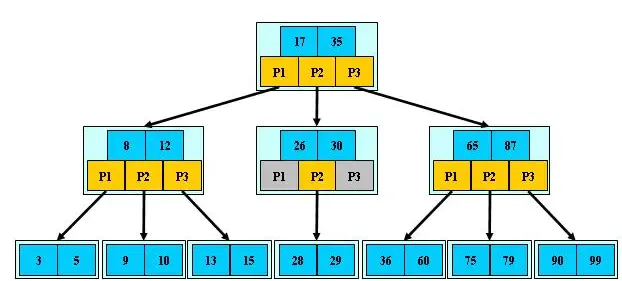![](https://cdn.nlark.com/yuque/0/2021/webp/22438777/1636446591092-2d816423-ca54-4ad0-8b27-cf9aff26f0d0.webp?x-oss-process=image%2Fresize%2Cw_622%2Climit_0#from=url&height=248&id=G8hi7&margin=%5Bobject%20Object%5D&originHeight=281&originWidth=622&originalType=binary&ratio=1&status=done&style=none&width=549)

特性：

B树种所有孩子节点数种的最大值称为B树的阶，记作M
树中的每个节点至多有M棵子树（如果定义了M，B树种任何节点的子节点数量都不能超过M）
若根节点不是叶子节点，则至少有两棵子树
除了根节点之外的所有非叶子节点至少有P个子节点（m/2）<=p <=m ，向上取整
所有的非叶子节点中包含 n，K，A
K(k1,k2,k3….kn),关键码，是真实数据，存放在线性表中，且从左至右升序排列
A(a1,a2….An),指针，指针数比关键码数量多1，每个数据码都有两个指针
n为关键码个数（m/2）-1 <=n <=m-1
所有的叶子节点都在同一层次上，即所有的叶子节点具有相同的深度，并且不带信息，（可以当作是外部节点，或者查找失败的节点，实际上这些节点不存在，指向这些节点的指针为空）

数据查找

跟二叉树类似，都是从根节点开始比较，判断当前节点是否存在，不存在比较大小（查询数据是磁盘IO，比较是内存）进去到子节点中，二叉树只有左右，B树则是多个，循环操作，直到返回数据，或者查询失败，x
虽然B树的高度比二叉树，低，但是节点的数据量大，也不行，数据比较是在内存完成的，如果节点过多（m）会导致比较次数太多而影响性能，

数据插入（跟2-3树类似）

一般是插入到叶子节点，通过检索可以确定关键码（数据）应插入的节点位置，分为2种情况
1.要插入的节点，关键码数量小于m-1，直接插入
2.要插入的节点，关键码数量等于-1.
则将引起节点的分裂,以中间关键码为界将节点一分为二，产生一个新节点，将新节点（中间节点）关键码插入到父节点（k-1层）种
重复上述操作，直到不会分裂，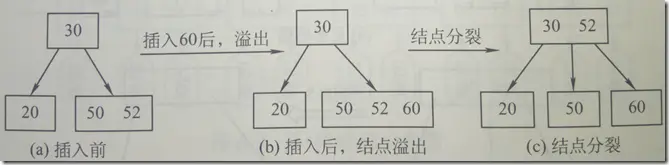

数据删除

关键码删除，也是分为，叶子节点跟非叶子节点，非叶子节点可以通过查找后继元素，替换，就变成了删除叶子节点，

如果查询不到，就不存在key，删除失败
删除叶子分为四种情况
1.删除节点的关键码（key）个数，大于（m/2）-1，
直接删除，（删除26）
2.删除节点的关键码（key）个数，小于（m/2）-1，且兄弟节点的key个数大于（m/2）-1，
删除key28之后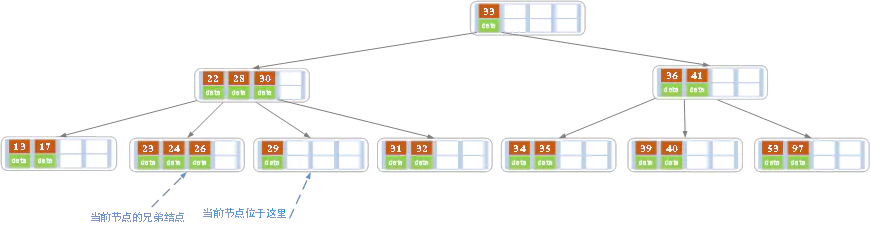

将父节点的key（28），下移至删除节点，兄弟节点的一个key（26），上移到父节点中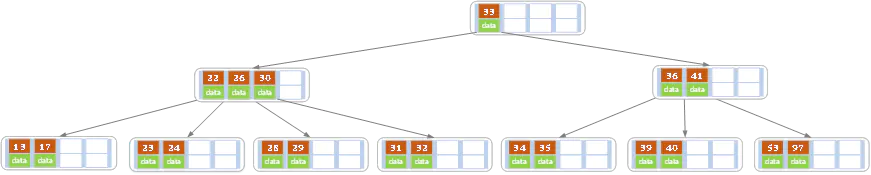

3.删除节点的关键码（key）个数，小于（m/2）-1，且兄弟节点的key个数小于等于（m/2）-1，
将父级节点中的key，下移，与当前节点跟兄弟节点合并，形成一个新的节点，原父节点中的key的两个孩子指针，变为一个，指向新节点
上图删除key32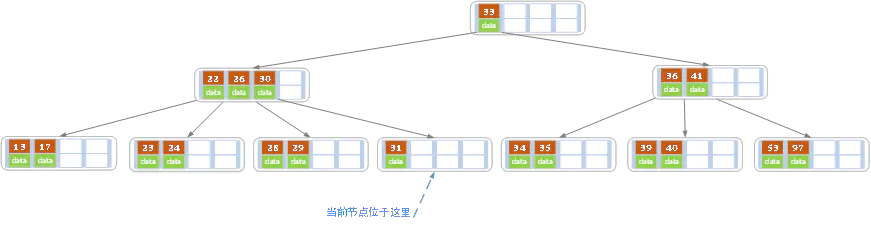

将父节点的key(30)下移，与两个节点，合并称为新节点，并指向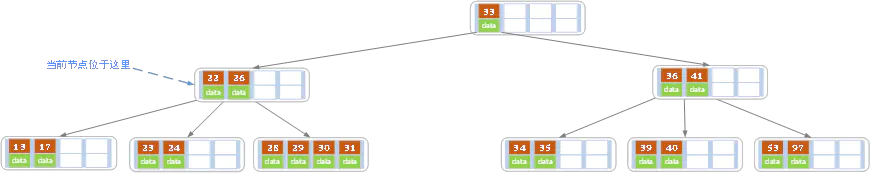

4.因为动了父节点中的key，需要对父节点进行考虑，
情况3的时候没有事，但是如果改为删除40，就会产生这个结果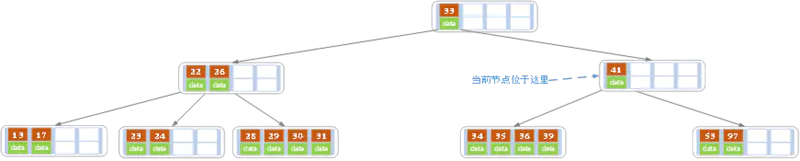

此刻父节点就不符合条件了，考虑情况2跟3，父节点的key数量也不够，指向情况三，下拉，合并