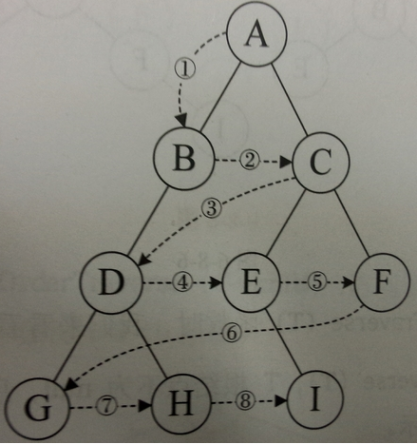
树是一种很特别的数据结构,树这种数据结构叫做树就是因为它长得像一棵树,但是这颗树确实一棵倒着的树,根在上,叶在下,<br />树是图的一种,区别是,树是没有环的,而图是可以有环,(环:从节点按照顺序出发,经过多个节点,能否回到本节点)<br />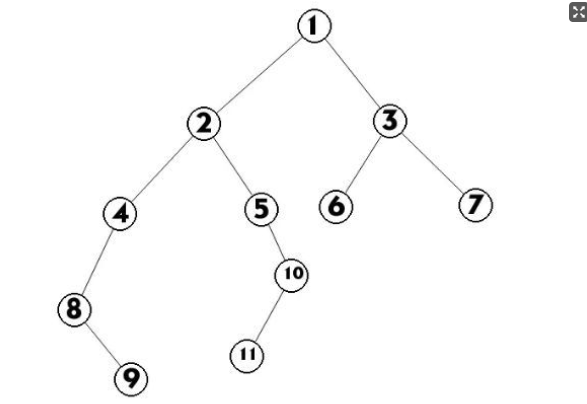
树(Tree)基本概念:
树是由节点或顶点和边组成的(可能是非线性的)且不存在着任何环的一种数据结构,
没有节点的树成为空(null或empty)树,
一棵非空的树包含一个根节点,还(很可能)由很多附加节点,所有的节点构成一个多级分层结构
树的一些术语定义:
节点的度:一个节点含有的子树的个数称为该节点的度
叶节点:度为9 的节点成为叶节点
分支节点:度不为0 的节点
父节点:若一个节点含有子节点,则这个节点称为起子节点的父节点
子节点:一个节点含有的子树的根节点,称为该节点的子节点
兄弟节点:具有相同父节点的节点,互称为兄弟节点,
树的度:一棵树中最大的节点的度称为树的度
节点的层次:从根开始定义起,根为第一层,根的子节点为第二层,以此类推
树的高度或者深度:树中节点的最大层次
堂兄弟节点:双亲在同一层的节点互为堂兄弟
节点的祖先:从根到该节点所经分支上的所有节点
子孙:以某节点为根的子树种任一节点都称为该节点的子孙
森林:由m(m>=0)棵不相交的树的集合称为森林
树的表现方法
三种表现方法,分别是图像表现法,符号表现法和遍历表示法
图像表示法
就是上图所示,最常见,最普通的
符号表现法:
没有其他两种常见,但是比较使用,
同层子树与它的根节点用圆括号括起来,同层子树之间用逗号隔开,最后用闭括号括起来,
表现为:(1(2(6,7(14),8(15(19))),3(9(16)),4(10,11(17(20)),12),5(13(18(21)))))
遍历表现法:
分为前序遍历,中序遍历,后序遍历,层序遍历(不常用)
前序,中序,后序,指的的是根(中)节点的访问顺序,前序遍历是中左右,中序遍历是左中右,后序遍历是左右中
前序遍历:
先访问根,再先序编辑左子树,最后编辑右子树,
从根开始,一直访问左子树,左子树到达叶子节点后,访问右子树,没有的话,向父级寻找,找到右子树后,
继续上边的 操作,将右子树,当成根,寻找左子树,一直这样操作,到最后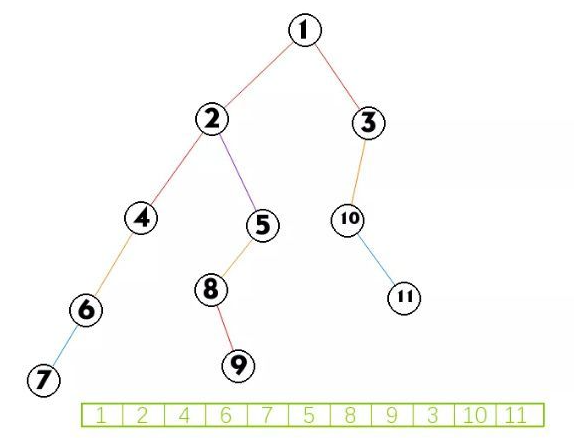
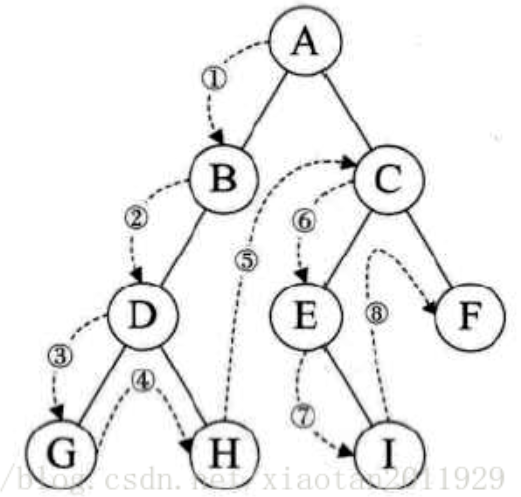
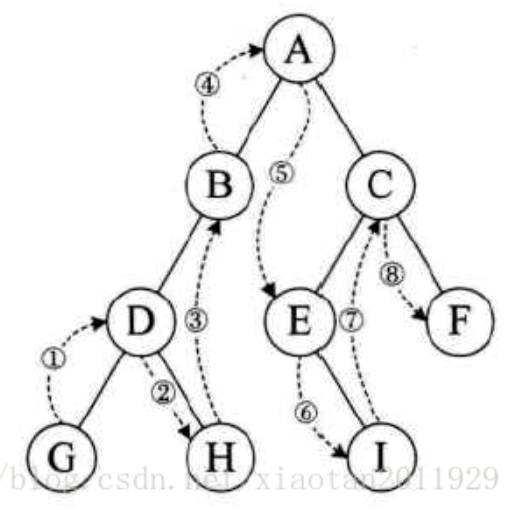
中序遍历:
先中序左子树,访问根,最后中序遍历右子树
查询左子树,直到左子树到达叶子节点,输出节点,然后输出父节点,查找父节点的右子树,输出,然后向上寻找,
父节点的父节点,然后寻找父节点的父节点的右子树,一直上面的循环,到最后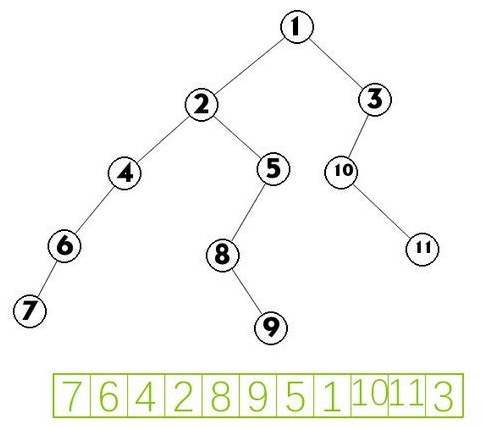
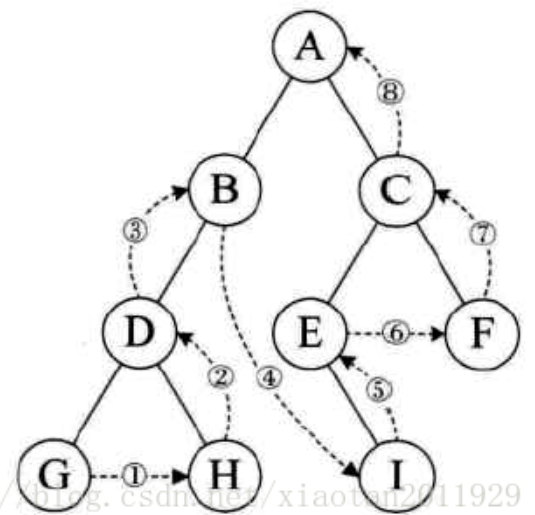
后序遍历:
先后序左子树,在后序右子树,最后访问根
查询左子树,直到左子树到达叶子节点,输出节点,然后查找父节点的右子树,输出,然后输出父节点,然后向上寻找,
父节点的父节点,然后寻找父节点的父节点的右子树,一直上面的循环,到最后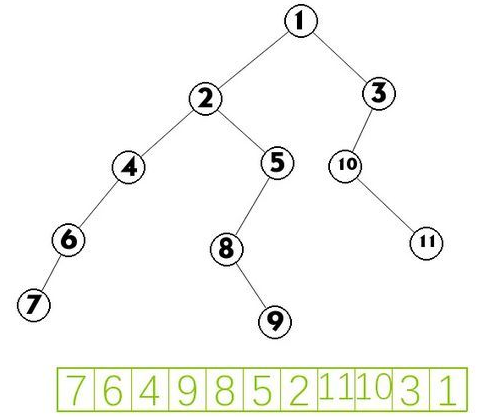
层序遍历:
使用不是很多 从根节点开始,输出,然后第二层,自左向右输出,然后第三层,继续,知道结束