2-3树满足二叉搜索树的基本特性，唯一特别的是2-3树的一个节点可以存一个元素也可以存两个，子节点可以是2个或者三个，所以叫2-3树
此外除了2-3树和2-3-4树，一样的逻辑特性
节点有两个元素，子节点的范围是：小于第一个，第一个第二个之间，大于第二个
2-3树 - 图1

特性：

一定不是绝对平衡的树，也就是深度一样，平衡因子为0

添加节点

添加元素就是将元素放在符合的节点中，先放进去，如果元素超出，就分裂出子集，再加一层，如果不平衡了，就将节点向上融合，父节点如果也超出范围了，就再向上分裂，重复这个操作，直到平衡
1.插入42，37 因为可以存放两个节点，所以是这样的
37 42
2.添加12 ，会先加入节点中，根据平衡树类似的原理再分裂
12 37 42 image.png
3.添加18 ，根据平衡树原理，小于37 进入到左子树， 左子树12 只有一个元素，还可以再添加一个
image.png
4.添加一个6 根据平衡树原理，小于37 进入到左子树， 左子树已经有两个元素了，先添加进去，根据平衡树原理再分裂到子集
image.pngimage.png
但是发现此刻树不是绝对平衡，需要将12 于37 融合
image.png
5.添加11 到了左子树中
image.png
6.添加元素5 先添加到左子树中，超出元素数量，分裂到子集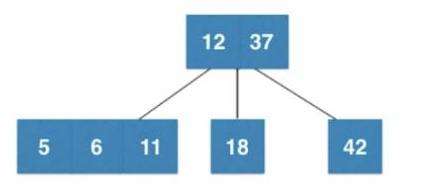
image.pngimage.png
分裂到子集之后，发现不平衡，将6向上融合，发现根节点元素超了，再分裂向上融合，提取出一个来，当根节点
image.pngimage.png

删除元素

由于2-3树时绝对平衡树，所以，删除的只有叶子节点，跟非叶子节点之分
删除叶子节点
1.如果删除的元素所在的节点内不止一个元素的话，直接删除就好，不影响平衡
2.删除的元素所在节点，只有一个元素，删除后，影响平衡 比如 删除 14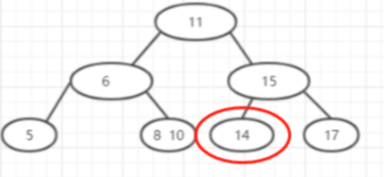
image.png
为了保持节点的深度，将父节点 15 向下移动，或者找多元素兄弟节点弥补一下（比如删除4）
image.png或者
image.png
如果是将父节点下移，如果此时父节点空了，空位置需要父节点的父节点补充，随后发现子集位置不对，需要合并一下
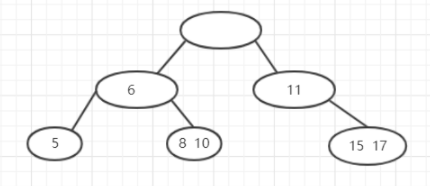
image.pngimage.png
最后将父级合并在一起，
image.png
删除非叶子节点
删除12，12是根节点，所以选择左子树最右边（后继节点） 代替他，11移走以后，就需要从父节点中把10移下来保持叶子结点的深度，同时把8和10合并。
2-3树 - 图18

转换红黑树

其实红黑树就是用二叉树来表示2-3树的
因为2-3树不止一个子树，元素个数可以有两个，
其实双元素的2-3树可以换一种展示方式 ，将两个子集都连接到b下边
image.png
再调整一下b c 的关系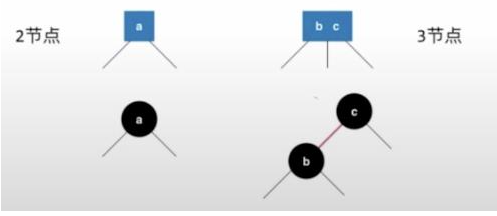
image.png
就变成了2叉树，但b跟c 是同等地位，现在变成子集了，为了显示bc是一起的，同一级别的，用不同颜色表示
image.png
这就是红黑树的由来了，红黑就是一个状态标记，本质上是2-3树，红色节点是2-3树左侧的分下来的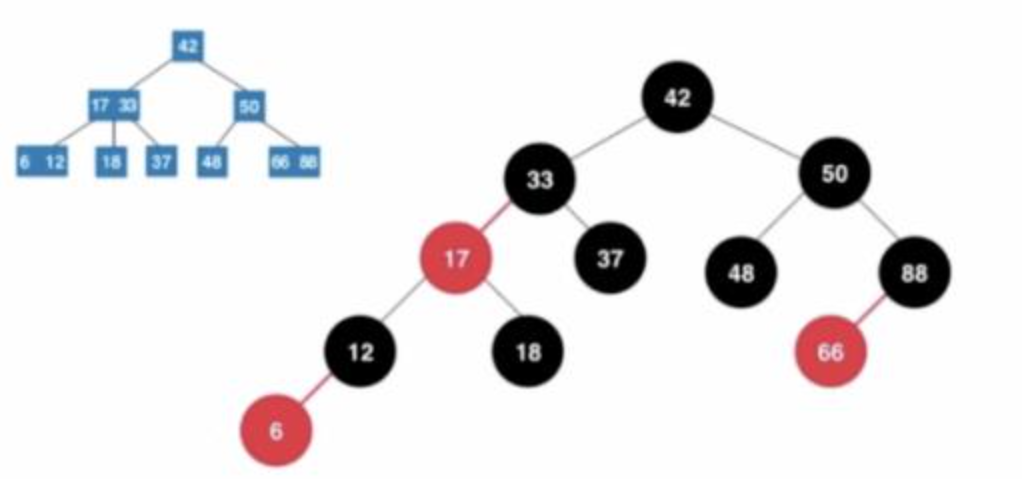
image.png
红黑树的一些特性就可以解释通了
1.红黑树的节点是红色或者黑色—->红色就是2-3树中，两个元素的节点，靠左的那个节点，拉下来，就是红色
2.根节点是黑色的 ——>因为两个元素的时候，左侧的元素拉下来，留下的那个就是黑节点，也就是根节点
3.每个叶子节点是黑色的 ——>这里叶子节点，是指为空(NIL或NULL)的叶子节点 ,因为每个叶子结点只有一个元素嘛，不可能为红色的
4.节点是红色的，子节点必须是黑色的———>因为红色节点是双元素节点左侧元素下拉形成的，那么下面的两个节点不管是否也会下拉，留在上面的一定是右测的元素，也就是黑节点，不会出现红红，
5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点 ——->因为红黑树是2-3树等价过来的，而2-3树是绝对平衡的，红色节点是原本的双元素下拉造成的，也就是说去掉红色节点之后，展示的就是2-3树，绝对平衡，