AVl树是带有平衡条件的二叉查找树，和红黑树相比，它是严格的平衡二叉树，
平衡条件必须满足（所有节点的左右子树高度差不超过1），
不管我们是执行插入还是删除操作，只要不满足上面的条件，就要通过旋转来保持平衡，而旋转式非常耗时的

使用场景

AVl树适合用于插入删除次数比较少，单查找多的情况
也在windows进程地址空间管理中得到了使用
旋转的目的式为了降低树的高度，使其平衡

特点

AVL树是一棵二叉搜索树
AVL树的左右子节点也是AVL树
AVL树拥有二叉搜索树的所有基本特点
没个节点的左右子节点的高度之差的绝对值最多为1，即平衡因子范围为（-1，1）
平衡因子：
某节点的左子树于右子树的高度差，即为该节点的平衡因子，平衡二叉树的平衡因子不会大于一，只能取0或者1
最小失衡子树：
在新插入的节点向上寻找，以第一个平衡因子的绝对值超过1的节点为根的子树，称为最小不平衡子树，
也就是说，一棵失衡的树，是由可能有很多棵子树同时失衡的，而这个时候我们只要调整最小的不平衡子树，就能够将不平衡的树，调整为平衡的树

旋转

平衡二叉树的失衡调整主要是通过旋转最小失衡子树来实现的，根据旋转的方向有两种处理方式，左旋跟右旋
旋转的目的是减少高度，通过降低整棵树的高度来平衡，哪边的树搞，就把那边的树向上旋转

左旋：

当失衡节点的右子树高于左子树的时候，需要对节点进行左旋操作（将左子树下沉）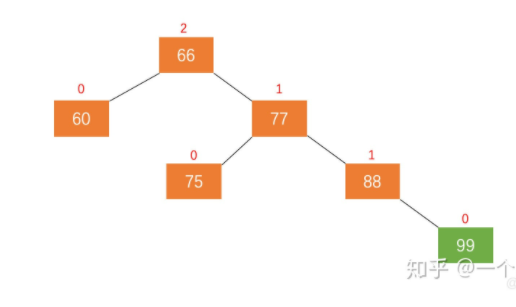

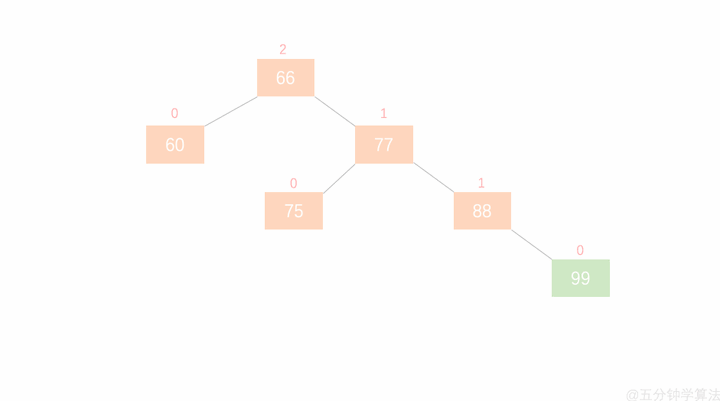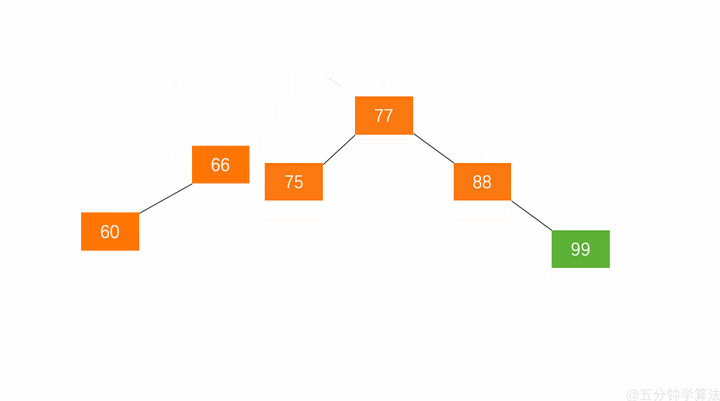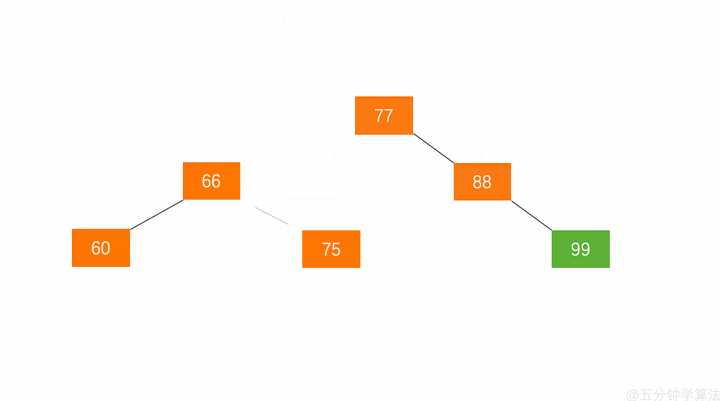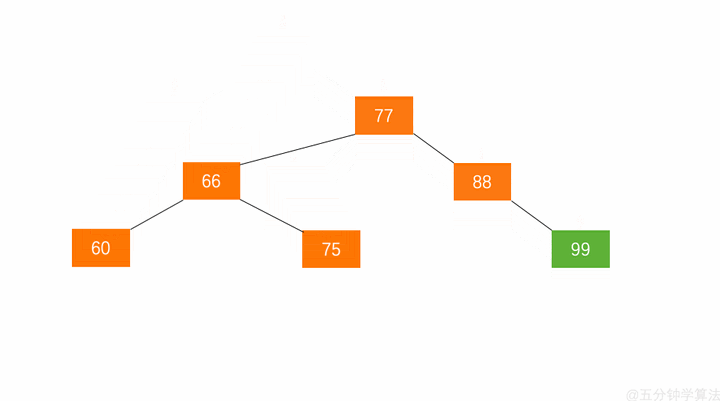
1.节点的右孩子替代此节点的位置
2.右孩子的左子树变成该节点的右子树，
3.节点本身变为右孩子的左子树

右旋：

当失衡节点的左子树高于右子树的时候，需要对节点进行右旋操作（将右子树下沉）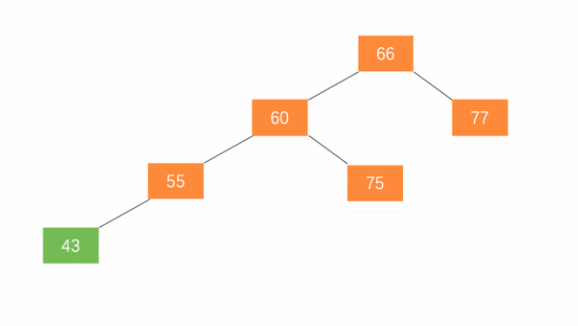

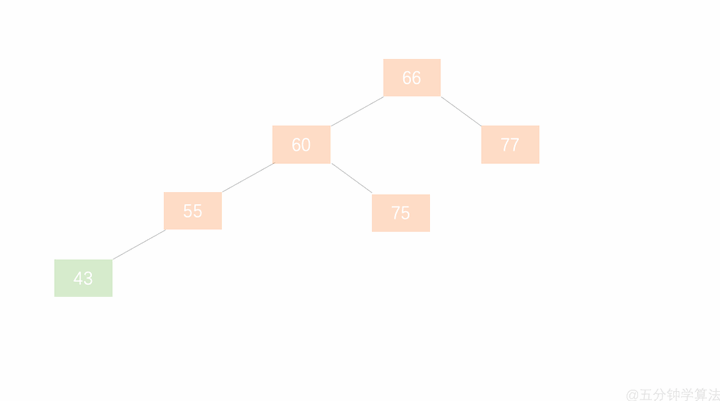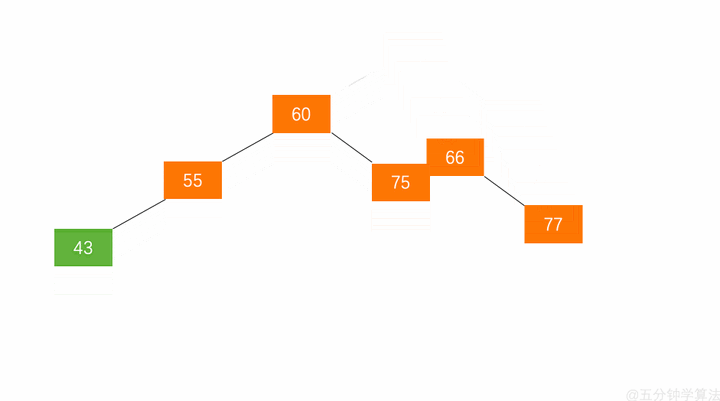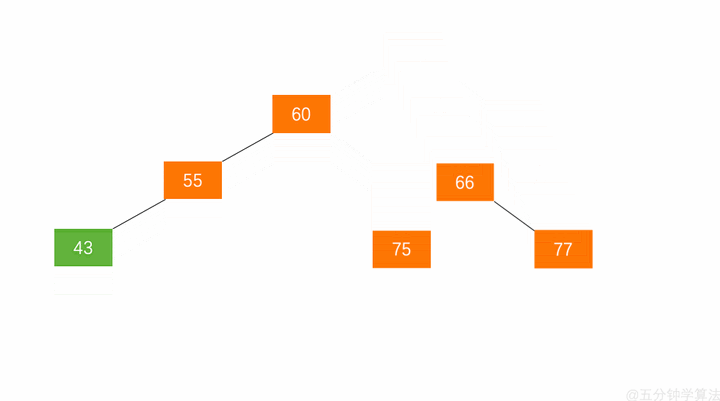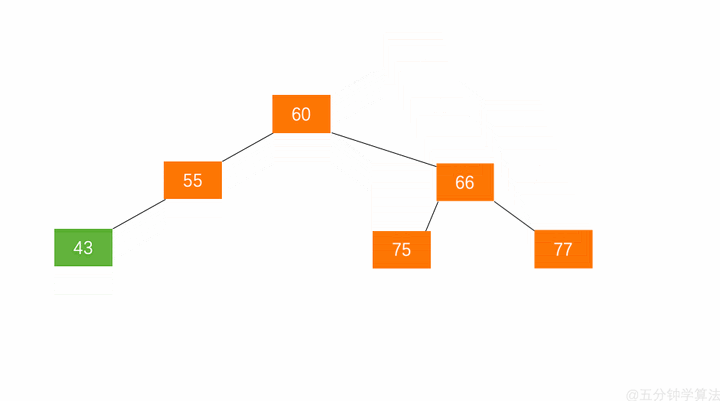
1.节点的左孩子替代此节点的位置
2.左孩子的右子树变成该节点的左子树，
3.节点本身变为左孩子的右子树

添加方式

添加就是将添加节点先添加树的底部，叶子节点，判断平衡，不平衡的通过旋转操作使得AVL树保持平衡，分四种情况
A的左孩子的左子树插入节点(LL)
平衡方法：右旋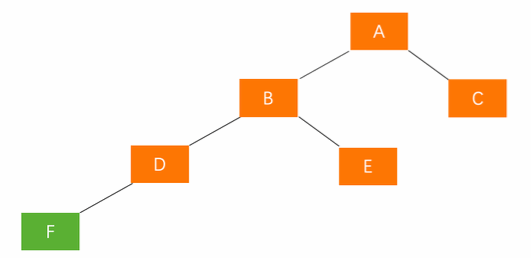

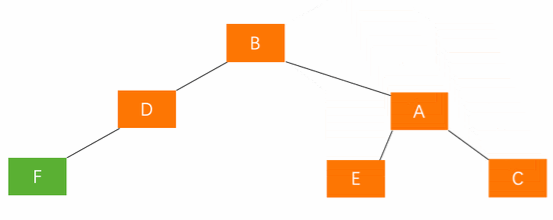
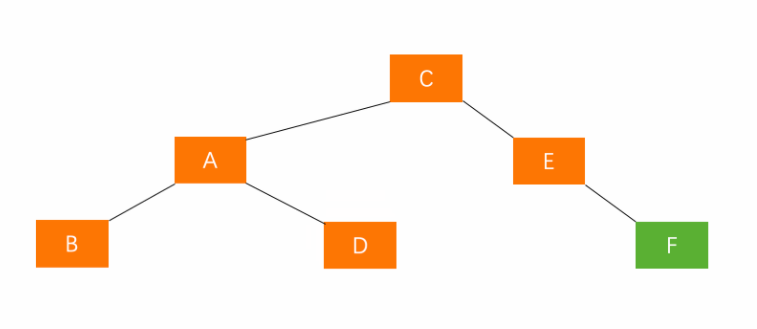
A的右孩子的右子树插入节点(RR)
平衡方法：左旋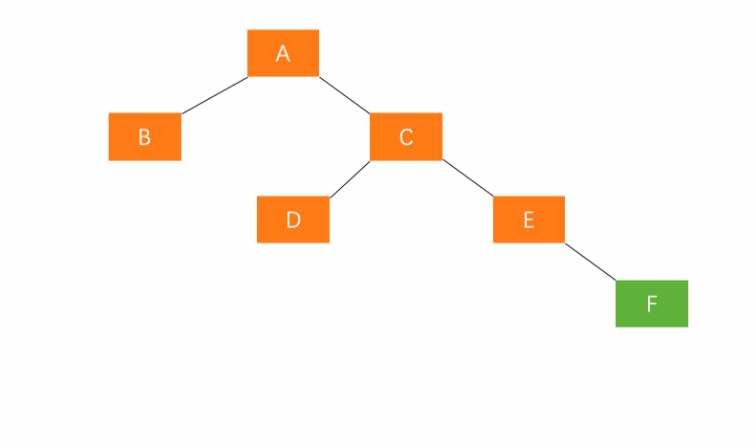

A的左孩子的右子树插入节点(LR)
平衡方法：
对失衡节点的左子树进行左旋
对失衡节点进行右旋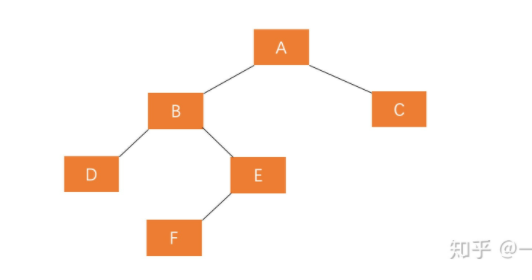


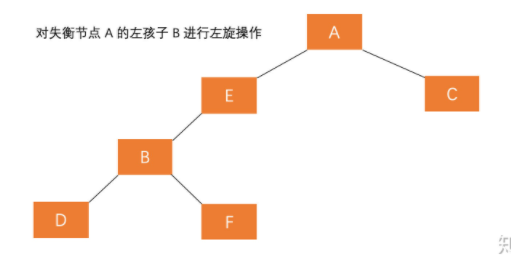
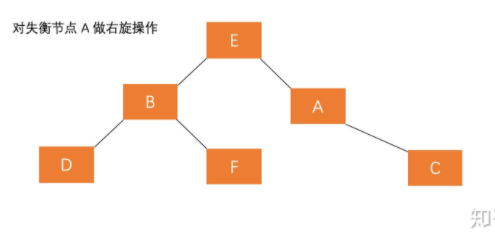
A的右孩子的左子树插入节点(RL)
平衡方法：
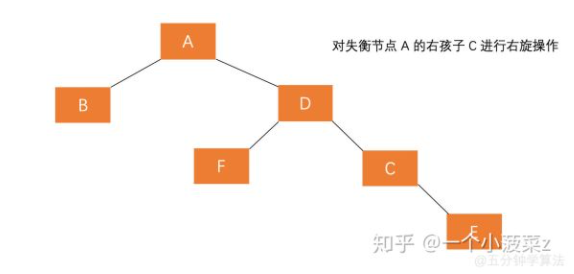
对失衡节点的右子树进行右旋
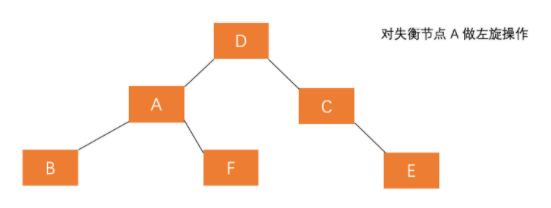
对失衡节点进行左旋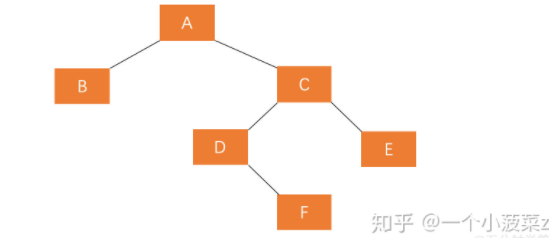


总结
| 插入方式 | 描述 | 旋转方式 |
| LL| 在 A 的左子树，根节点的左子树上插入节点而破坏平衡 | 右旋转 |
| RR | 在 A 的右子树，根节点的右子树上插入节点而破坏平衡 | 左旋转 |
| LR | 在A的左子树，根节点的右子树上插入节点而破坏平衡 | 先左旋后右旋 | （左子树左旋，根节点右旋）
| RL | 在 A 的右子树，根节点的左子树上插入节点而破坏平衡 | 先右旋后左旋 |（右子树右旋，根节点左旋）

删除方式

删除情况比较麻烦，先分为删除叶子节点，跟非叶子节点，每种各自分了几种情况，不过，删除非叶子节点最终都会通过置换，变成删除叶子节点，
删除叶子节点：
1.删除叶子节点后，不影响平衡，直接删除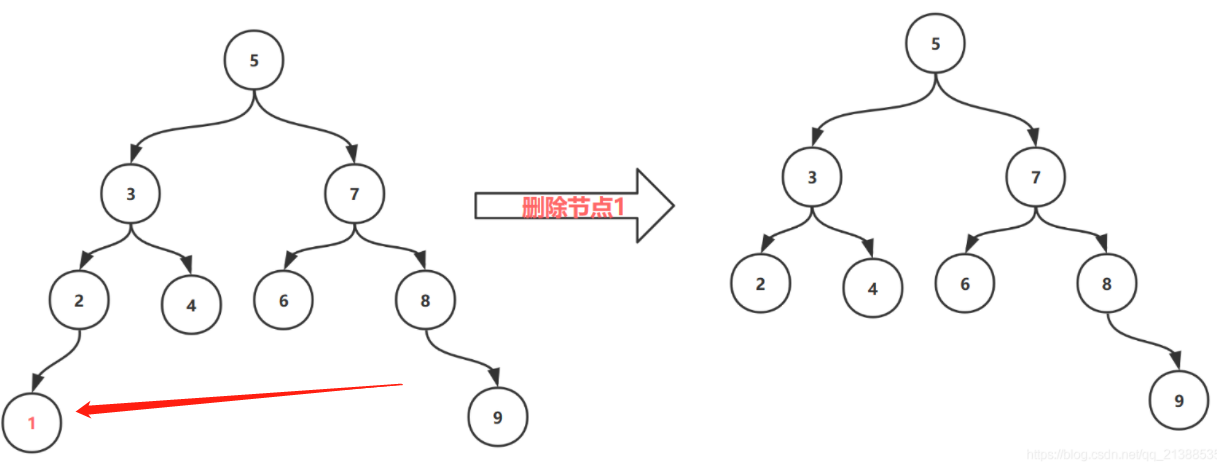

2.删除叶子节点后，影响平衡
将不平衡子树进行旋转处理，需要判断是左旋还是右旋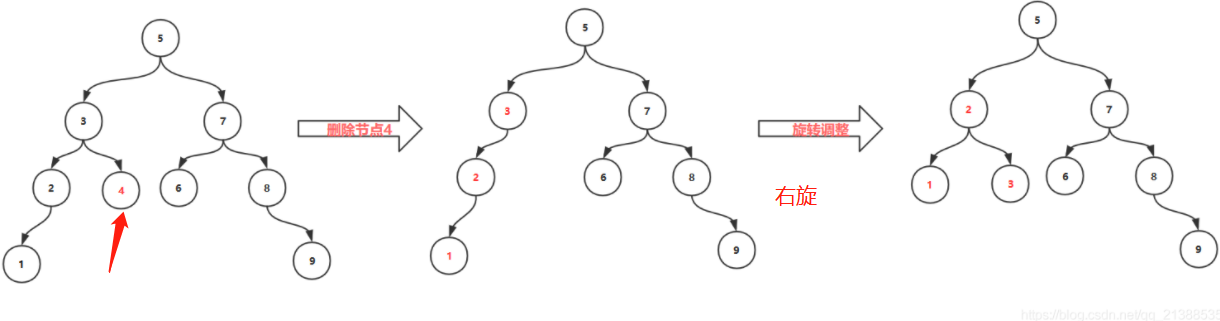

删除非叶子节点：
这个需要先知道什么是前驱节点跟后驱节点
前驱节点：在中序遍历中，一个节点的前驱结点，先找到该节点的左孩子节点，再找左孩子节点的最后一个右孩子节点。向左走一步，然后向右走到头。最后一个右孩子节点即为前驱节点
后驱节点：在中序遍历中，一个节点的后继结点，先找到该节点的右孩子节点，再找右孩子节点的最后一个左孩子节点。向右走一步，然后向左走到头。最后一个左孩子节点即为前驱节点
1.删除非叶子节点，该节点只有左孩子
操作：该节点的值替换为左孩子节点的值，然后删除左孩子节点（执行删除叶子节点的操作）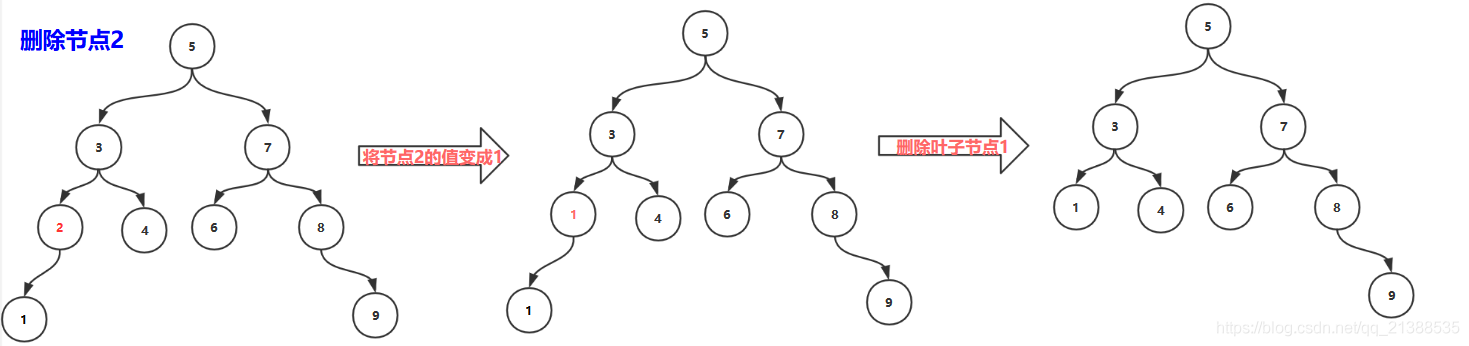

2.删除非叶子节点，该节点只有右孩子
操作：该节点的值替换为右孩子节点的值，然后删除右孩子节点（执行删除叶子节点的操作）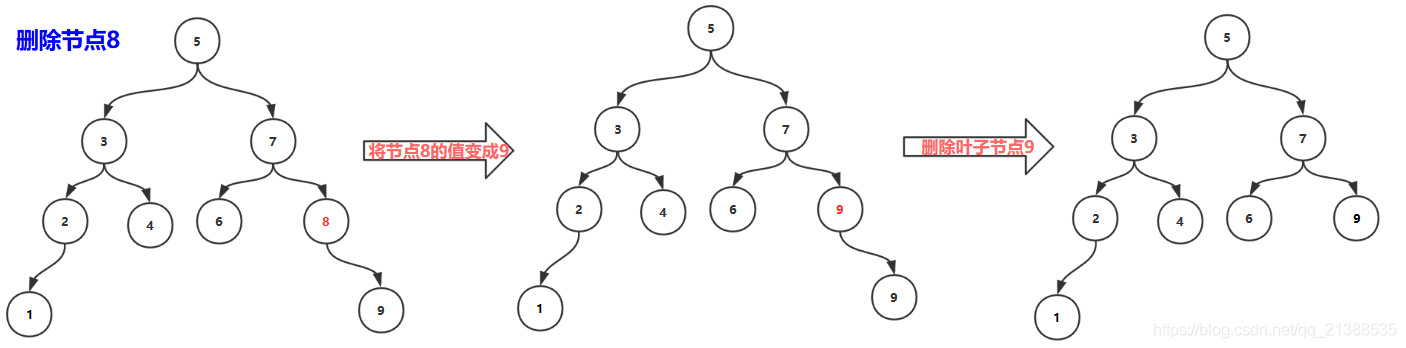

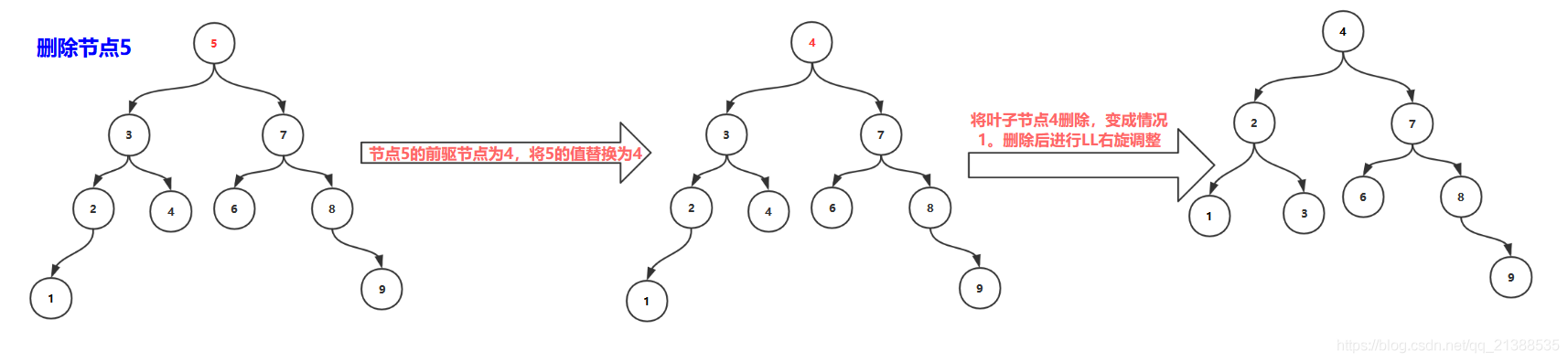
3.删除非叶子节点，该节点既有左孩子，又有右孩子
操作：
该节点的值替换为该节点的前驱节点（或者后继节点），
然后删除前驱节点（或者后继节点），此刻就变成了删除只有一个节点或者而样子节点的操作了
执行删除叶子节点或者只有一个节点的操作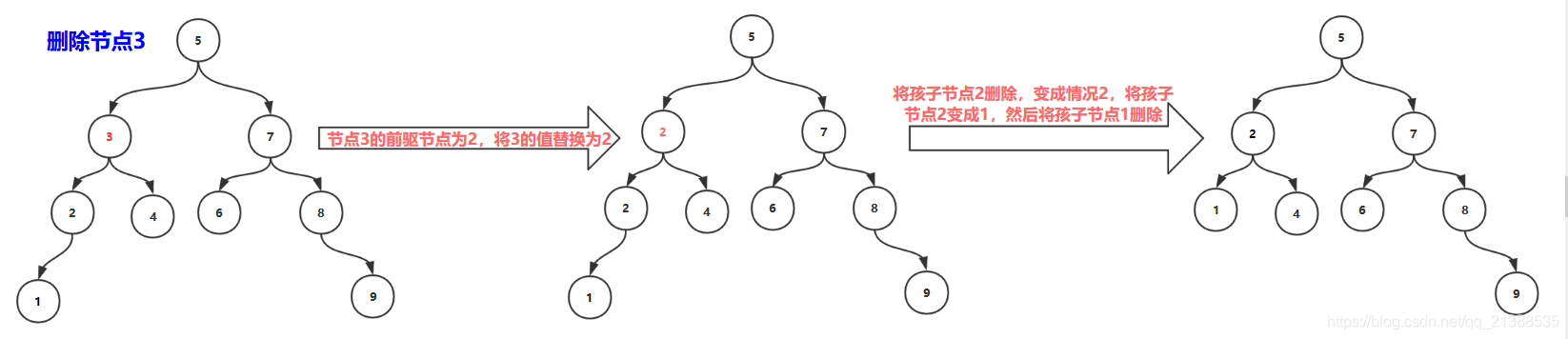


总结
| 描述 | 旋转方式 |
| 删除叶子结点 | 直接删除，判断平衡，旋转操作，然后依次向上调整为AVL树 |
| 删除非叶子节点，该节点只有左孩子 | 该节点的值替换为左孩子节点的值，然后删除左孩子节点|
| 删除非叶子节点，该节点只有右孩子 | 该节点的值替换为右孩子节点的值，然后删除右孩子节点|
| 删除非叶子节点，该节点既有左孩子，又有右孩子 | 该节点的值替换为该节点的前驱节点（或者后继节点），然后删除前驱节点（或者后继节点） |