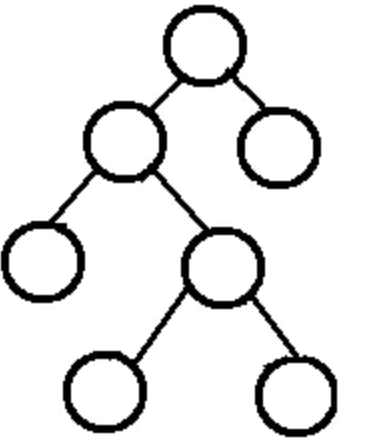
每个节点至多拥有两颗子树（即二叉树中不存在度大于2的节点），并且，二叉树的子树由左右之分起次序不能颠倒，常用来实现二叉查找树和二叉堆

性质：

1. 若二叉树的层次从0开始，则在二叉树的第i层之多由2^i个节点（i>=0）
   2. 高度为k的二叉树最多由2^(k+1)-1个节点，（k>=-1）(空树的高度为-1)
   3. 对于任何一棵二叉树如果其叶子节点（度为0）数为m，度为2 的节点数为n ，则m=n+1；

二叉树分为：完美二叉树（满二叉树），完全二叉树，完满二叉树
满二叉树（完美二叉树）
除了叶子节点之外的每一个节点，都有两个孩子，每一层（包含最后一层）都被完全填充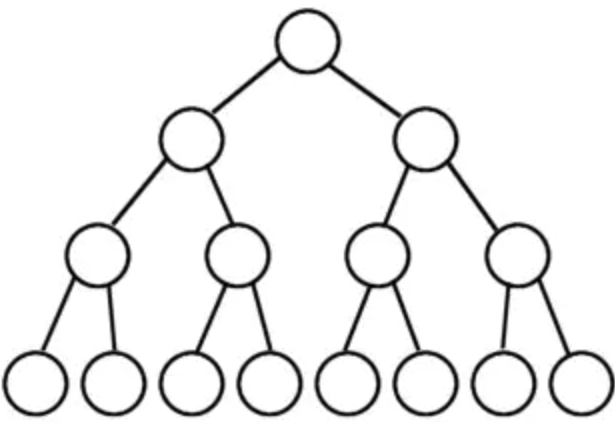

完全二叉树
除了最后一层外的其他每一层都被完全填充，并且所有节点都保持向左对齐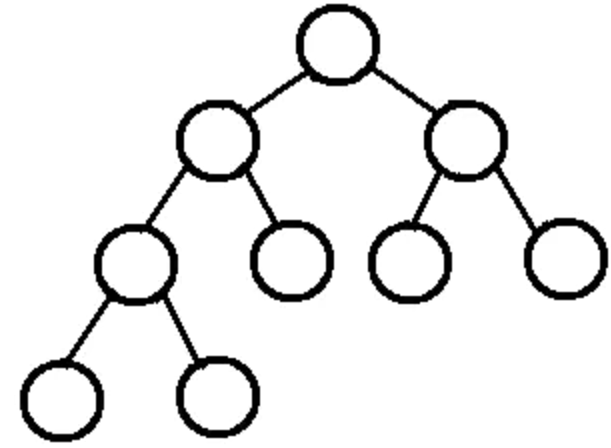

完满二叉树
除了叶子节点之外的每一个节点，都有两个孩子