一道非常典型的并查集应用题

集合的简化表示

1. 未简化的表示方法

  1. typedef struct{    /*数组类型:结构体*/
  2.     ElementType Data;    /*数据域Data*/
  3.     int Parent;        /*表示父结点位置的指针Parent*/
  4. } SetType;
  6. int Find(SetType S[], ElementType X){
  7.     int i;
  8.     for(i=0 ; i<MaxSize && S[i].Data != X ; i++);    /*此行目的:想知道元素属于哪个集合的线性扫描*/
  9.                 /*这样写非常浪费时间,最坏情况为O(n^2)*/
  10.     if(i>=MaxSize)    return -1;
  11.     for(; S[i].Parent >= 0 ; i=S[i].Parent);
  12.     return i;
  13. }

2. 化简思路

※ 任何有限集合的 N 个元素都可以被一一映射为整数 0 ~ N-1 ,
此处想法是 , 把集合中的每个元素直接用在数组里的下标来代表 , 只定义一个整型数组就可以表示集合了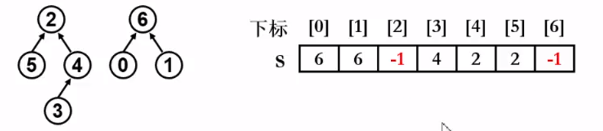
image.png
集合数 = 上图数组中 -1 的个数

3. 简化表示

  1. typedef int ElementType;    /*默认元素可以用非负整数表示*/
  2. typedef int SetNamel        /*默认用根结点的下标作为集合名称*/
  3. typedef ElementType SetType[MaxSize];
  5. SetName Find( SetType S, ElementType X){
  6.     /*默认集合元素全部初始化为-1*/
  7.     for( ; S[X]>=0 ; X=S[X]);    /*查找X在哪个集合*/
  8.     return X;
  9. }
  11. void Union(SetType S, SetName Root1, SetName Root2){
  12.     /*这里默认Root1和Root2是不同集合的根结点*/
  13.     S[Root2] = Root1;
  14. }

题意理解

题目 : 

  1. 输入样例1:
  2. 5                                            /*有5台计算机*/
  3. C 3 2                                    /*C表示Check,查看2和3之间有没有连通(不连通,输出no)*/
  4. I 3 2                                    /*I表示添加网线,在2和3之间加网线使其连通*/
  5. C 1 5                                    /*查看1和5之间是否连通(不连通,输出no)*/
  6. I 4 5                                    /*在4和5之间加网线使其连通*/
  7. I 2 4                                    /*在4和2之间加网线使其连通*/
  8. C 3 5                                    /*查看3和5之间是否连通(连通,输出yes)*/
  9. S                                            /*所有输入结束,对整个网络进行判断:一共有几个连通集*/
  10.                                             /*输出:There are 2 components*/
输入样例2:
5                                            /*有5台计算机*/
C 3 2                                    /*C表示Check,查看2和3之间有没有连通(不连通,输出no)*/
I 3 2                                    /*I表示添加网线,在2和3之间加网线使其连通*/
C 1 5                                    /*查看1和5之间是否连通(不连通,输出no)*/
I 4 5                                    /*在4和5之间加网线使其连通*/
I 2 4                                    /*在4和2之间加网线使其连通*/
C 3 5                                    /*查看3和5之间是否连通(连通,输出yes)*/
I 1 3
C 1 5
S                                            /*输出:The network is connected */

代码

1. 程序框架搭建

int main () {
初始化集合;
do {
读入一条指令; (C 1 5)
处理指令;
} while (没结束) ;
return 0;
}

int main(){
    SetType S;
    int n;
    char in;
    /*初始化集合:①读入元素个数②初始化*/
    scanf("%d\n",&n);
    Initialization(S,n);
    do{
        scanf("%c",&in);
        switch(in){
            case 'I' : Input_connection(S);break;            /*Input_connection:Union(Find)*/
            case 'C' : Check_connection(S);break;            /*Check_connection:Find*/
            case 'S' : Check_network(S,n);break;            /*Check_network:数一下一共有几个集合*/
        }
    } while(in != 'S');
    return 0;
}

void Input_connection( SetType S){
    ElementType u,v;
    SetName Root1, Root2;
    scanf("%d %d\n",&u,&v);
    Root1 = Find(S,u-1);
    Root2 = Find(S,v-1);
    if(Root1 != Root2)
        Union(S, Root1, Root2);
}

void Check_connection(SetType S){
    ElementType u,v;
    SetName Root1, Root2;
    scanf("%d %d\n",&u, &v);
    Root1 = Find(S, u-1);
    Root2 = Find(S, v-1);        /*从这往上与Input函数一样*/
    if( Root1 == Root2 )
        printf("yes\n");
    else printf("no\n");
}

void Check_network(SetType S, int n){
    int i, counter = 0;
    for(i=0 ; i<n ; i++){
        if( S[i] <0 )    counter++;
    }
    if( counter == 1 )
        printf("The network is connected.\n");
    else
        prinf("There are &d components.\n", counter);
}

根据上面代码 , 可以看出运行效率主要取决于函数 Union 和 Find 的效率。

2. 简单实现

简单实现的话 , 运行速度很慢 , 在某些测试中会超时。

3. 按秩归并

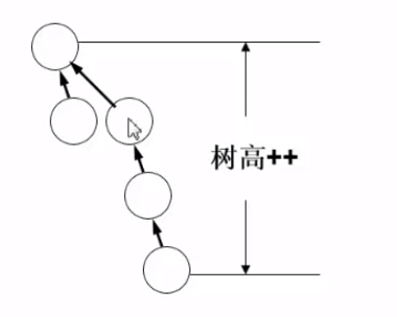
为什么需要按秩归并？

image.png
如上图 , 树会越长越高 , T(n) = O(n2)

不让树变高的方法

  • 把矮的树贴到高树上 (需要添加一行对哪颗树高哪颗树矮的判断)

    if (S[Root2] < S[Root1])        /*Root2高度 > Root1高度*/
  S[Root1] = Root2;
else{
  if(S[Root1]==S[Root2])    S[Root1]--;        /*两者等高,树高++*/
  S[Root2] = Root1;
}

  • 需要存储一下树的高度

image.png

树的高度存哪里 ?

S[Root] = -1 -> S[Root] = -树高 (仍初始化为 -1 )

另一种不让树变高的方法

比规模

  • 把小树贴到大树上 S[Root] = -元素个数