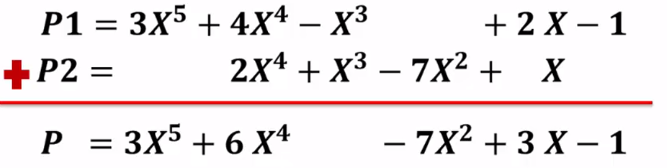多项式加法运算

基本思想

将两个多项式相加 , 主要思路是 : 相同指数的项系数相加 , 其余部分copy

image.png

实现

采用不带头结点的单向链表 , 按照指数递减的顺序排列各项

由分别表示系数和指数的两项以及指针构成一个元素

image.png

定义 :

  1. struct PolyNode{
  2.     int coef;     //系数
  3.     int expon;    //指数
  4.     struct PolyNode *lint;    指向下一个结点的指针
  5. };
  6. typedef struct PolyNode *Polynomial;
  7. Polynomial P1,P2;

算法思路

两个指针P1和P2分别指向这两个多项式第一个结点 , 不断循环 ;

  • P1->expon == P2->expon : 指数相等的情况下系数相加 , 若结果不为0 , 则作为结果多项式对应项的系数。 同时 , P1和P2都分别指向下一项 ;
  • P1->expon > P2->expon : 将P1的当前项存入结果多项式 , 并使P1指向下一项 ;
  • P1->expon < P2->expon : 将P2的当前项存入结果多项式 , 并使P2指向下一项 ;
  • 当某一多项式所有项都处理完时 , 将另一多项式的所有结点依次复制到结果多项式中去

image.png

实现

  1. Polynomial PolyAdd(Polynomial P1, Polynomial P2){
  2.     Polynomial front, rear, temp;
  3.     int sum;
  4.     rear = (Polynomial)malloc(sizeof(struct PolyNode));
  5.     front = rear;    //由front记录结果多项式链表头结点
  6.     while(P1 && P2)    //当两个多项式都有非零项待处理时
  7.         switch (Compare(P1->expon, P2->expon)){
  8.             case 1:
  9.                 Attach(P1->coef, P1->expon, &rear)
  10.                 P1 = P1->link;
  11.                 break;
  12.             case -1:
  13.                 Attach(P2->coef, P2->expon, &rear)
  14.                 P2 = P2->link;
  15.                 break;
  16.             case 0:
  17.                 sum = P1->coef + P2->coef;
  18.                 if(sum)Attach(sum, P1->expon, &rear);
  19.                 P1 = P1->link;
  20.                 P2 = P2->link;
  21.                 break  
  22.         }
  23.     /*将未处理完得另一个多项式的所有结点一次复制到结果多项式中去*/
  24.     for(;P1;P1 = P1->link)Attach(P1->coef, P1->expon. &rear);
  25.     for(;P2;P2 = P2->link)Attach(P2->coef, P2->expon. &rear);
  26.     rear->link = NULL;
  27.     temp = front;
  28.     front = front->link;    //令front指向结果多项式第一个非零项
  29.     free(temp);
  30.     return front;
  31. }

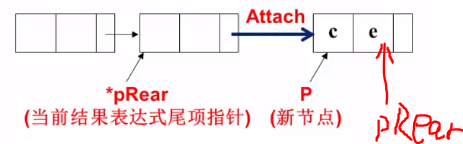
函数 Attach()

  1. void Attach(int c, int e, Polynomial *pRear){
  2.     Polynomial P;
  4.     P = (Polynomial)malloc(sizeof(struct PolyNode));
  5.     P->coef = c;    //对新结点赋值
  6.     P->expon = e;
  7.     P->link = NULL;
  8.     (*pRear)->link = P;
  9.     *pRear = P;        //修改pRear的值
  10. }

image.png

课件

2.4 应用实例—多项式加法运算.pdf