一 : 基本概念

如何在书架上摆放图书 ?

• 数据组织的时候与规模有关
  - 新书怎么插入?怎么找到指定书?

• 方法1: 随便放 (查找很麻烦)

• 方法2: 按字母顺序放 (二分查找, 插入麻烦)
• 方法3: 把书架划分区域 , 每个区域摆放固定类别 , 每种类别按字母顺序摆放 (二分查找 , 二分查找摆放)

什么是算法?

算法的特点 :

• 有限指令集
• 有输入或没有输入 , 一定有输出
• 一定在有限步骤之后终止
• 每一条指令必须 : 有目标无歧义 , 计算机能处理 , 不依赖于实现手段(语言等)

  //选择排序 伪代码
  void SelectionSort (int List[], int N)
  { /* 将N个整数List[0]...List[N-1]进行非递减排序*/
   for (i=0 ; i<N ; i++){
       MinPosition = ScanForMin( List, i, N-1);
   //从List[i]到List[N-1]中找最小元,并将其位置赋给MinPosition;
       Swap ( List[i], List[MinPosition]);
   //将未排序的部分的最小元换到有序部分的最后位置;
   } 
  }

什么是好的算法?

衡量算法的好坏 : 时间复杂度 T(n) 和 空间复杂度 S(n)

空间复杂度 S(n) : 占用存储单元的大小

void PrintN (int N){
    if (N) { //判断N不为0时递归执行以下语句
        PrintN( N-1 );
        printf("%d\n", N);
    }
    return;
}

由于递归调用 , 会事先存储变量 , 导致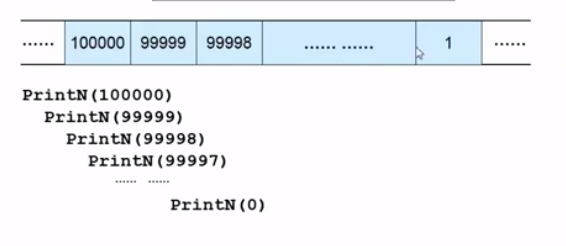

机器运算加减法的速度比乘除快很多 , 有加减乘除的时候加减的复杂度可以忽略不计

函数1：时间复杂度为

double f(int n, double a[], double x){
    int i;
    double p = a[0];
    for ( i = 1 ; i <= n ; i++ ) //执行n次
        p += (a[i] * pow(x, i)); //pow（）- x的i次方，执行i-1次
        // 一共执行 (1+2+...+n)=(n平方+n)/2 次乘法
    return p;
}

函数2：时间复杂度为

double f(int n, double a[], double x){
    int i;
    double p = a[n];
    for ( i = 1 ; i > 0 ; i-- )
        p = (a[i-1] + x * p); //一共执行n次乘法
    return p;
}

关注算法效率的两种复杂度

• 最坏情况复杂度 （易）
• 平均复杂度 （难）

复杂度的渐进表示法

• —— 表示存在常数 使得当 时有
  (能找到的、最小的上界)
• —— 表示存在常数 使得当 时有
  (能找到的、最大的下界)
  

输入规模

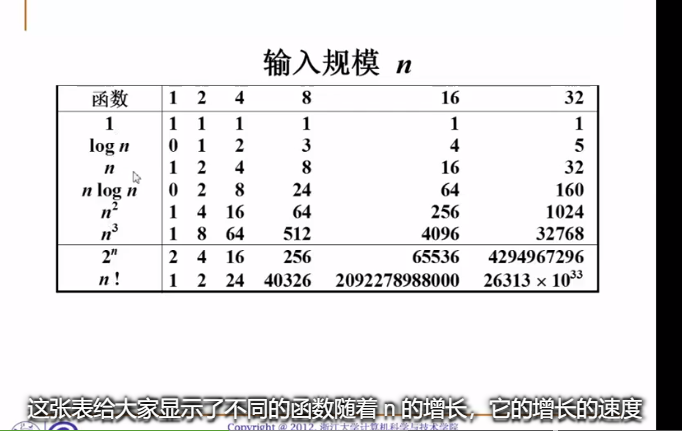
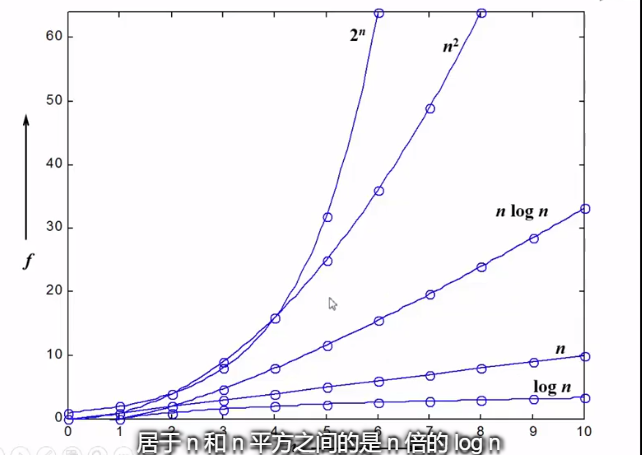
明显，当 时有复杂度为 。

复杂度分析

1. 若有两段算法分别由复杂度 和 ，则有
   

   //和为两个上界中比较大的那个
   //乘积为两个上界的乘积

2. 若 是关于 的 阶多项式，那么 //最大的上界，其他可以忽略不计

1. 一个 for 循环的时间复杂度等于 循环次数循环体代码的复杂度

1. if-else 结构的复杂度取决于 if 的条件判断复杂度和两个分支部分的复杂度，总体复杂度取三者中最大

实例：最大子列和问题

Q：给定个整数的序列，求函数 的最大值

算法1 : 暴力求解

直接求出所有的连续子列和，然后选最大的那个

int MaxSubseqSum1( int A[], int N ){  /* 输入整数数列A和整数数列里元素的个数N */
    int ThisSum, MaxSum = 0;
    int i, j, k;
    for( i = 0; i < N ; i++ ){  /* i是子列左端位置，从A[i]开始 */
        for( j = i; j < N; j++ ){ /* j是子列右端位置，到A[j]结束 */
            ThisSum = 0; /* ThisSum是从A[i]到A[j]的子列和 */
            for( k = i; k <= j; k++)
                ThisSum += A[k];
            if(ThisSum > MaxSum)   /* 如果刚得到的这个子列和更大 */
                MaxSum = ThisSum;    /* 则更新结果 */
        } /* j循环结束 */
    } /* i循环结束 */
    return MaxSum;
}

复杂度为 : (有三层嵌套的 for 循环 : (0到n第一层) (i到n第二层) (i到j第三层))
性能很差

算法2 : 暴力求解优化

int MaxSubseqSum2( int A[], int N ){  /* 输入整数数列A和整数数列里元素的个数N */
    int ThisSum, MaxSum = 0;
    int i, j, k;
    for( i = 0; i < N ; i++ ){  /* i是子列左端位置，从A[i]开始 */
        for( j = i; j < N; j++ ){ /* j是子列右端位置，到A[j]结束 */
            ThisSum = 0; /* ThisSum是从A[i]到A[j]的子列和 */
                ThisSum += A[j];
            /* 对于相同的i不同的j,只要在j-1次循环的基础上累加1项即可*/
            if(ThisSum > MaxSum)   /* 如果刚得到的这个子列和更大 */
                MaxSum = ThisSum;    /* 则更新结果 */
        } /* j循环结束 */
    } /* i循环结束 */
    return MaxSum;
}

复杂度为 : (有两层层嵌套的 for 循环 : (0到n第一层) * (i到j第二层))

把复杂度为n的算法改进成nlogn是比较容易而且效率提升了很多

算法3 : 分治算法

(把复杂的问题切分成小块 , 分别解决 , 再把结果合并 , 分而治之)
一分为二 ; 递归解决左半边 ; 递归解决右半边 ;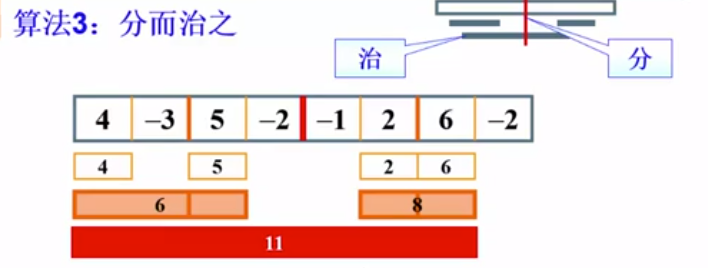

复杂度 (分析递归) :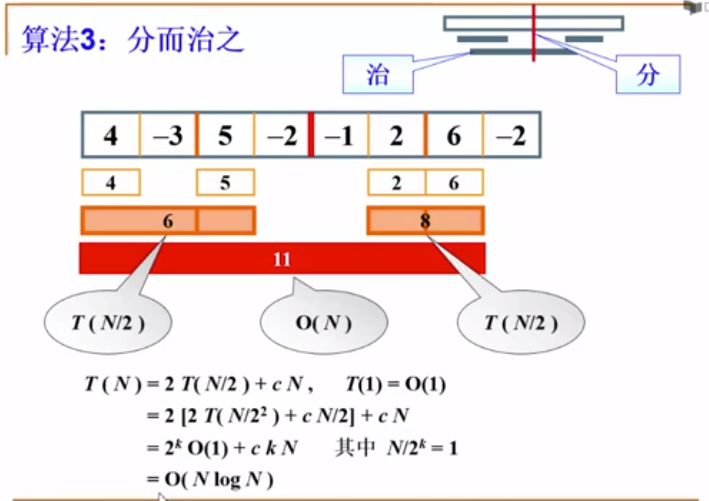

不是最快的算法 , 更快的算法 : 在线处理算法

算法4 : 在线处理

int MaxSubseqSum2( int A[], int N ){  /* 输入整数数列A和整数数列里元素的个数N */
    int ThisSum, MaxSum;
    int i;
    ThisSum = MaxSum = 0
    for( i = 0; i < N ; i++ ){
        ThisSum += A[i]; /* 向右累加 */
        if(ThisSum > MaxSum)   /* 如果刚得到的这个子列和更大 */
                MaxSum = ThisSum;    /* 则更新结果 */
        else if( ThisSum < 0 ) /* 如果当前子列和为负*/
            ThisSum = 0;    /* 则不可能是后面部分增加,抛弃*/
    } 
    return MaxSum;
}

复杂度为 (可能得到的最快算法)
副作用 : 正确性不明显
“在线”指每输入一个数据就进行即时处理 , 在任何一个地方中止输入 , 算法都能正确给出当前的解