编码有多种方式 , 整数有二进制。用7位(加首位0=8位)进行计算机编码 , 但不同字符出现的频率不同 , 如果能用少位来对出现频率高的字符(用5位表示E等等) , 可以提高效率。即 , 已知字符出现的频率不同 , 怎样对其编码能使效率最高 ?

什么是哈夫曼树

例 : 将百分制成绩转换成五分制

判定树1

  1. if(score<60) grade = 1;         /*~60*/
  2. else if(score<70) grade = 2;    /*60~70*/
  3. else if(score<80) grade = 3;    /*70~80*/
  4. else if(score<90) grade = 4;    /*80~90*/
  5. else grade = 5;                    /*90~*/

上述规则对应一个判定树 :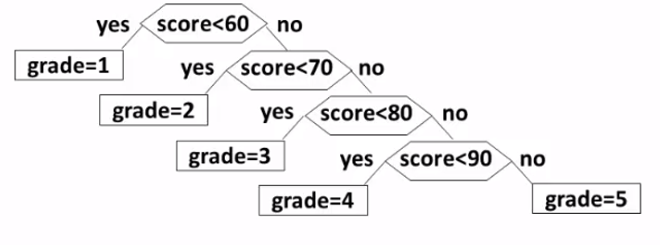
image.png
从上图可以看出 , 60分以下时只需要做一次判断就可以得出结果 , 而90分以上时需要做 4 次判断才能得出结果。如果本次考试大部分人都得了90分以上 , 则大部分人都需要做 4 次判断 , 效率极低。

如果考虑学生成绩分布的概率 :
image.png
则查找效率为 : 0.05×1(次判断)+0.15×2+0.4×3+0.3×4+0.1×4 = 3.15 (平均查找次数)

判定树2

如果修改判定树为先对80分进行判断 :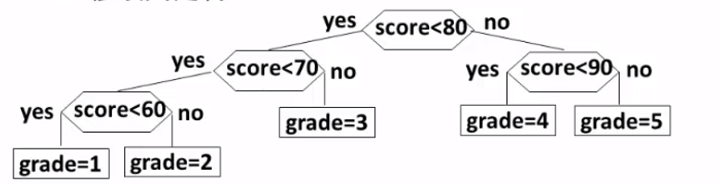
image.png
修改程序为 :

if(score<80){
    if(score<70)
        if(score<60) grade=1;
        else grade=2;
}else if(score<90)    grade=4;
else grade=5;

则查找效率为 : 0.05×3+0.15×3+0.4×2+0.3×2+0.1×2 = 2.2 (平均查找次数)

发现问题

如何根据结点的不同的查找频率来构造更有效的搜索树? —— 哈夫曼树

哈夫曼树的定义

带权路径长度 (WPL) : 设二叉树有 n 个叶子结点 , 每个叶子结点带有权值 w**k , 从根结点到每个叶子结点的长度为 lk **, 则每个叶子结点的带权路径长度之和就是 : 三 : 树(下) - (2)哈夫曼树与哈夫曼编码 - 图4

最优二叉树或哈夫曼树 : WPL最小的二叉树

示例

有五个叶子结点 , 他们的权值为 {1, 2, 3, 4, 5} , 用此权值序列可以构造出形状不同的多个二叉树

可以构造出不同的判别树 :
(1) 把权值高的放在前面
WPL = 5×1 + 4×2 + 3×3 + 2×4 + 1×4 = 34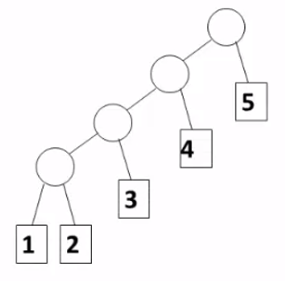
image.png
(2) 把权值高的放在后面
WPL = 1×1 + 2×2 + 3×3 + 4×4 + 5×4 = 50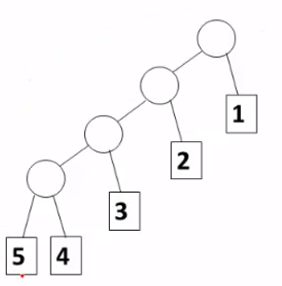
image.png
(3) 平衡 :
WPL = 3×1 + 3×2 + 2×3 + 2×4 + 2×5 = 33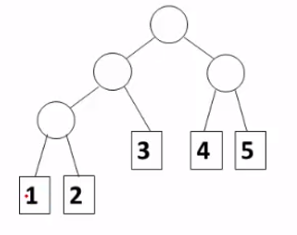
image.png

哈夫曼树的构造

※ 每次把权值最小的两棵二叉树合并

合并权值为 {1, 2, 3, 4, 5} 的哈夫曼树 ：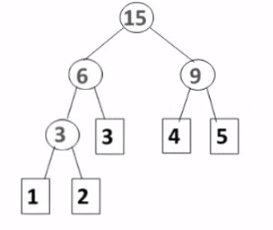
image.png
步骤 :
(1) 挑两个权值最小的元素为左右子结点 , 构造一个父结点 , 其权重为两元素权重之和
(2) 包括上述父结点的权重 , 与其他权重合在一块 , 挑出两个权值最小的元素构造父结点
(3) 重复(2)
(4) 当剩下最后两个元素时 直接合并

哈夫曼树的实现

typedef struct TreeNode *HuffmanTree;
struct TreeNode{
    int Weight;
    HuffmanTree Left,Right;
}
HuffmanTree Huffman( MinHeap H ){
    /*假设H->Size个权值已经存在H->Elements[]->Weight里*/
    int i; HuffmanTree T;
    BuildMinHeap(H);    /*将H->Elements[]按权值调整为最小堆*/
    for( i=1 ; i< H->Size ; i++){    /*做H->Size-1次合并*/
        T = malloc(sizeof(struct TreeNode));    /*建立新结点*/
        T->Left = DeleteMin(H);        /*从最小堆中删除一个结点,作为新T的左子结点*/
        T->Right = DeleteMin(H);        /*从最小堆中删除一个结点,作为新T的左子结点*/
        T->Weight = T->Left->Weight+T->Right->Weight;    /*计算新权值*/
        Insert(H,T);        /*将新T插入最小堆*/
    }
    T = DeleteMin(H);
    return T;
}                         /*整体复杂度 O(nlogn)*/

程序中最主要解决的问题 : 如何选取两个最小的元素 ? —— **利用堆

哈夫曼树的特点

※ 没有度为 1 的结点 (因为构造时开始就是两个结点合并)
※ n 个叶子结点的哈夫曼树共有 2n-1 个结点
image.png
※ 哈夫曼树的任意非叶结点的左右子树交换后仍是哈夫曼树

问题 : 对同一组权值 { w** ,w** ,…… ,w**}** , 是否存在不同构的两颗哈夫曼树呢 ?
※ 可能。但不同构的两颗哈夫曼树 带权路径长度 (WPL) (最优化后) 仍然相同。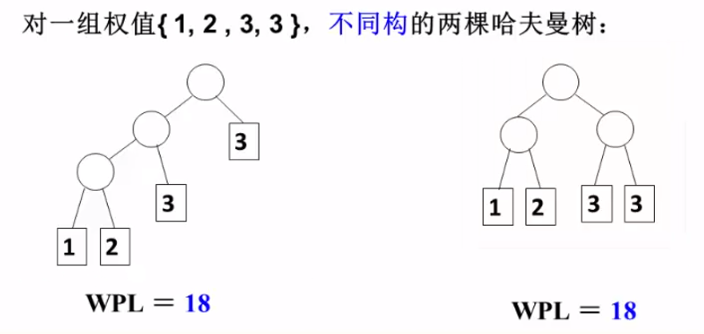
image.png

哈夫曼编码

示例

给定一段字符串 , 如何对字符进行编码 , 使得该字符串的编码存储空间最少 ?

例题

假设有一段文本 , 包含 58 个字符 , 并由以下 7 个字符构成 : a、e、i、s、t、空格(sp)、换行(nl) , 这 7 个字符出现的次数不同。如何对这 7 个字符进行编码 , 使得总编码空间最少 ?

思路

(1) 用等长 ASCII编码 : 58×8 = 464位
(2) 用等长 3 位编码 : 58×3 = 174位
(3) 不等长编码 : 出现频率高的字符用的编码短 , 低的编码长些

怎么进行不等长编码?

假设 : a:1 e:0 s:10 t:11 , 问题 : 1011解码有很多种方式 , 比如aeaa或aet或st , 有二义性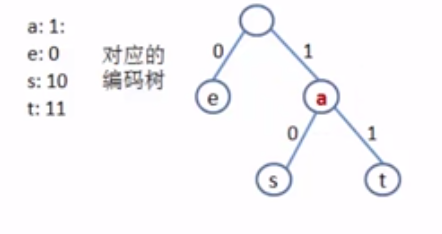
image.png 当编码(a)有一个结点出现在非叶结点上的时候 就会出现前缀

只要编码加入前缀码prefix code就可以削除二义性 !
( 条件 : 任何字符的编码都不是另一字符编码的前缀 )

如何加入前缀码? —— 用二叉树

  • 左右分支 : 0 / 1
  • 所有字符只在叶结点上 (避免前缀出现)

假设四个字符的频率 : a:4次 u:1次 x:2次 z:1次 , 则等长码构造出的二叉树为 : a:00 u:01 x:10 z:11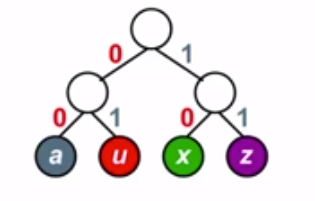
image.pngimage.png
不等长码构造出的哈夫曼树为 : a:0 x:10 u:110 z:111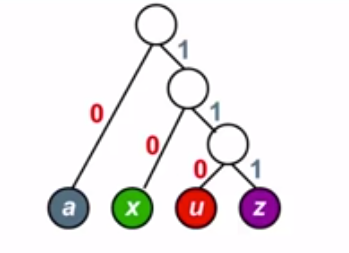
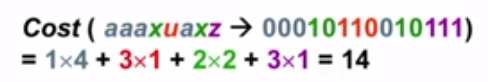
image.pngimage.png

回到例题

频率为 : image.png
构造哈夫曼树 :
挑两个最小的合并形成新的权值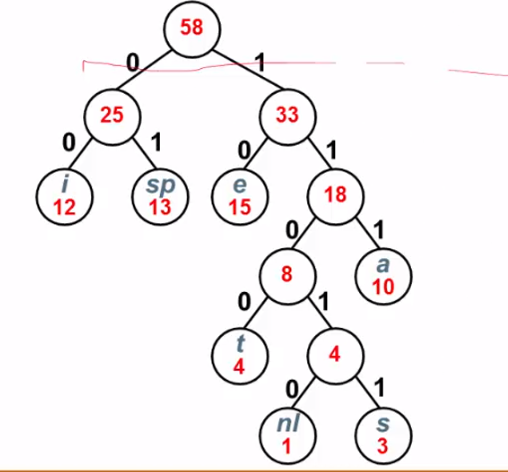
image.png 对应的编码 : image.png
Cost = 3(a编码的位数)×10+ 2(e编码的位数)×15 + 2×12 + 5×3 + 4×4 + 2×13 + 5×1 = 146

讨论 : 判别是否是前缀码的算法

字典树，前缀树，tire tree算法实现

课件

5.2哈夫曼树与哈夫曼编码.pdf