题意理解

将一系列的给定数字 , 插入到一个初始为空的小顶堆(最小堆) H[]。
随后对任意给定的下标 i , 打印从 H[i] 到根结点的路径。(不超过1000个给定数字)

**###输入样例 : **
5 3 (5个数据的最小堆 , 进行3次查询)
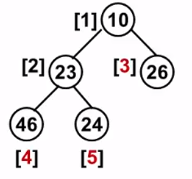
46 23 26 24 10 (按顺序插入的5个数据)
5 4 3 (需要查询的数据 , 用下标表示)

比如 : 第一个是5 , 表示 H[5] = 24 , 从24经过23到10的路径 -> 24 23 10 第二个是4 , 表示 H[4] = 46 , 从46经过23到10的路径 -> 46 23 10 第三个是3 , 表示 H[3] = 26 , 从26到10的路径 -> 26 10

**###输出样例 :**
24 23 10
46 23 10
26 10

插入后构成的最小堆 :
image.png

解题

1. 堆的表示及操作

堆是一种按一定顺序组织的完全二叉树 , 堆可以用数组来直截了当的表示。
对于完全二叉树 (此处是堆) 的任何一个结点 **i** , 其父结点为 **i/2** , 左儿子为 **2i** , 右儿子为 **2i+1**

  1. /*堆的表示分为,定义数组+表示当前堆大小的size*/
  2. #define MAXN 1001
  3. #define MINH -10001
  4. int H[MAXN], size;    /*size表示堆的大小*/
  5. void Create(){        /*构建对堆进行初始化的函数*/
  6.     size = 0;
  7.     H[0] = MINH;    /*设置哨兵*/
  8. }
  10. /*插入操作,把在最底层的插入元素一层层与其父结点比较,到根结点为止*/
  11. void Insert( int X ){
  12.     /*将X插入H。这里省略检查堆是否已满的代码*/
  13.     int i;
  14.     for(i=++size ; H[i/2]>X ; i/=2)    /*i=size时是最大位置*/
  15.         /*此处因为之前有了哨兵H[0]的存在,就不需要判别比较元素的下标i有没有越界*/
  16.         H[i] = H[i/2];
  17.     H[i] = X;
  18. }

2. 主程序

思路 :
int main(){
※ 读入n和m
※ 根据输入序列建立n个元素的堆
※ 对于要求的m个位置分别打印从H[m]到根结点的路径

return 0;
}

n表示元素个数(上例为第一行的5) , m表示查询次数(上例为第一行的3)

int main(){
    int n,m,x,i,j;

    scanf("%d%d",&n,&m);
    Create();    /*堆初始化*/
    for(i=0 ; i<n ; i++){    /*以逐个插入方式建堆*/
        scanf("%d",&x);
        Insert(x);
    }    /*完成读入并建堆*/
    for(i=0 ; i<m ; i++){
        scanf("%d",&j);
        printf("%d",H[j]);
        while(j>1){        /*沿根方向输出各结点*/
            j/=2;
            printf("%d",H[j]);
        }
    } 
    return 0;
}