什么是队列

Queue : 具有一定操作约束的线性表 (只能在一端插入 , 而在另一端删除)

堆栈的插入和删除只能在同一端进行

• 数据插入 : 入队 (AddQ)
• 数据删除 : 出队 (DeleteQ)
• 先进先出 : FIFO

**

队列的抽象数据类型描述

操作集

1. Queue CreateQueue( int MaxSize ) : 生成长度为MaxSize的空队列
2. int IsFullQ( Queue Q, int MaxSize ) : 判断队列Q是否已满
3. void AddQ( Queue Q, ElementType item) : 将数据元素item插入队列Q中
4. int IsEmptyQ( Queue Q ) : 判断队列Q是否为空
5. ElementType DeleteQ( Queue Q ) : 将队头数据元素从队列中删除并返回

队列的顺序存储实现

通常由一个一维数组和一个记录队列头元素位置的变量 front 以及一个记录队列尾元素位置的变量 rear 组成

堆栈是一个数组和一个Top

定义 :

#define MaxSize<储存数据元素的最大个数>
struct QNode{
    ElementType Data[MaxSize];
    int rear;
    int front;
};
typedef struct QNode *Queue;

• 开始时 , 队列为空 , 队头变量front 和队尾变量 rear 都指向 -1
• 向里面添加 Job 1 (AddQ Job 1) , 此时 rear 指向 Job 1 , 在往后添加Job时指向当前添加的Job

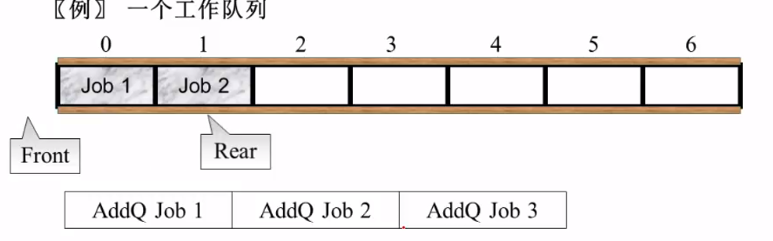
• 删除元素 Job 1 , 此时 front 指向 0 的位置 (原来 Job 1 的位置)

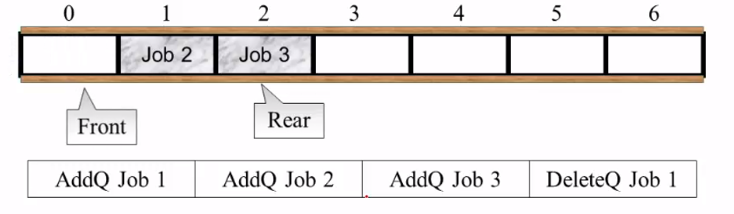
• 总的来说 添加一个元素时 rear ++ ; 删除一个元素时 front ++ ;

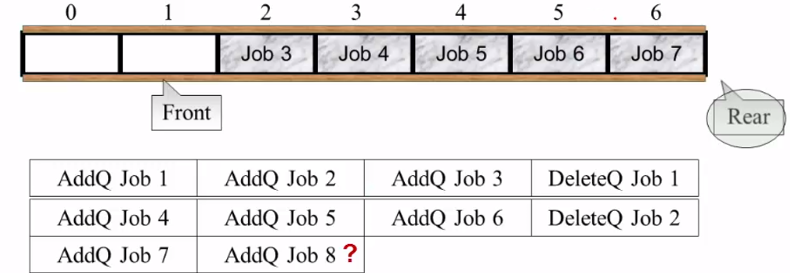
上图情况发生时 , 队尾已经满了没法再添加 , 但队头还有空位置 , 可以将 rear 指向 0 的位置构成循环队列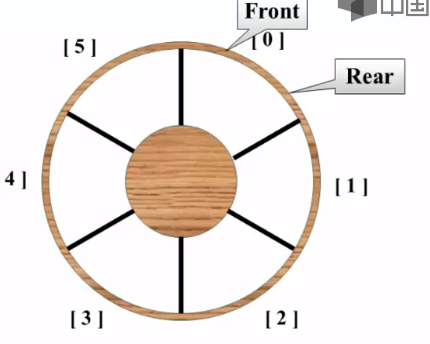

队列空 : **front == rear

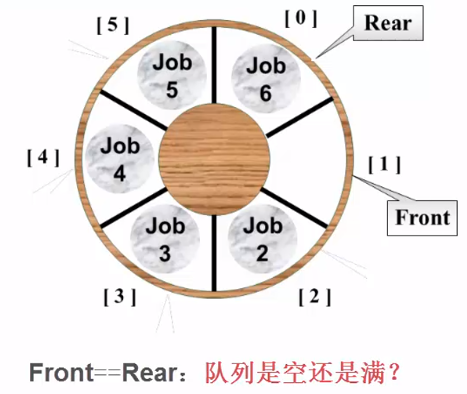
此时出现矛盾 : 0,1,2,3,4,5 一共6个相对距离没办法表示出 (0到6) 一共7个相对状态
有两种解决方案 :
(1) 使用额外标记 : Size 或者 Tag域 (1或0 , 对应 front==rear 时的空或满)
(2) 仅使用 n-1 个数组空间

操作

(1) 入队列

void AddQ(Queue PtrQ, ElementType item){
    if((PtrQ->rear +1)% MaxSize == PtrQ ->front){ /*判断队列是否满,rear+1=最大元素个数,用求余*/
        printf("队列满");return;}
    PtrQ->rear = (PtrQ->rear+1)% MaxSize; /*最大rear数用求余*/
    PtrQ->Data[PtrQ->rear]=item;
}

(2) 出队列

ElementType DeleteQ(Queue PtrQ){
    if(PtrQ->front == PtrQ->rear){ /*front和rear是否相等 判断出队列是否为空*/
        printf("队列空");return ERROR;
    }else{
        PtrQ->front = (PtrQ->front+1)% MaxSize;
        return PtrQ->Data[PtrQ->front];
    }
}

队列的链式存储实现

front

定义 :

struct Node{
    ElementType Data;
    struct Node *Next;
};
struct QNode{ /*链队列结构*/
    struct Node *rear; /*指向队尾结点*/
    struct Node *front;/*指向队头结点*/
};
typedef struct QNode *Queue;
Queue PtrQ;

不带头结点的链式队列出队操作的一个示例 :

ElementType DeleteQ(Queue PtrQ){
    struct Node *FrontCell;
    ElementType FrontElem;
    if(PtrQ->front == NULL){  /*根据上图,front是NULL的时候就是队列空*/
        printf("队列空");return ERROR;
    }
    FrontCell = PtrQ->front;
    if(PtrQ->front == PtrQ->rear)        /*若队列中只有一个元素1`2*/
        PtrQ->front = PtrQ->rear = NULL;    /*删除后队列置为空*/
    else
        PtrQ->front = PtrQ->front->Next;
    FrontElem = FrontCell->Data;
    free(FrontCell);        /*释放被删除的结点空间*/
    return FrontElem;
}

同样可以实现入队操作

小测验

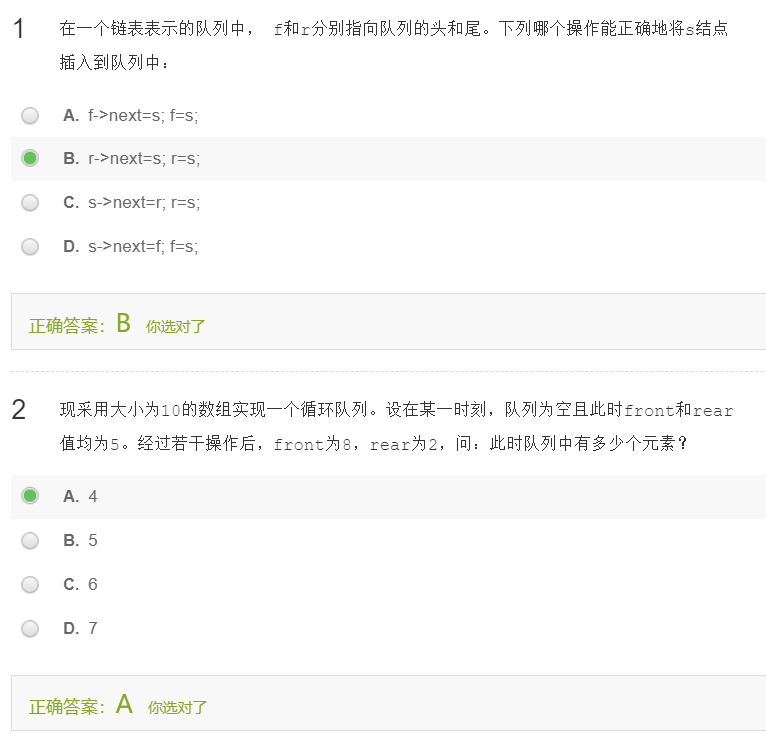
讨论

如何用两个堆栈模拟实现一个队列?
如果这两个堆栈的容量分别是m和n（m>n)，你的方法能保证的队列容量是多少？

堆栈是先进后出，队列是先进先出，用两个堆栈倒腾两次正好把顺序反过来就能实现队列的操作。
一个堆栈用来出队（可以叫stackPop），一个堆栈用来入队(可以叫stackPush)。
要实现先进先出，要把数据从stachPush中倒腾到stackPop中，倒腾的时候，必须保证两点：
(1). stackPush往stackPop倒腾的时候，必须一次把stackPush的时候全部弹出去。
(2).stackPop中有数据的时候，不能倒腾。
入队很简单，直接push到stackPop中。 出队时stackPop里没有元素的话，就把stackPush里面的元素都倒腾过来，然后出去一个就好了。出队时如果stackPop里有元素，就直接出去一个就ok。

课件

2.3队列.pdf

C语言实现 - 队列的定义和操作(顺序_数组)

typedef int Position;
struct QNode {
    ElementType *Data;     /* 存储元素的数组 */
    Position Front, Rear;  /* 队列的头、尾指针 */
    int MaxSize;           /* 队列最大容量 */
};
typedef struct QNode *Queue;
Queue CreateQueue( int MaxSize )
{
    Queue Q = (Queue)malloc(sizeof(struct QNode));
    Q->Data = (ElementType *)malloc(MaxSize * sizeof(ElementType));
    Q->Front = Q->Rear = 0;
    Q->MaxSize = MaxSize;
    return Q;
}
bool IsFull( Queue Q )
{
    return ((Q->Rear+1)%Q->MaxSize == Q->Front);
}
bool AddQ( Queue Q, ElementType X )
{
    if ( IsFull(Q) ) {
        printf("队列满");
        return false;
    }
    else {
        Q->Rear = (Q->Rear+1)%Q->MaxSize;
        Q->Data[Q->Rear] = X;
        return true;
    }
}
bool IsEmpty( Queue Q )
{
    return (Q->Front == Q->Rear);
}
ElementType DeleteQ( Queue Q )
{
    if ( IsEmpty(Q) ) { 
        printf("队列空");
        return ERROR;
    }
    else  {
        Q->Front =(Q->Front+1)%Q->MaxSize;
        return  Q->Data[Q->Front];
    }
}

C语言实现 - 队列的定义和操作(链式_链表)

typedef struct Node *PtrToNode;
struct Node { /* 队列中的结点 */
    ElementType Data;
    PtrToNode Next;
};
typedef PtrToNode Position;
struct QNode {
    Position Front, Rear;  /* 队列的头、尾指针 */
    int MaxSize;           /* 队列最大容量 */
};
typedef struct QNode *Queue;
bool IsEmpty( Queue Q )
{
    return ( Q->Front == NULL);
}
ElementType DeleteQ( Queue Q )
{
    Position FrontCell; 
    ElementType FrontElem;
    if  ( IsEmpty(Q) ) {
        printf("队列空");
        return ERROR;
    }
    else {
        FrontCell = Q->Front;
        if ( Q->Front == Q->Rear ) /* 若队列只有一个元素 */
            Q->Front = Q->Rear = NULL; /* 删除后队列置为空 */
        else                     
            Q->Front = Q->Front->Next;
        FrontElem = FrontCell->Data;
        free( FrontCell );  /* 释放被删除结点空间  */
        return  FrontElem;
    }
}