题目

设计函数分别求两个一元多项式的乘积与和 (变量只有一个)

已知两个多项式 :
(1) 二 : 线性结构 - (5)实例 : 多项式乘加 - 图1
(2) 二 : 线性结构 - (5)实例 : 多项式乘加 - 图2

多项式和 : 二 : 线性结构 - (5)实例 : 多项式乘加 - 图3 (项合并)
多项式乘积 : 二 : 线性结构 - (5)实例 : 多项式乘加 - 图4

样例

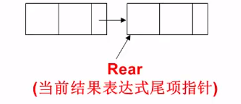
输入样例

4 3 4 -5 2 6 1 -2 0
3 5 20 -7 4 3 1

输出样例

15 23 -25 22 30 21 -10 20 -21 8 35 6 -33 5 14 4 -15 3 18 2 -6 1
5 20 -4 4 -5 2 9 1 -2 0

求解思路

多项式表示
数据结构设计
程序框架搭建
读入多项式
多项式相加
多项式相乘
多项式输出

1. 多项式表示

重点是 : 仅表示非零项
可以选择数组或链表

数据结构	数组	链表
特征	编程简单、调试容易	动态性强
	需要事先确定数组大小	编程略微复杂、调试比较困难

一种比较好的实现方法是 : 动态数组
(例子用链表实现)

2. 数据结构设计

typedef struct PolyNode *Polynomial;
struct PolyNode{
    int coef;
    int expon; 
    Polynomial link;
}; /*一个元素包含系数 指数和指针*/

3. 程序框架搭建

#整体框架
int main()
{
    读入多项式1
    读入多项式2
    乘法运算并输出
    加法运算并输出
    return 0;    
}

根据上述框架 , 确定了需要设计的函数都有 :

func(读取一个多项式)
func(两多项式相乘)
func(两多项式相加)
func(多项式输出)

据此 , 定义 main() 函数如下 :

int main()
{
    Polynomial P1,P2,PP,PS; //定义四个结点的指针
    P1 = ReadPoly();
    P2 = ReadPoly();
    PP = Mult( P1,P2 );
    PrintPoly( PP );
    PS = Add( P1,P2 );
    PrintPoly( PS );
    return 0;
}

4. 读入多项式

读入后的格式 : 4 3 4 -5 6 1 -2 0 (第一个4表示多项式的项数)

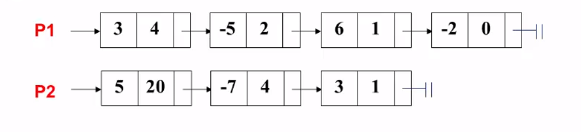
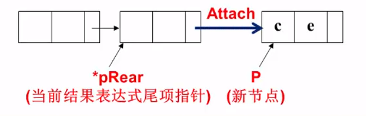
需要一个 rear 指针 , 表示当前结果表达式的尾项指针
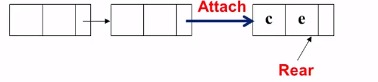
需要一个函数 Attach , 目的是把读取的c和e插入到新构造的结点中

Attach()

问题 : Rear的初值是?
处理方法1 : Rear初值为NULL (在Attach函数中根据Rear是否为NULL做不同处理) (因为Rear从第二项开始就不为 NULL)
处理方法2 : Rear指向一个空结点 (一开始指向空结点) (采用此方法)

void Attach( int c, int e, Polynomial *pRear)
{
    Polynomial P; /*当前传进来的是Polynomial类型的指针*/
    /*pRear是指针的指针*/
    P = (Polynomial)malloc(sizeof(struct PolyNode));
    P->coef = c ;
    P->expon = e;
    P->link = NULL;
    (*pRear)->link = P;
    *pRear = P;
}

读入多项式

Polynomial ReadPoly()
{
    Polynomial P, Rear, t;
    int c,e,N;
    scanf("%d",&N);
    P = (Polynomial)malloc(sizeof(struct PolyNode)); /*链表头空结点*/
    P->link = NULL;
    Rear = P;
    while (N--){
        scanf("%d %d",&c,&e);
        Attach(c,e,&Rear)        /*将当前项插入多项式尾部*/
    }
    t=P; P=P->link; free(t);    /*删除临时生成的头结点*/
    return P;
}

完成时的链表 :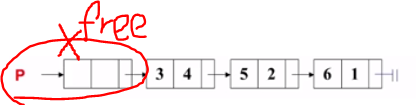

5. 多项式相加

流程 :

先判断 : 当t1 t2 都不空的时候 , 比较t1 t2 当前项的指数大小 (相等则系数相加)

6. 多项式相乘

方法 :

将乘法运算转换为加法运算
将P1当前项 (ci,ei) 乘P2多项式 , 再加到结果多项式里
```
while(t2){
 Attach(t1->coef * t2->coef, t1->expon + t2->expon, &Rear);
 t2 = t2->link;
}
```
逐项插入
将P1当前项 (c1_i,e1_i) 乘P2当前项 (c2_i,e2_i) , 并插入到结果多项式中 , 关键是找到插入位置
初始结果多项式可由P1第一项乘P2获得 (如上)

逐项插入

**

Polynomial Mult(Polynomial P1, Polynomial P2)
{
    Polynomial P, Rear, t1, t2, t;
    int c, e;

    if(!P1 || !P2) return NULL;

    t1 = P1; t2 = P2;
    P = (Polynomial)malloc(sizeof(struct PolyNode));P->link = NULL;
    Rear = P;
    while(t2){    /*先用P1的第1项乘以P2, 得到P*/
        Attach(t1->coef * t2->coef, t1->expon + t2->expon, &Rear);
        t2 = t2->link;
    }
    t1 = t1->link;

    while(t1){
        t2 = P2; Rear = P;
        while(t2){
            e = t1->expon + t2->expon;
            c = t1 ->coef * t2->coef;
            while(Rear->link && Rear->link->expon > e)
                Rear = Rear->link;
            if(Rear->link && Rear->link->expon == e){
                if(Rear->link->coef+c)
                    Rear->link->coef += c;
                else{
                    t= Rear->link;
                    Rear->link = t->link;
                    free(t);
                }
            }
            else{
                t=(Polynomial)malloc(sizeof(struct PolyNode));
                t->coef = c; t->expon = e;
                t->link = Rear->link;
                Rear->link = t; Rear = Rear->link;
            }
        }
    }
    t2 = P; P = P->link; free(t2);

    return P;
}

7. 多项式输出

相当于遍历一遍链表
基本框架 :

void PrintPoly(Polynomial P)
{/*输出多项式*/
    while(P){
        ...
            P = P->link
    }
}

实现 :

void PrintPoly(Polynomial P)
{/*输出多项式*/
    int flag = 0;     /*辅助调整输出格式*/
    if(!P){printf("0 0\n");return;}        /*多项式为空时*/
    while(P){
        if(!flag)
            flag = 1;
        else
            print(" ");
        printf("%d %d",P->coef, P->expon);
        P = P->link;
    }
    printf("\n");
}

程序的输出要求 : 系数指数空格 (如下图)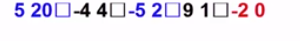
(最后一项没有空格)