堆栈是什么

  • 一种特殊的线性表** **, 函数调用、递归、表达式求值都需要用到堆栈

例1 表达式求值

算术表达式二 : 线性结构 - (2)堆栈 - 图1

  • 算术表达式由数和运算符号构成
  • 不同运算符号优先级不一样

表达式根据运算符号的位置分类 :

  • 中缀表达式 : 符号位于数之间 , 如 a + b * c - d / e
  • 后缀表达式 : 符号位于数之后 , 如 a b c * + d e / -

上述两个表达式等价

  • 前缀表达式 : 符号位于数之前 , 如 - + a * b c / d e

后缀表达式例题 : 6 2 / 3 - 4 2 * + =?
解 :
① 62/ ——- 结果为 3 , 后续为 33-
② 33- ——- 结果为 0 , 后续为 042+
③ **042+** ——- 结果为 08+ , 结果为 8

后缀表达式求值策略 : 从左向右扫描 , 逐个处理运算数和符号 **（每个运算符消掉前面出现的两个数字）**

  • 如何记住目前不参与运算的数 ?
  • 运算符号对应的运算数是什么 ?

——— 结论 : 需要有种存储方法 , 能顺序存储运算数 , 并在需要时倒序输出 ——
( 即该种数据结构的特点应为 : 先进后出 , 后进先出)

堆栈的抽象数据类型描述

Stack（堆栈/栈）: 具有一定操作约束的线性表 , 只能在一端 (栈顶 , Top) 做插入、删除

  • 插入数据 : 入栈 (Push)
  • 删除数据 : 出栈 (Pop)
  • 后入先出 : Last In First Out ( LIFO )

操作集

  1. Stack CreateStack( int MaxSize ) : 生成空堆栈 , 其最大长度为 MaxSize
  2. int IsFull( Stack S, int MaxSize) : 判断堆栈S是否已满
  3. void Push( Stack S, ElementType item) : 将元素item压入堆栈
  4. int IsEmpty( Stack S ) : 判断堆栈S是否为空
  5. ElementType Pop( Stack S ) : 删除并返回堆栈元素


Push 和 Pop : **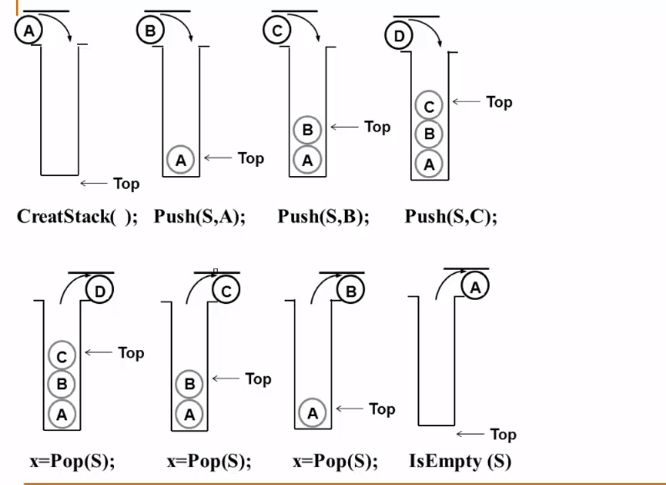
image.png

Push 和 Pop 可以穿插交替进行 , 顺序不同输出的序列顺序也不同

  • 输出 CBA , ACB 是可能的 , 输出 CAB 是不可能的

栈的顺序存储实现 (数组)

栈的顺序存储结构通常由一个一维数组和一个记录栈顶元素位置的变量组成
定义 : 

  1. #define MaxSize <储存数据元素的最大个数>
  2. typedef struct SNode *Stack;
  3. struct SNode{
  4.     ElementType Data[MaxSize];
  5.     int Top; #
  6. };

(1) 入栈 : 需要先判断栈是否满 (数组表示)

  1. void Push(Stack PtrS, ElementType item){
  2.     if( PtrS->Top == MaxSize-1){
  3.         printf("堆栈满");return;
  4.     }else{
  5.         PtrS -> Data[++(PtrS->Top)] = item;return; /*item放在Top上面的位置,所以是++*/
  6.     }
  7. }

(2) 出栈 : 先判断栈是否是空

  1. ElementType Pop(Stack PtrS){
  2.     if(PtrS->Top == -1){
  3.         printf("堆栈空");return ERROR; /*ERROR是ElementType的特殊值,标志错误*/
  4.     }else{
  5.         return (PtrS->Data[(PtrS->Top)--]);
  6.     }
  7. }

例题

用一个数组实现两个堆栈 , 要求最大化地利用数组空间 , 使数组只要有空间入栈操作就可以成功
(只要某一个数组有空余空间就允许有入栈操作)
【分析】使这两个栈分别从数组的两头开始向中间生长 ; 当两个栈的栈顶指针相遇时 , 代表两个栈都满了
定义 : 

  1. #define MaxSize<存储数据元素的最大个数>
  2. struct DStack{
  3.     ElementType Data[MaxSize];
  4.     int Top1;    /*堆栈1的栈顶指针*/
  5.     int Top2;    /*堆栈2的栈顶指针*/
  6. }S;
  7. /*S.Top1 = -1*/
  8. /*S.Top2 = MaxSize*/

(1) 入栈Push : 

  1. void Push( struct DStack *PtrS, ElementType item, int Tag){
  2.     /*Tag作为区分两个堆栈的标志,取值为1和2*/
  3.     if(PtrS->Top2 - PtrS->Top1 == 1){ /*堆栈满*/
  4.         printf("堆栈满");return;
  5.     }
  6.     if(Tag == 1) /*对第一个堆栈操作*/
  7.         PtrS->Data[++(PtrS->Top1)] = item;
  8.     else
  9.         PtrS->Data[(Ptrs->Top2)--] = item;
  10. }

(2) 出栈Pop :

  1. ElementType Pop( struct DStack *PtrS, int Tag){
  2.     /*Tag作为区分两个堆栈的标志,取值为1和2*/
  3.     if( Tag == 1 ){
  4.         if( PtrS->Top1 == -1){    /*堆栈1空*/
  5.             printf("堆栈1空");return NULL;
  6.         }else return PtrS->Data[(PtrS->Top1)--];
  7.     }else{
  8.         if( PtrS->Top2 == MaxSize){    /*堆栈2空*/
  9.             printf("堆栈2空");return NULL;            
  10.         }else return PtrS->Data[(PtrS->Top2)++];
  11.     }
  12. }

栈的链式存储实现 (链表)

数组可以实现的话 , 一般用链表也可以实现
叫做链栈 , 插入和删除操作只能在链栈的栈顶进行。栈顶指针Top应该在链表的哪一头?哪一头作为Top?
链尾不能作为Top

定义 :

  1. typedef struct SNode *Stack;
  2. struct SNode{
  3.     ElementType Data;
  4.     struct SNode *Next;
  5. }

(1) 堆栈初始化 (建立空栈)
(2) 判断堆栈S是否为空

  1. Stack CreateStack(){
  2.     /*构建一个堆栈的头结点,返回指针*/
  3.     Stack S;
  4.     S = (Stack)malloc(sizeof(struct SNode));
  5.     S->Next = NULL;
  6.     return S;
  7. }
  9. int IsEmpty(Stack S){
  10.     /*判断堆栈S是否为空,若为空则返回整数1,否则返回0*/
  11.     return ( S->Next == NULL );
  12. }

实际上得到这样一种结构 : 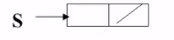image.png
(3) 入栈Push : (插入到链表的头)

  1. void Push( ElementType item, Stack S){
  2.     /*将元素item压入堆栈S*/
  3.     struct SNode *TmpCell;
  4.     TmpCell = (struct SNode *)malloc(sizeof(struct SNode));
  5.     TmpCell->Element = item;
  6.     TmpCell->Next = S->Next;
  7.     S->Next = TmpCell;
  8. }

(4) Pop操作类似 , 需要先判断堆栈是否是空 (删除操作)

  1. ElementType Pop(Stack S){
  2.     /*删除并返回堆栈S的栈顶元素*/
  3.     struct SNode *FirstCell;
  4.     ElementType TopElem;
  5.     if( IsEmpty(S)){
  6.         printf("堆栈空");return NULL;
  7.     }else{
  8.         FirstCell = S->Next;  /*先赋值*/
  9.         S->Next = FirstCell->Next;
  10.         TopElem = FirstCell->Element;
  11.         free(FirstCell);  /*再释放空间*/
  12.         return TopElem;
  13.     }
  14. }

为什么在Push的时候不判断堆栈满不满?

因为用数组实现时大小固定 , 存在堆栈满不满的问题 , 而链表不是一次性申请大段内存 , 而是不断地申请小块内存 , 所以不需要判别满不满

应用 : 表达式求值

回过头来解决表达式求值的问题

后缀表达式求值 (简单)

应用堆栈实现后缀表达式求值的基本过程 : 从左到右读入后缀表达式的各项 (运算符或运算数)

  • 运算数 : 入栈
  • 运算符 : 从堆栈中弹出适当数量的运算数 , 计算出结果出栈 ;
  • 最后栈顶上的元素就是表达式的结果值

中缀表达式求值 (中等)

策略 : 将中缀表达式转化为后缀表达式然后求值
例 : 二 : 线性结构 - (2)堆栈 - 图4
数的相对顺序不变 , 但运算符号顺序发生改变 , 这意味着 :

  • 需要存储”等待中”的运算符号
  • 需要将当前运算符号与”等待中”的最后一个运算符号比较优先级

碰到运算数直接输出 , 碰到运算符号先储存 , 到下一个运算符号时与前一个比较再判断优先级
**

有括号的中缀表达式求值 (难)

例 : 二 : 线性结构 - (2)堆栈 - 图5
堆栈中只存储运算符 , (左括号的优先级比乘号高 , 比后续的符号低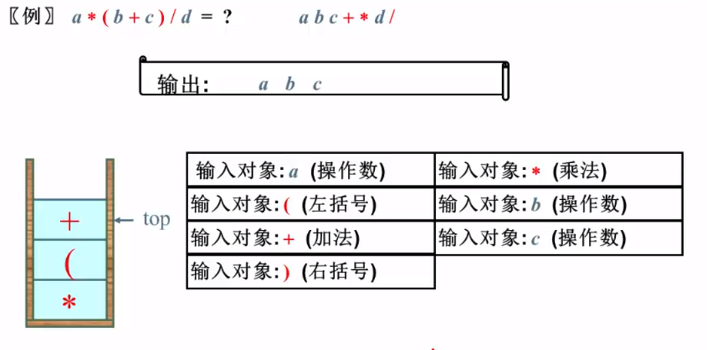
image.png此时抛出+号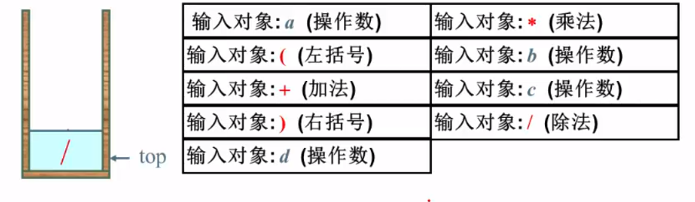
image.png
**相同优先级从左到右运算 (此处号出栈/号进栈)

时间复杂度为线性 : 二 : 线性结构 - (2)堆栈 - 图8

例题 : 将中缀表达式 二 : 线性结构 - (2)堆栈 - 图9转化为后缀表达式 , 在这个转换过程中 , 堆栈元素最多时的元素个数是 ? (3个)

把中缀转化为后缀

▷ 从头到尾读取中缀表达式的每个对象 , 对不同对象按不同的情况处理

  1. 运算数 : 直接输出
  2. 左括号 : 压入堆栈
  3. 右括号 : 将栈顶的运算符弹出并输出 , 直到遇到左括号(出栈 , 不输出)
  4. 运算符 :
    a. 若优先级大于栈顶运算符时 , 把它压栈 ;
    b. 若优先级小于栈顶运算符时 , 将栈顶运算符弹出并输出 ; 再比较新的栈顶运算符 , 直到该运算符大于栈顶运 算符优先级位置 , 然后将该运算符压栈
  5. 若各对象处理完毕 , 则把堆栈中存留的运算符一并输出

上述例题 :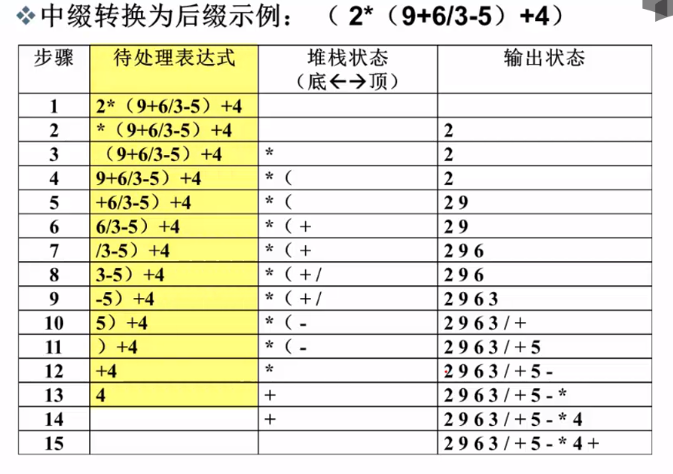
image.png

堆栈的其他应用

  • 函数调用及递归实现 :
    函数A里调用函数B , 函数B里调用函数C… 需要按倒过来的顺序返回到函数B再返回到函数A
  • 深度优先搜索
  • 回溯算法 : 试探各种可能性 , 走不通时需要返回到上一个路口
  • …

小测验

image.png

课件

2.2堆栈.pdf

C语言实现 : 堆栈的定义和操作(顺序存储)

  1. typedef int Position;
  2. struct SNode {
  3.     ElementType *Data; /* 存储元素的数组 */
  4.     Position Top;      /* 栈顶指针 */
  5.     int MaxSize;       /* 堆栈最大容量 */
  6. };
  7. typedef struct SNode *Stack;
  9. Stack CreateStack( int MaxSize )
  10. {
  11.     Stack S = (Stack)malloc(sizeof(struct SNode));
  12.     S->Data = (ElementType *)malloc(MaxSize * sizeof(ElementType));
  13.     S->Top = -1;
  14.     S->MaxSize = MaxSize;
  15.     return S;
  16. }
  18. bool IsFull( Stack S )
  19. {
  20.     return (S->Top == S->MaxSize-1);
  21. }
  23. bool Push( Stack S, ElementType X )
  24. {
  25.     if ( IsFull(S) ) {
  26.         printf("堆栈满");
  27.         return false;
  28.     }
  29.     else {
  30.         S->Data[++(S->Top)] = X;
  31.         return true;
  32.     }
  33. }
  35. bool IsEmpty( Stack S )
  36. {
  37.     return (S->Top == -1);
  38. }
  40. ElementType Pop( Stack S )
  41. {
  42.     if ( IsEmpty(S) ) {
  43.         printf("堆栈空");
  44.         return ERROR; /* ERROR是ElementType的特殊值，标志错误 */
  45.     }
  46.     else 
  47.         return ( S->Data[(S->Top)--] );
  48. }

C语言实现 : 堆栈的定义和操作(链式存储)

  1. typedef struct SNode *PtrToSNode;
  2. struct SNode {
  3.     ElementType Data;
  4.     PtrToSNode Next;
  5. };
  6. typedef PtrToSNode Stack;
  8. Stack CreateStack( ) 
  9. { /* 构建一个堆栈的头结点，返回该结点指针 */
  10.     Stack S;
  12.     S = (Stack)malloc(sizeof(struct SNode));
  13.     S->Next = NULL;
  14.     return S;
  15. }
  17. bool IsEmpty ( Stack S )
  18. { /* 判断堆栈S是否为空，若是返回true；否则返回false */
  19.     return ( S->Next == NULL );
  20. }
  22. bool Push( Stack S, ElementType X )
  23. { /* 将元素X压入堆栈S */
  24.     PtrToSNode TmpCell;
  26.     TmpCell = (PtrToSNode)malloc(sizeof(struct SNode));
  27.     TmpCell->Data = X;
  28.     TmpCell->Next = S->Next;
  29.     S->Next = TmpCell;
  30.     return true;
  31. }
  33. ElementType Pop( Stack S )  
  34. { /* 删除并返回堆栈S的栈顶元素 */
  35.     PtrToSNode FirstCell;
  36.     ElementType TopElem;
  38.     if( IsEmpty(S) ) {
  39.         printf("堆栈空"); 
  40.         return ERROR;
  41.     }
  42.     else {
  43.         FirstCell = S->Next; 
  44.         TopElem = FirstCell->Data;
  45.         S->Next = FirstCell->Next;
  46.         free(FirstCell);
  47.         return TopElem;
  48.     }
  49. }