集合的表示

※ 集合运算 : 交 , 并 , 补 , 差 , 判定某元素是否属于某集合
※ 并查集 : 集合并 , 查某元素属于什么集合

例题

有10台电脑 {1, 2, 3,……, 9, 10} , 已知下列电脑之间已经实现了连接 : 1和2 , 2和4 , 3和5 , 4和7 , 5和8 , 6和9 , 6和10 问 : 2和7之间 , 5和9之间是否是连通的?

解决思路

(1) 将10台电脑看成10个集合 {1} , {2} , {3} ,……, {9} , {10}
(2) 已知一种连接 “x和y” , 就将x和y对应的集合合并
(3) 查询 “a和b是否是连通的” , 就是判别a和b是否同属于一个集合

操作

(1) 合并两个集合
(2) 查询某元素是否属于某集合

并查集存储实现

并查集问题中集合存储如何实现 ?

※ 可以用树结构表示集合 , 树的每个结点代表一个集合元素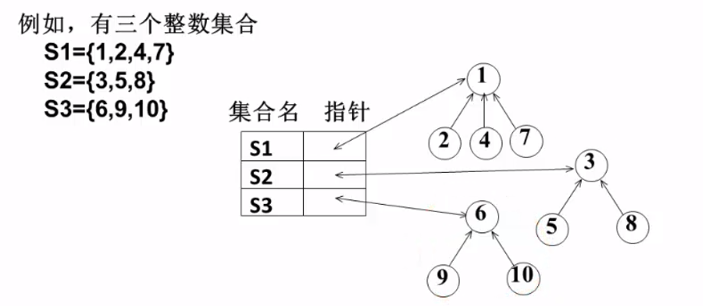
image.png
双亲表示法 : 孩子指向父亲
用链表存储还是用数组存储 ? —— 用数组更好

用数组存储并查集

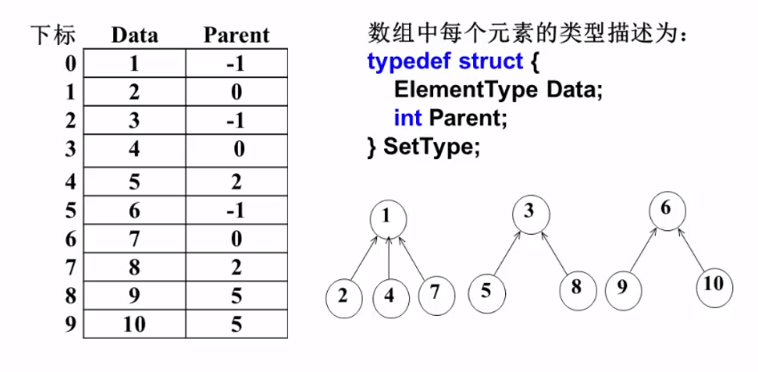
image.png
Parent 表示该结点的父结点下标 , 若该结点是根结点 , 没有父亲 , 则Parent下标为 -1

查找操作

查找某个元素所在的集合

  1. int Find(SetType S[ ], ElementType X){
  2.     /*在数组S中查找值为X的元素所属的集合*/
  3.     /*MaxSize是全局变量,为数组S的最大长度*/
  4.     int i;
  5.     for(i=0 ; i < MaxSize && S[i].Data != X ; i++);
  6.     if( i >= MaxSize ) return -1;    /*没找到X则返回-1*/
  7.     for(; S[i].Parent >= 0 ; i = S[i].Parent);
  8.     return i;    /*找到X所属集合,返回树根结点在数组S中的下标*/
  9. }

并运算

将两个已知元素X1, X2的所属集合合并成一个集合

(1) 分别找到X1和X2两个元素所在集合树的根结点
(2) 如果他们不同根 , 则将其中一个根结点的父结点指针设置成另一个根结点的数组下标

void Union (SetType S[], ElementType X1, ElementType X2){
    int Root1, Root2;
    Root1 = Find(S,X1);    /*根据Find函数找到X1所在树(集合)的根结点Root1*/
    Root2 = Find(S,X2); /*根据Find函数找到X2所在树(集合)的根结点Root2*/
    if(Root1 != Root2)    S[Root2].Parent = Root1;    /*将Root2指向Root1*/
}

对下图中的 2和5 进行并运算 :
(1) 通过 2 找到根结点 1(Root1) , 通过 5 找到根结点 3(Root2)
(2) 将 3 指向 1 /将Root2指向Root1/
(3) 修改 3 的指针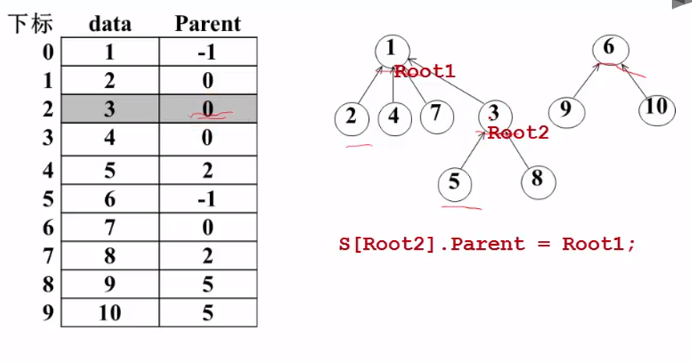
image.png
为了改善合并以后的查找性能 , 可以采用小的集合合并到相对大的集合中 (修改Union函数)

  • 为了避免一味增加树的高度 , 提升因合并而已经降低的效率

方法 :
将根结点的Parent指针 (-1) 改为负号和表示集合元素的个数的数字 , 比如上图

  • 1 的 Parent指针 -1 改成 - 7 (表示是有7个元素的根结点)
  • 6 的 Parent指针 -1 改成 - 3 (表示是有3个元素的根结点)

这样可以不用多申请额外的空间来比较集合大小

讨论 : 如何让并查树更矮 ?

Union 为了改善合并以后的查找性能，可以采用小的集合合并到相对大的集合中
将小集合中的child全部指向大集合的parent node

课件

5.3 集合及运算.pdf

C语言实现 : 集合的定义与并查

#define MAXN 1000                  /* 集合最大元素个数 */
typedef int ElementType;           /* 默认元素可以用非负整数表示 */
typedef int SetName;               /* 默认用根结点的下标作为集合名称 */
typedef ElementType SetType[MAXN]; /* 假设集合元素下标从0开始 */

void Union( SetType S, SetName Root1, SetName Root2 )
{ /* 这里默认Root1和Root2是不同集合的根结点 */
    /* 保证小集合并入大集合 */
    if ( S[Root2] < S[Root1] ) { /* 如果集合2比较大 */
        S[Root2] += S[Root1];     /* 集合1并入集合2  */
        S[Root1] = Root2;
    }
    else {                         /* 如果集合1比较大 */
        S[Root1] += S[Root2];     /* 集合2并入集合1  */
        S[Root2] = Root1;
    }
}

SetName Find( SetType S, ElementType X )
{ /* 默认集合元素全部初始化为-1 */
    if ( S[X] < 0 ) /* 找到集合的根 */
        return X;
    else
        return S[X] = Find( S, S[X] ); /* 路径压缩 */
}