红黑树
为什么不用AVL(二叉平衡树)?
因为AVL的实现比较复杂,算法也复杂度也高、因此我们使用红黑树。
红黑树的特点
- 插入和查询的复杂度是O(logn)
- 不是完全平衡的;
红黑树的定义
- 结点要么红色要么黑色
- 根节点是黑色的
- 每个叶子节点(指的是null)是黑色的;
- 如果一个结点是红色的,那么它的两个儿子都是黑色的;
- 对每个结点,从该结点出发到其任意叶子节点的简单路径上包含相同数目的黑结点。
红黑树的生成
- 每个插入的结点是红色;
- 检查是否满足红黑树的定义,如果不满足,就需要变色 + 旋转使其满足红黑色的定义;
- 有时候只需要变色就可以满足红黑色的定义。
红黑树的优点
- 相比于AVL树,插入和删除时只需要更少的旋转,因此插入删除效率比AVL树更高。
- 查询效率比AVL树略低,但是低的不多。
- 因此综合起来,红黑树性能均衡。当插入删除的操作较多时,性能要强于AVL树。
如何扩容?
- 生成新数组,数组长度为老数组的双倍;
- 遍历旧数组,如果只有一个元素,直接用hash值得到新的index,转移到新数组;
- 如果是链表,则让hash值与长度按位与,得到的结果要么为0,要么不为0, 如下: ```bash 1010 0011 1011 0011 0001 0000 0001 0000 &
0000 0000 0001 0000
- 如果为0,就将为0的结点组合成一个链表,移动到原来的index上;- 如果不为0,就将不为0的结点组合成一个链表,移动到index + oldLength的结点上;4. 如果是红黑树:- 如果只能拆成一个链表,那么说明仍然是树,把树移过去即可- 如果能拆成两个链表,且链表长度比阈值小,那么就保留为链表,否则树化。<a name="CKckS"></a># 与1.7的差异1. 添加了红黑树,当链表长度大于阈值(默认为8, 即最多能放8个,当放第9个的时候转化为红黑树),调用树化方法,但是不一定就转化成红黑树。在树化方法里,判断了如果数组长度小于64时的时候,只会去给数组扩容,大于64才会采取树化;```javafinal void treeifyBin(Node<K,V>[] tab, int hash) {int n, index; Node<K,V> e;// 数组长度小于64时,做resize而不是树化。if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)resize();else if ((e = tab[index = (n - 1) & hash]) != null) {TreeNode<K,V> hd = null, tl = null;do {TreeNode<K,V> p = replacementTreeNode(e, null);if (tl == null)hd = p;else {p.prev = tl;tl.next = p;}tl = p;} while ((e = e.next) != null);if ((tab[index] = hd) != null)hd.treeify(tab);}}
- 1.8采用了尾插法,而1.7采用的是头插法;
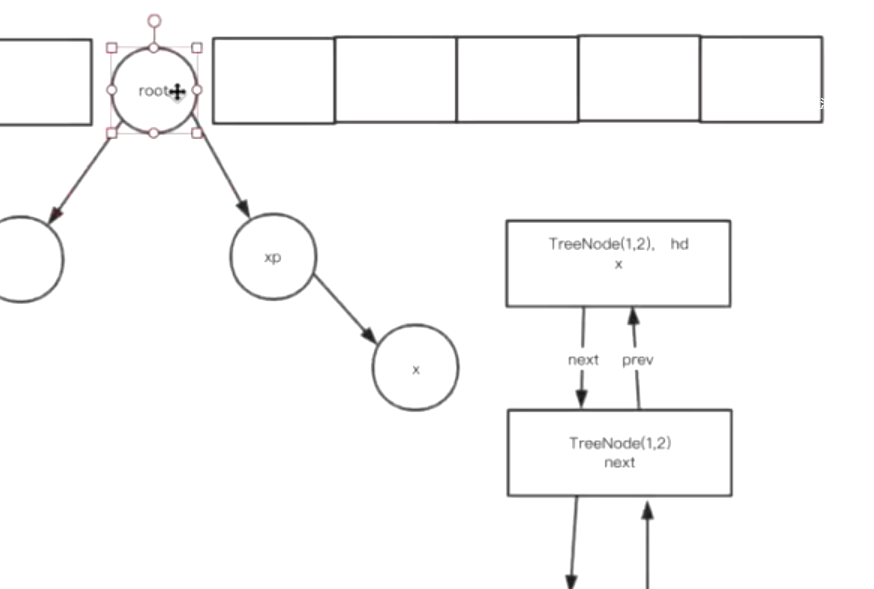
1.8中,如果转化成了红黑树,那么一个Node就会变成TreeNode, 注意TreeNode同时有left和right用来形成红黑树,也有pre和next用来组成双向链表。转化结束后,会把红黑树的根结点变成双向链表的第一个结点,以方便操作。
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {TreeNode<K,V> parent; // red-black tree linksTreeNode<K,V> left;TreeNode<K,V> right;TreeNode<K,V> prev; // needed to unlink next upon deletionboolean red;TreeNode(int hash, K key, V val, Node<K,V> next) {super(hash, key, val, next);}...}
1.7的扩容条件有两个:
- size >= threshold
- null != table[bucketIndex]
即,首先要size比阈值要大,其次是要放的那个index的位置上是有结点的。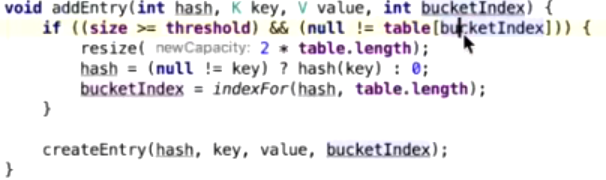
1.8的扩容则去掉了第二个条件。
1.7在扩容时,挨个算,挨个转移;
1.8在扩容时,算了以后先组成链表,然后统一进行转移;
源码
putVal方法
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
// 如果数组没有初始化,就去初始化数组
if ((tab = table) == null || (n = tab.length) == 0)
// resize方法有两个功能,一是扩容,二是初始化
n = (tab = resize()).length;
// 如果要放的位置上没有其他结点
if ((p = tab[i = (n - 1) & hash]) == null)
// 直接放入
tab[i] = newNode(hash, key, value, null);
// 如果要放的位置存在其他结点
else {
Node<K,V> e; K k;
// 如果第一个位置上的结点和我们要放入的结点的key是相同的,那么就让e指向该结点
// 在后面把p的值进行覆盖
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
// 如果是一棵树
else if (p instanceof TreeNode)
// 就把结点放进树里
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
// 如果是一个链表
else {
// 遍历链表
for (int binCount = 0; ; ++binCount) {
// 如果遍历到了结尾
if ((e = p.next) == null) {
// 尾插法,1.7中采用头插法
p.next = newNode(hash, key, value, null);
//如果链表里的结点数足够多了,进行树化
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
// 如果在遍历的过程中,找到了相同的key,
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
// 让p往下遍历而已,可以画一下链表的结构
p = e;
}
}
// 在三种情况下,都可能能找到键相同的结点,那么就进行覆盖
// 此时e结点必定不为null
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
// 如果结点数很多了,进行resize
if (++size > threshold)
resize();
// 插入后的操作
afterNodeInsertion(evict);
return null;
}
Resize方法
初始化数组或者扩容
final Node<K,V>[] resize() {
// 老数组和老数组的一些属性
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
// 新容量和新的阈值
int newCap, newThr = 0;
// 说明老数组不为空
if (oldCap > 0) {
// 如果已经达到了最大值,就设置成整数的最大值
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
// 新的数组长度为老数组的两倍
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
// 新的阈值等于老阈值的两倍
newThr = oldThr << 1; // double threshold
}
// 这里的判断不懂
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
// 没有被初始化过,那么就赋初值
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
// 如果新的阈值为0,就是计算新阈值,仍然是cap * loadFactor
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
// 阈值的赋值
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
// new出新数组
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
// 如果老数组不为空,进行扩容
if (oldTab != null) {
// 遍历老数组
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
// 如果链表上是有值的
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
//如果只有一个值,直接复制到新数组即可
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
// 如果是一棵树,对树进行拆分
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
// 那么就是一个链表了
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
// 遍历整个链表,根据新下标拆成两个链表
do {
next = e.next;
// 第一个链表,其新下标不变
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
// 第二个链表,新下标为旧下标 + oldLength
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
// 将第一个链表移过去
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
// 将第二个链表移过去
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}

