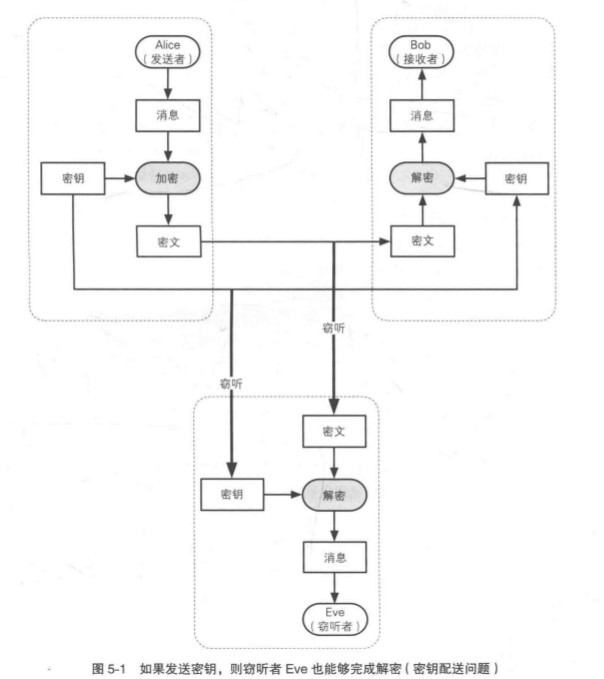
秘钥配送问题

当我们使用对称密码时，我们一定会遇到 密钥配送问题。
image.png

如何解决密钥配送问题？

通过事先共享密钥来解决

image.png

通过密钥分配中心来解决

建立在上一个解决方案的基础上，提出了进一步的解决方案，通过密钥分配中心（Key Distribution Center,KDC）来解决问题。
image.png
但是如果KDC被攻破，攻击者可以获取全部人的通信内容

通过Diffie-Hellman 密钥交换来解决

后面补坑

通过公钥密码来解决

image.png

什么是公钥密码

公钥密码（public-key cryptography）中，密钥分为加密秘钥和解密秘钥两种。发送者用加密秘钥对消息进行加密，接受者用解密秘钥对密文进行解密。
image.png
image.png

通信过程

假设Alice要给Bob发消息。在公钥密码通信中，通信过程是由Bob来启动的。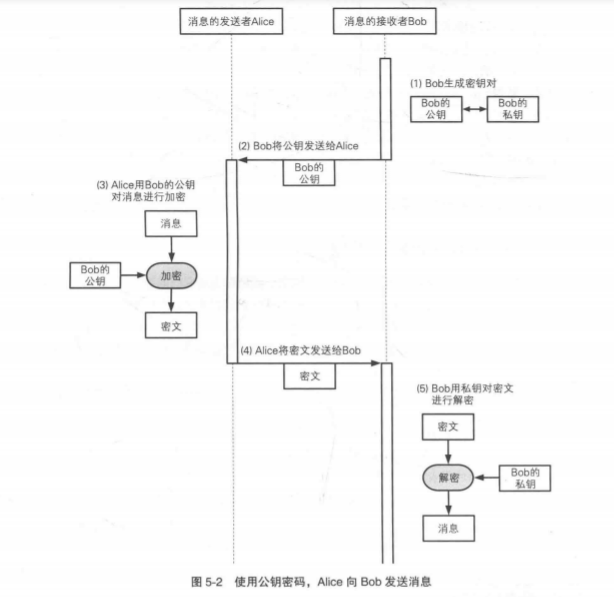
image.png

公钥密码中的术语

image.png

公钥密码无法解决的问题

公钥密码解决了密钥配送的问题，但不意味着他能够解决所有的问题。因为无法判断公钥是否合法。这个问题被称为公钥认证问题。

时钟运算

这里涉及到比较长的篇幅，设计离散对数等相关内容，有需要的伙伴可以去参考图解密码技术，我就不在此赘述了。

RSA

什么是RSA

RSA是一种公钥密码算法
RSA 可以被用于公钥密码和数字签名。

RSA加密

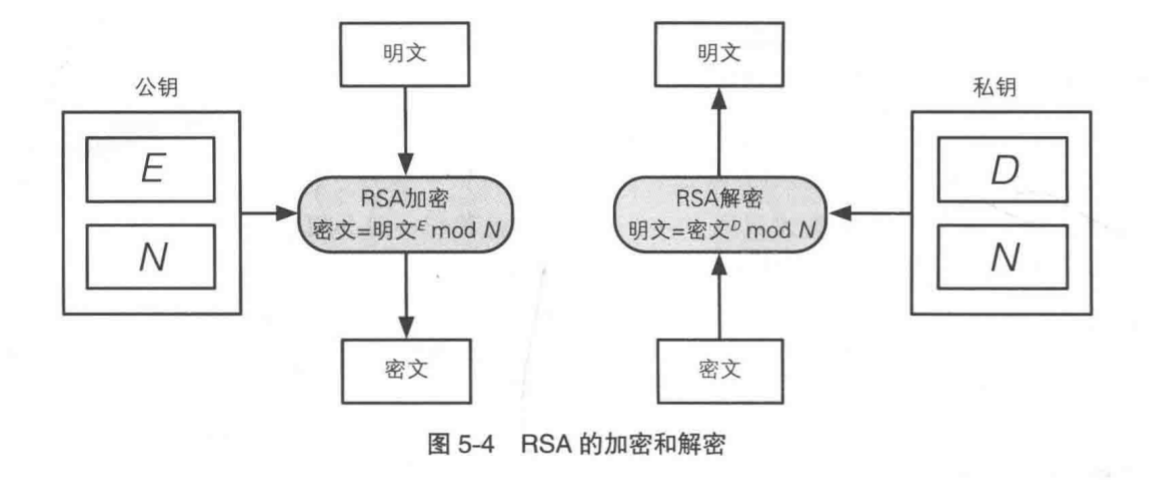
在RSA中，明文、密钥、和密文都是数字。RSA的加密过程可以用以下公式来表达
密文 = 明文 ^ E mod N (RSA 加密)
image.png
RSA密文是代表明文的数字的 E次方 求 mod N 的结果。
人话：
将 明文 做 E次乘法，然后将其结果除以 N。
这个公式中出现了两个数 E 和 N。
E 和 N 是 RSA 加密的密钥，E 和 N 的组合就是公钥。
不过E 和 N 不是随便什么数都可以的，它们是经过严格的计算得出的。
E（encryption） N (number)
一般来说用 ‘公钥是（E,N）’的形式来表达

RSA解密

明文 = 密文 ^ D mod N
image.png
对 密文 的 D 次方 求 mod N 就可以得到明文
这里的 N 是和加密的时候使用的 N相同的。
数 D 和 数 N 的组合就是私钥
D（decryption） N (number)
image.png
image.png