树

定义

A tree is a (possibly non-linear) data structure made up of nodes or vertices and edges without having any cycle. The tree with no nodes is called the null or empty tree. A tree that is not empty consists of a root node and potentially many levels of additional nodes that form a hierarchy.

树是由结点或顶点和边组成的(可能是非线性的)且不存在着任何环的一种数据结构。没有结点的树称为空(null或empty)树。一棵非空的树包括一个根结点，还(很可能)有多个附加结点，所有结点构成一个多级分层结构。

基本称呼

Root	The top node in a tree.	根	树的顶端结点
Child	A node directly connected to another node when moving away from the Root.	孩子	当远离根(Root)的时候，直接连接到另外一个结点的结点被称之为孩子(Child);
Parent	The converse notion of a child.	双亲	相应地，另外一个结点称为孩子(child)的双亲(parent)。
Siblings	A group of nodes with the same parent.	兄弟	具有同一个双亲(Parent)的孩子(Child)之间互称为兄弟(Sibling)。
Ancestor	A node reachable by repeated proceeding from child to parent.	祖先	结点的祖先(Ancestor)是从根（Root）到该结点所经分支(Branch)上的所有结点。
Descendant	A node reachable by repeated proceeding from parent to child.	子孙	以某结点为根的子树中的任一结点都称为该结点的子孙(后代)。
Leaf	A node with no children.	叶子（终端结点）	没有孩子的结点(也就是度为0的结点)称为叶子(Leaf)或终端结点。
Branch	A node with at least one child.	分支(非终端结点)	至少有一个孩子的结点称为分支(Branch)或非终端结点。
Degree	The number of sub trees of a node.	度	结点所拥有的子树个数称为结点的度(Degree)。（跟图的度不太一样）
Edge	The connection between one node and another.	边	一个结点和另一个结点之间的连接被称之为边(Edge)。
Path	A sequence of nodes and edges connecting a node with a descendant.	路径	连接结点和其后代的结点之间的(结点,边)的序列。
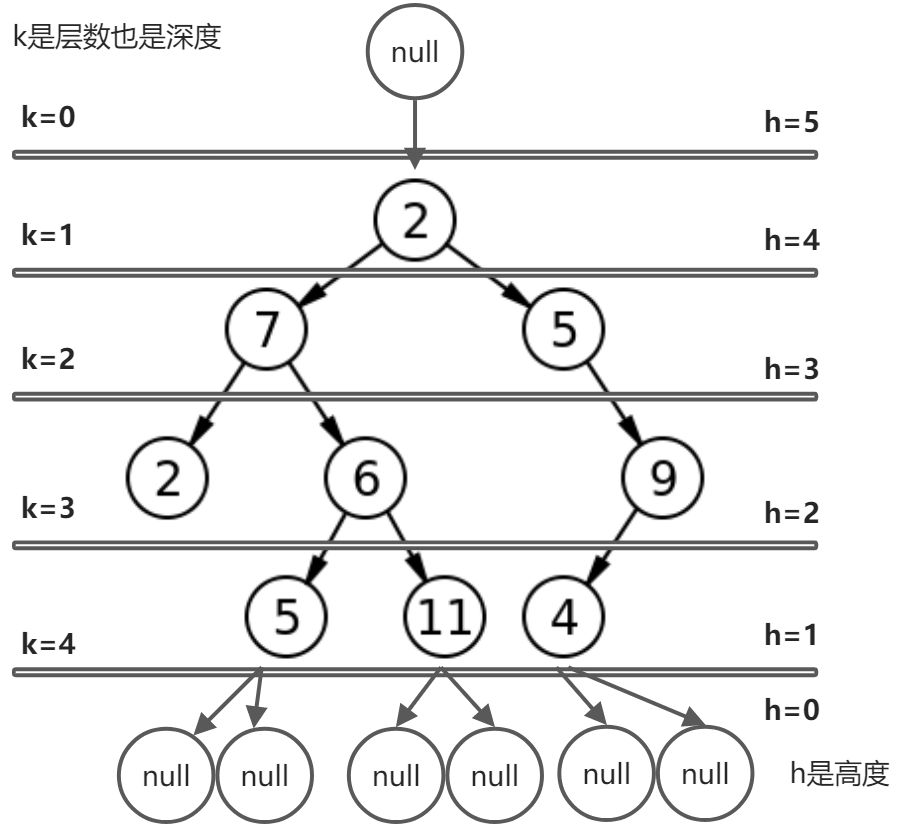
Level	The level of a node is defined by ０ + (the number of connections between the node and the root).	层次	结点的层次(Level)从根(Root)开始定义起，根为第0层，根的孩子为第1层。以此类推，若某结点在第i层，那么其子树的根就在第i+1层。
Height of node	The height of a node is the number of edges on the longest path between that node and a leaf.	结点的高度	结点的高度是该结点和某个叶子之间存在的最长路径上的边的个数。
Height of tree	The height of a tree is the height of its root node.	树的高度	树的高度是其根结点的高度。
**Depth of node

二叉树（Binary Tree）

二叉树 - 图1

定义

每个结点至多拥有两棵子树(即二叉树中不存在度大于2的结点)，
二叉树的子树有左右之分，其次序不能任意颠倒。

性质
若二叉树的层次从1开始，则在二叉树的第i层至多有2^（i-1）个结点(i>=1)。
高度为k的二叉树最多有2^k- 1个结点(k>=0)。 (空树的高度为0)
对任何一棵二叉树，如果其叶子结点(度为0)数为m, 度为2的结点数为n, 则m = n + 1。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。也就是最长叶子节点的k
分类
完美二叉树PBT / 满二叉树

一个深度为k(>=-1)
且有2^(k+1) - 1个结点

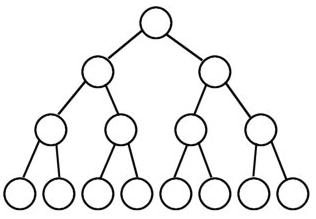
二叉树 - 图2

完全二叉树CBT

从根结点到倒数第二层满足完美二叉树，
最后一层可以不完全填充，其叶子结点都靠左对齐

换句话说，就是所有节点层序遍历编号连续。（一颗CBT就是从最右边取了几个元素的PBT）
二叉树 - 图3
优先级队列其实是一个堆，堆就是一棵完全二叉树，同时保证父子节点的顺序关系。

完满二叉树FBT

所有非叶子结点的度都是2。（只要你有孩子，你就必然是有两个孩子。）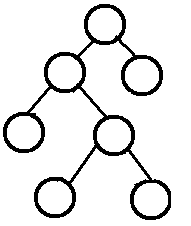
二叉树 - 图4

对比

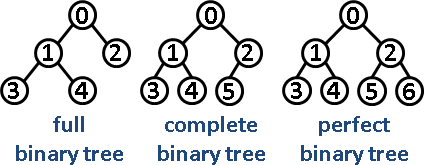
二叉树 - 图5
完满二叉树，完全二叉树，完美二叉树。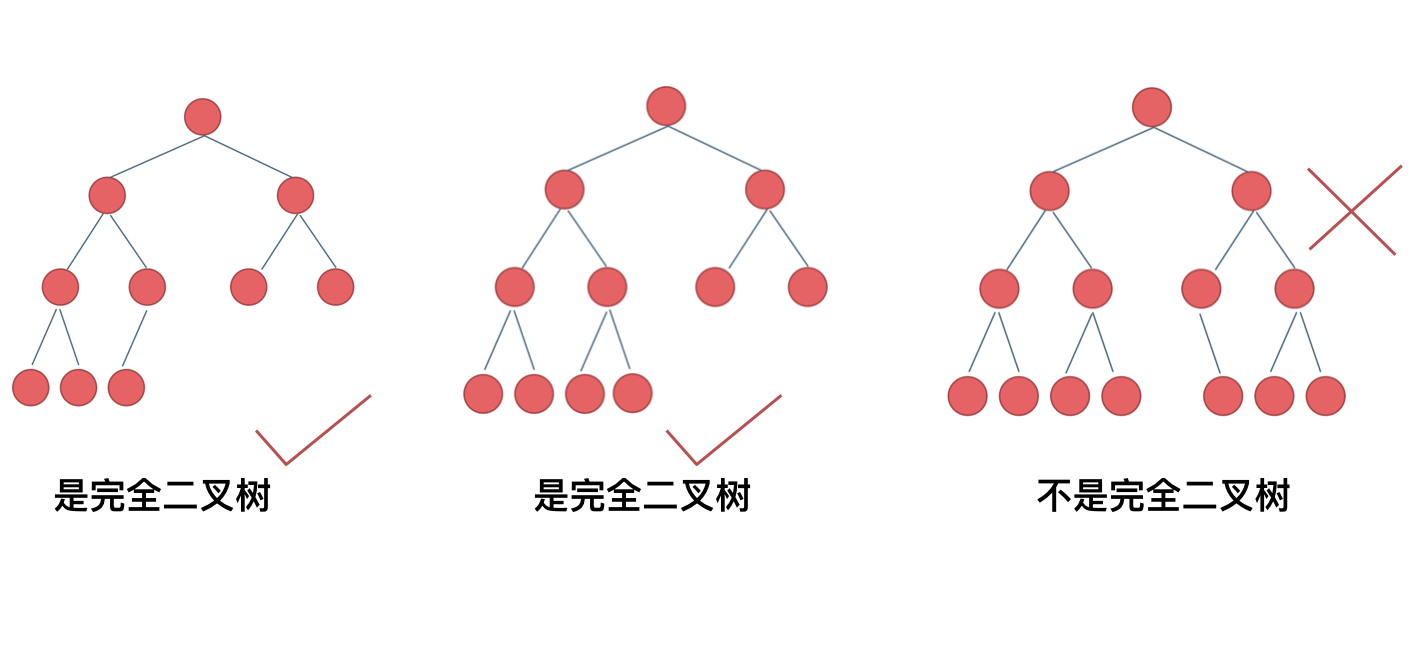

完美(Perfect)二叉树一定是完全(Complete)二叉树，但完全(Complete)二叉树不一定是完美(Perfect)二叉树。
完美(Perfect)二叉树一定是完满(Full)二叉树，但完满(Full)二叉树不一定是完美(Perfect)二叉树。
完全(Complete)二叉树可能是完满(Full)二叉树，完满(Full)二叉树也可能是完全(Complete)二叉树。
既是完全(Complete)二叉树又是完满(Full)二叉树也不一定就是完美(Perfect)二叉树。

二叉搜索树

有数值的二叉树二叉查找树，又名二叉排序树，亦名二叉搜索树

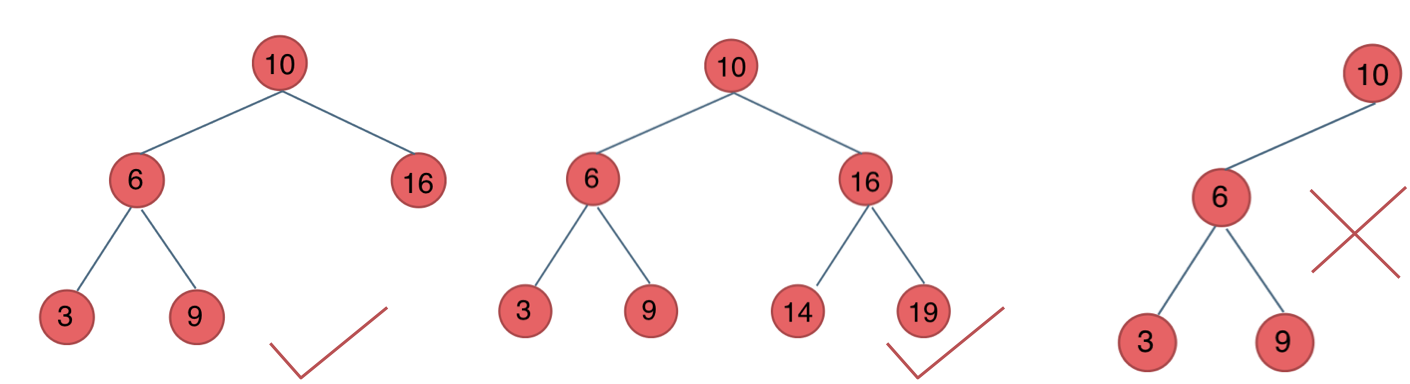
二叉搜索树是一个有序树：

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树
平衡二叉搜索树 AVL

又被称为AVL（Adelson-Velsky and Landis）树

性质：

它是一棵空树
或它的左右两个子树的高度差的绝对值不超过1，
- 并且左右两个子树都是一棵平衡二叉树。

:::info C++中map、set、multimap，multiset的底层实现都是平衡二叉搜索树，所以map、set的增删操作时间时间复杂度是logn
unordered_map、unordered_map底层实现是哈希表。 :::

红黑树

见此 https://www.cnblogs.com/skywang12345/p/3245399.html

二叉树的存储

链式

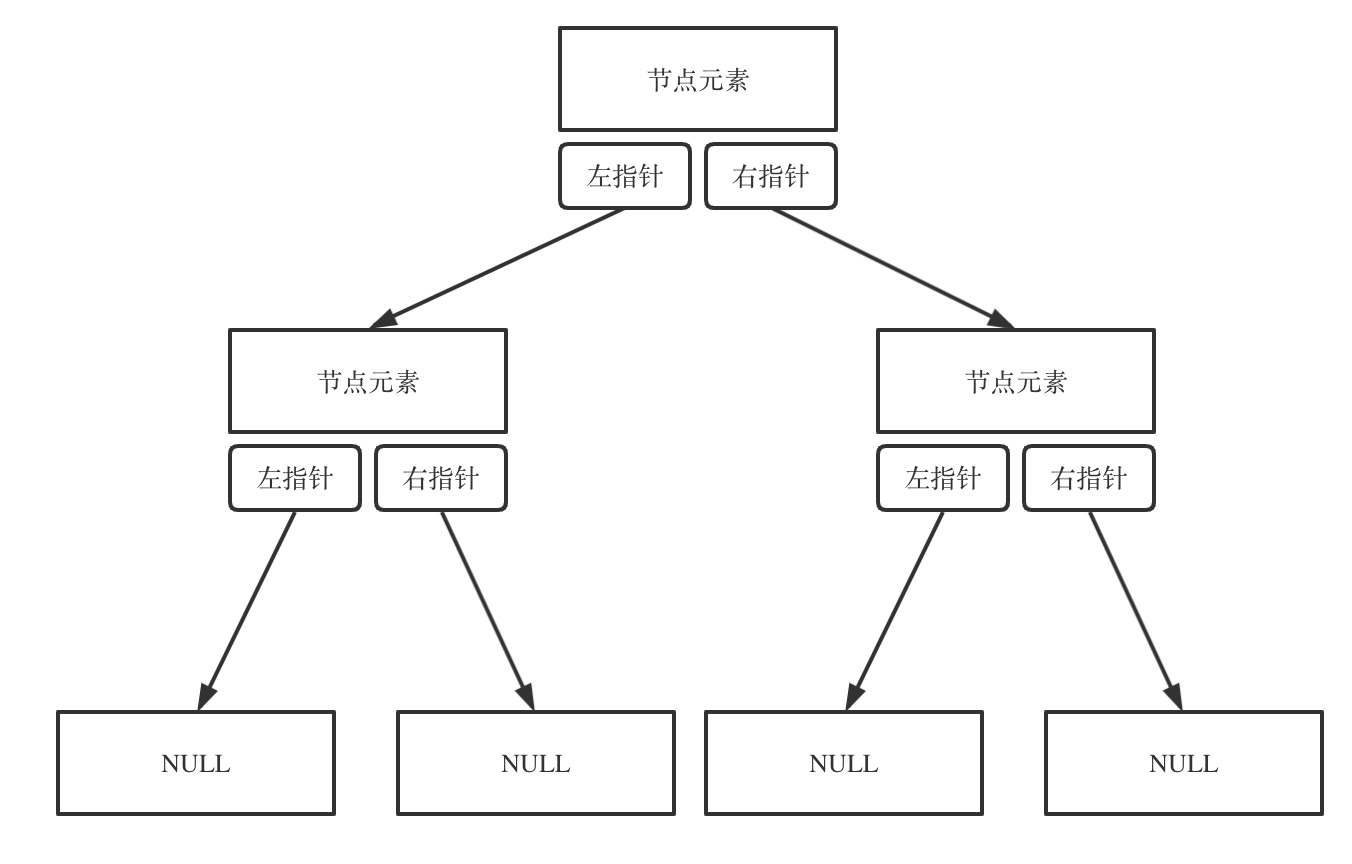
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

数组

如果父节点的数组下表是i，那么它的左孩子就是i * 2 + 1，右孩子就是 i * 2 + 2。

References：

https://www.cnblogs.com/idorax/p/6441043.html
https://programmercarl.com/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html#%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E7%A7%8D%E7%B1%BB

二叉树

树

定义